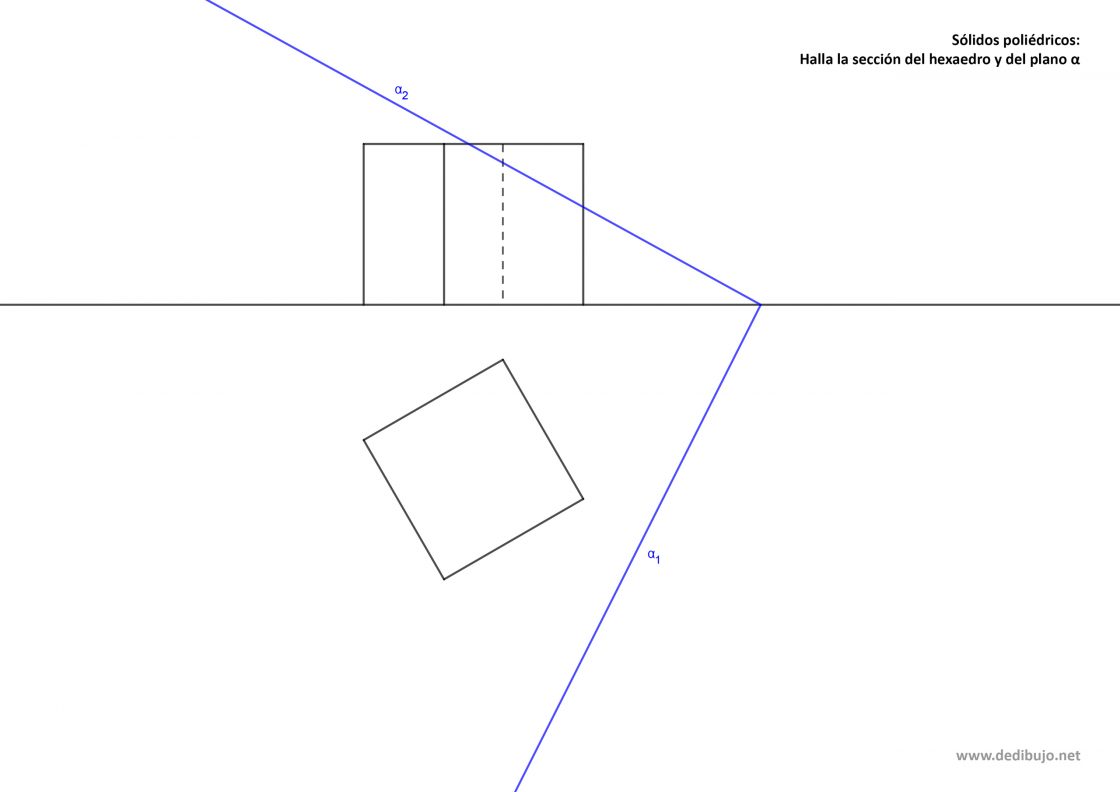
Hallar la sección que produce un plano oblicuo sobre un hexaedro regular es un ejercicio muy típico en segundo de bachillerato. Como datos iniciales te proporcionan un hexaedro, representado por sus proyecciones vertical y horizontal y un plano α representado por sus trazas vertical y horizontal. Tu punto de partida será algo parecido a esto:
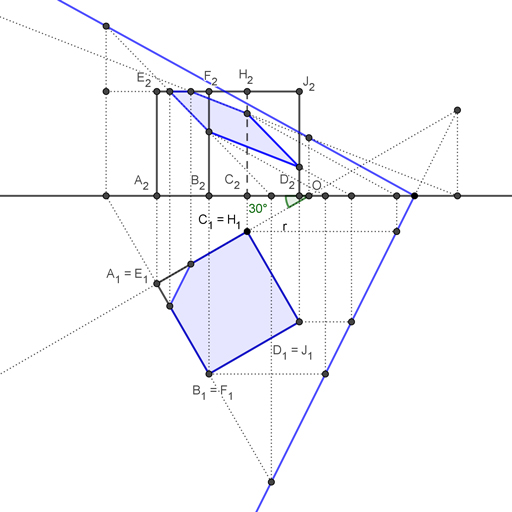
- Empieza por poner nombre a los puntos para poder identificarlos. Puedes mirar abajo la solución para ver como los he nombrado yo. Tras esto empezaremos hallando la intersección del segmento DJ con el plano α. Para hallar la intersección de una recta vertical con un plano oblicuo tienes que usar una recta frontal del plano.
- Traza una paralela a línea de tierra que pase por D1. Donde esa línea corta a la traza horizontal del plano tienes K1. Con una perpendicular a la línea de tierra hallar K2, y luego haces una paralela a la traza vertical del plano que pase por K2. Donde esa paralela corta al segmento que forman D2 y J2 tienes el punto L2, que es la intersección. Date cuenta que L1 coincide con D1.
- Repite el paso anterior para hallar las intersecciones de los segmentos BF y CH. Esos puntos de intersección puedes llamarlos M y N. Si intentas hallar la intersección del segmento AE con el plano, verás que no puedes porque se va por arriba. Eso significa que la intersección del plano se realiza sobre los segmentos EH y EF.
- La intersección del segmento EF es fácil. Incluye la recta en un plano proyectante horizontal. Halla la intersección de este plano, al que puedes llamar β con el plano α. Ese punto de intersección lo llamaremos P.
- Date cuenta de que tanto el segmento EF como el segmento EH tienen la misma altura. Eso significa que puedes hallar la intersección de ambos con el plano α usando una recta horizontal del plano que tenga esa misma altura. Así determinas tanto el punto P como el punto R al mismo tiempo.
Aquí abajo he incluido un método alternativo para hallar el punto R. Para ello he incluido el segmento EH en un plano proyectante horizontal. La parte complicada es que las trazas se cortan sobre el plano horizontal en un punto que tiene alejamiento negativo.
Otros tipos de secciones que te pueden interesar.
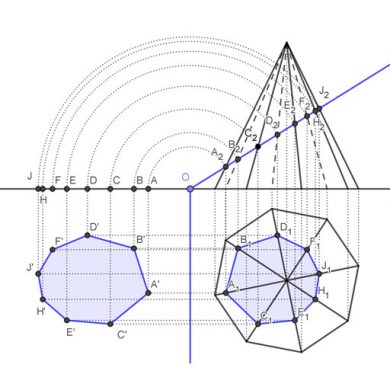
Sección plana de una pirámide de base octogonal con un plano proyectante vertical y verdadera magnitud
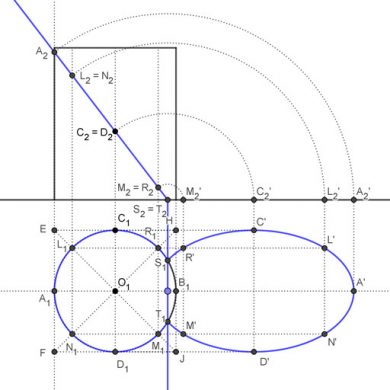
Sección plana de un cilindro con un plano proyectante vertical y su verdadera magnitud
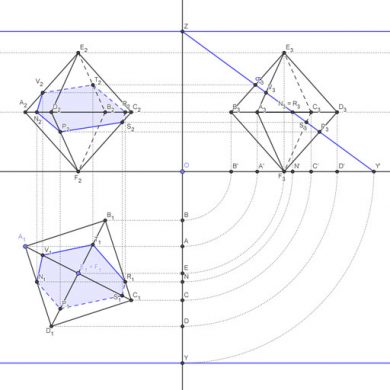
Sección plana de un octaedro por un plano paralelo a la línea de tierra
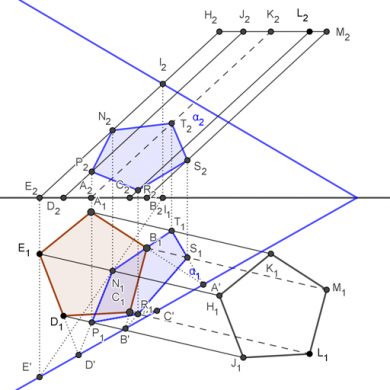
Sección plana de un prisma pentagonal oblicuo con un plano oblicuo en sistema diédrico
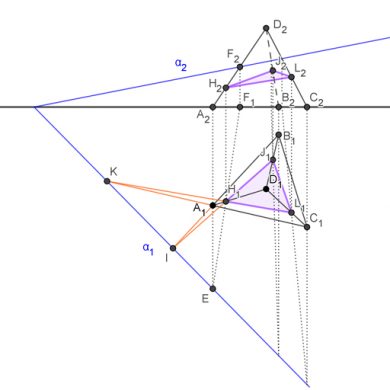
Sección plana de un tetraedro con un plano oblicuo
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.