El tema de la proporcionalidad y semejanza es básico para poder desarrollar construcciones mucho más complejas, como polígonos regulares o el trabajo con triángulos y cuadriláteros.
Razón y proporción
Antes de entrar en profundidad en el tema, hay determinados conceptos que debes conocer. Serían los siguientes:
Proporcionalidad
Se define como la relación existente entre las formas entre si, o con el conjunto. Sería la conformidad, correspondencia y equilibrio de las partes en un trabajo de dibujo u obra de arte.
Razón geométrica
Es la relación existente entre dos elementos (números, segmentos, etc.) Nos permite compararlos para saber cuantas veces es más grande (o pequeño) uno que otro. La razón geométrica de dos segmentos a y b se representa en forma de fracción a/b=k donde k es la razón geométrica que mantienen entre si.
Proporción geométrica
Es la igualdad de dos razones geométricas. Se representa como a/b = c/d lo que se lee como: «a es a b como c es a d».
Proporcionalidad directa y proporcionalidad inversa
Cuando comparamos dos segmentos, decimos que son iguales cuando coinciden al superponerlos. En caso de que no coincidan, decimos que son distintos. En este caso, se puede establecer entre ellos una relación de proporcionalidad. La razón de dos figuras iguales entre si es 1.
Magnitudes directamente proporcionales
Son aquellas que aumentan o disminuyen manteniendo siempre la misma relación. Se dice que dos segmentos determinados a y b son directamente proporcionales si al multiplicar uno de ellos por un número cualquiera, también se debe multiplicar el otro por el mismo número para mantener la misma razón. Se suele expresar de la siguiente manera a/b = c/d = k
En este caso, a y b son directamente proporcionales a c y d respectivamente.
Magnitudes inversamente proporcionales
Se dice que dos elementos son inversamente proporcionales cuando al multiplicar uno de ellos por un número, el otro disminuye en la misma proporción. Otra forma de expresarlo es decir que dos magnitudes son inversamente proporcionales cuando su producto permanece constante a pesar de que sus valores varíen. Se suele representar de dos maneras: a·b = c·d = k o bien como a/(1/b) = c/(1/d) = k
En este caso tanto a y b como c y d serían inversamente proporcionales. En el ejemplo de aquí abajo, AB y BC son inversamente proporcionales. Puedes mover el punto A para comprobarlo. Cuanto más aumente el segmento AB, más se reduce el segmento BC, de tal modo que AB·BC siempre es igual a 5.
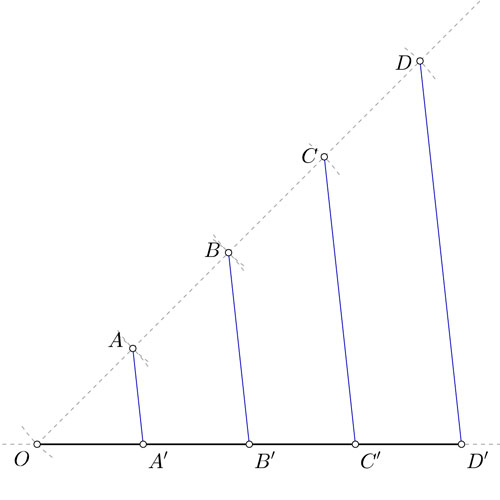
Primer teorema de Tales
Tales de Mileto promulgó dos teoremas que reciben su nombre. Referido a éste apartado, el que a nosotros nos interesa ahora es el primer teorema de Tales, que dice así:
«Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.»
Otra forma de expresarlo sería decir que: «Los segmentos determinados por un haz de rectas paralelas interceptadas por dos rectas oblicuas son directamente proporcionales.»
Siempre teniendo en cuenta que cuando hablamos de triángulos semejantes, estamos hablando de triángulos que tienen todos sus ángulos iguales. Si esto se cumple, sus lados serán proporcionales entre si.
Aplicaciones del Teorema de Tales
Dividir un segmento en partes iguales
Supongamos que tenemos un segmento AB que mide 11cm, y lo queremos dividir en 7 partes iguales. Matemáticamente es un poco difícil, porque 11/7 es igual a 1.571428571428571. Si redondeamos podemos tener problemas, ya que en los últimos segmentos la desviación será mucho mayor.
- Empieza por dibujar el segmento AB, y por uno de sus extremos dibuja una recta auxiliar.
- Sobre esa recta auxiliar, con la ayuda de la regla, mide 7cm y márcalos.
- Une el último de ellos con B, y traza paralelas por el resto.
- Los puntos donde cortan esas paralelas determinan los puntos 1, 2, 3, etc. que determinan siete partes iguales del segmento de 11 centímetros.
Como puedes comprobar, éste sistema te sirve para dividir cualquier segmento en cualquier número de partes. No tiene porque ser siete. Tampoco tiene por que ser en centímetros, puedes usar metros, o cualquier otra medida que se te ocurra.
Hallar la tercera proporcional a tres segmentos
Cuando se habla de hallar la tercera proporcional a tres segmentos lo que se pretende hacer es una regla de tres con esta forma:
A es a B como B es a X
Esto se puede razonar de forma matemática. En el ejemplo que te pongo más abajo, puedes comprobar que B/A da exactamente lo mismo que X/B.
Te voy a explicar dos posibles maneras de hallar la tercera proporcional, ambos válidos. No es necesario que aprendas los dos. Échales un ojo y el que más fácil te resulte, apréndelo.
Para ambos ejemplos vamos a trabajar con dos segmentos de 3 y 2 centímetros respectivamente. De esa manera será una construcción pequeña que podrás realizar en tamaño A4 sin problemas.
Método 1 para hallar la tercera proporcional
- Para éste procedimiento empieza por dibujar una recta auxiliar y sobre esa recta dibuja ambos segmentos, teniendo cuidado de poner primero el más corto.
- Por uno de los extremos dibuja una recta distinta que corte a la primera.
- Sobre esa recta vuelve a dibujar el segmento más largo.
- Une el punto B con D y traza una paralela a esa recta que pase por C. De esa manera obtienes el punto E.
- El segmento que forman D y E es la tercera proporcional.
Aquí abajo puedes mover los puntos B y C para modificar los segmentos AB y BC. Fíjate que la constante k permanece constante y que el segmento DE es proporcional en esa misma cantidad.
Método 2 para hallar la tercera proporcional a tres segmentos
Este método es más rápido, aunque tal vez lo encuentres algo más confuso.
- Empieza por dibujar una recta auxiliar, y sobre ella dibuja el segmento menor.
- Dibujar una recta auxiliar que corte a la primera y sobre ella dibuja el otro segmento.
- Con centro en A y radio hasta C, traza un arco, hallando el punto D.
- Une B con C y luego haz una recta paralela a ésta que pase por D. De esa manera encuentras el punto E.
- El segmento que forman A y E es la tercera proporcional que estás buscando.
Hallar la cuarta proporcional a tres segmentos
El método para hallar la cuarta proporcional a tres segmentos es lo que en matemáticas llamaríamos una regla de tres. La formula matemática vendría a ser algo similar a: A es a B como C es a X (donde X es una incógnita). El método es prácticamente el mismo que el primero que te explicaba más arriba para hallar la tercera proporcional de dos segmentos. Para este ejemplo utiliza tres segmentos de 2, 3 y 4cm. De tal manera que 2 es a 3 como 4 es a X.
- Empieza por dibujar una recta auxiliar, y sobre dicha recta situa el primer segmento AB.
- Dibuja una recta auxiliar que corte a la primera y que pase por A. Sitúa sobre ella el segmento AC.
- Une los extremos de ambos segmentos, es decir, B con C.
- A continuación del primer segmento dibuja el tercer segmento, BD.
- Traza una paralela al segmento que forman B y C, que pase por D. El punto donde corta a la otra recta será E, que determina el segmento CE, cuarta proporcional de los otros tres.
Hallar la media proporcional de dos segmentos.
Hallar la media proporcional de dos segmentos no es hallar la media de dos números. Realmente la formula para verificar esta construcción es un poco más compleja, ya que la media proporcional de dos segmentos es la raíz cuadrada del producto de los dos segmentos que conocemos. Esto significa que la media proporcional de 5 y 9 no será 7. En su lugar será 6,7 centímetros. Puedes verificarlo con la calculadora.
- La forma gráfica para hallarlo es realmente sencilla. En primer lugar, sobre una recta, dibuja ambos segmentos.
- Ahora tienes que hacer la mediatriz para hallar el punto medio de ambos segmentos, al que puedes llamar O.
- Con centro en O y radio hasta A ó C dibuja media circunferencia.
- Levanta una perpendicular al segmento AC que pase por el punto B. El punto donde esa perpendicular corta a la media circunferencia que dibujaste antes tienes el punto D.
- El segmento BD es la media proporcional de los segmentos AB y BC.
Teorema de Pitágoras
Me parece interesante hablar aquí del teorema de Pitágoras, que dice lo siguiente:
«En todo triángulo rectángulo, el cuadrado de la hipotenusa será siempre igual a la suma de los cuadrados de los catetos«
Para que lo entiendas un poco mejor, aquí abajo tienes una aplicación interactiva que lo explica. Puedes mover los vértices B y C del triángulo y verás que siempre se cumple este teorema.
