Problemas de circunferencias tangentes para primero de bachillerato

En ésta sección encontrarás los problemas de circunferencias tangentes más comunes que se suelen encontrar referidos al nivel de primero de bachillerato. Si es la primera vez que te enfrentas a este tipo de ejercicios, es conveniente que primero visites la sección de las rectas tangentes, porque las necesitarás para solucionar algunos de los problemas que encontrarás aquí.

Circunferencias tangentes a una recta por un punto

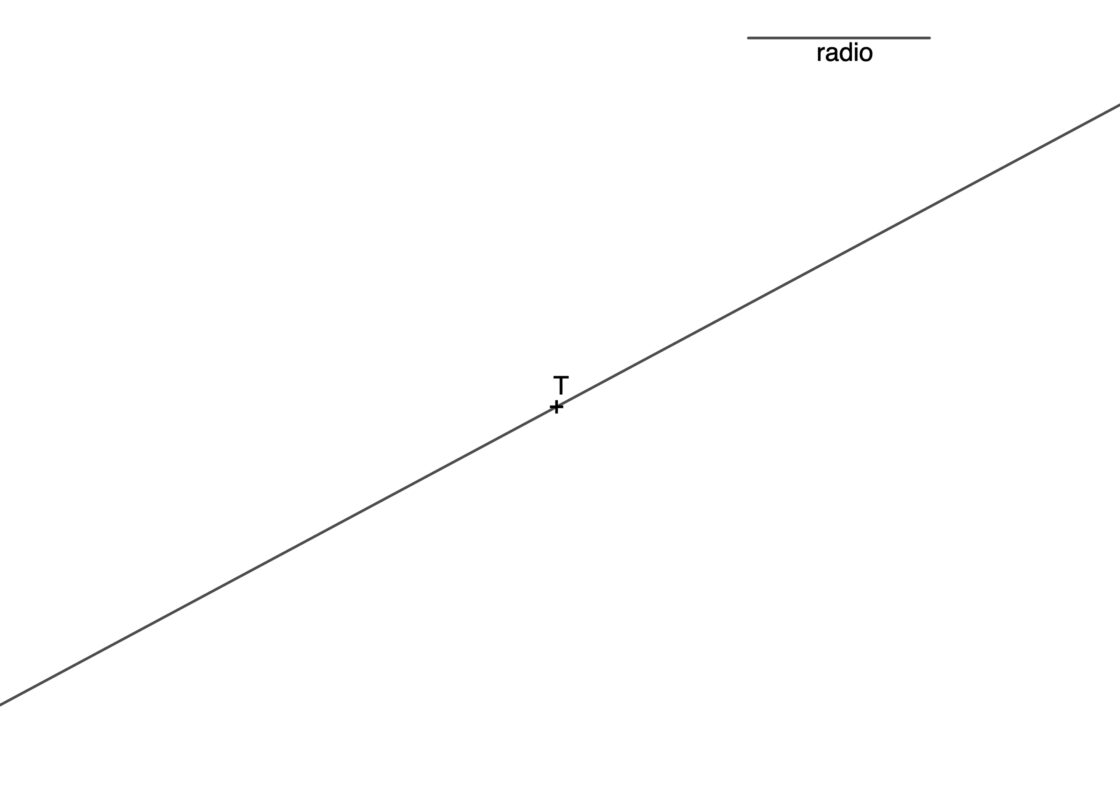
Cuando te enfrentes a este tipo de problemas de circunferencias tangentes te darán una recta conocida, el punto de tangencia T sobre dicha recta, y el radio r de las circunferencias tangentes. Tu punto de partida se parece a esto:

Lo primero que tienes que hacer es dibujar una recta perpendicular a la recta que conocemos que pase por el punto T
Después tienes que medir con el compás la longitud del radio r, y con centro en T, debes trazar dos arcos que cortarán a la recta perpendicular en los puntos O₁ y O₂, que son los centros de las circunferencias que estamos buscando.
Para terminar, con centro en O₁ y radio hasta T, puedes dibujar la primera circunferencia. Con centro en O₂ y radio hasta T, podrás dibujar la segunda circunferencia que se nos pide, y de ese modo resolver el problema.

Aquí abajo tienes un vídeo para que veas como se realiza este ejercicio.

Problemas de circunferencias tangentes a una recta por un punto exterior

Lo primero que te tienen que proporcionar para resolver problemas de circunferencias tangentes de éste tipo es el radio de las circunferencias. Lo más habitual es que te digan cuando mide, de lo contrario no puedes seguir. También conocemos la recta s a la que deben ser tangentes las circunferencias y un punto P por el que pasan y que no pertenece a la recta. Tu punto de partida se parece a esto:

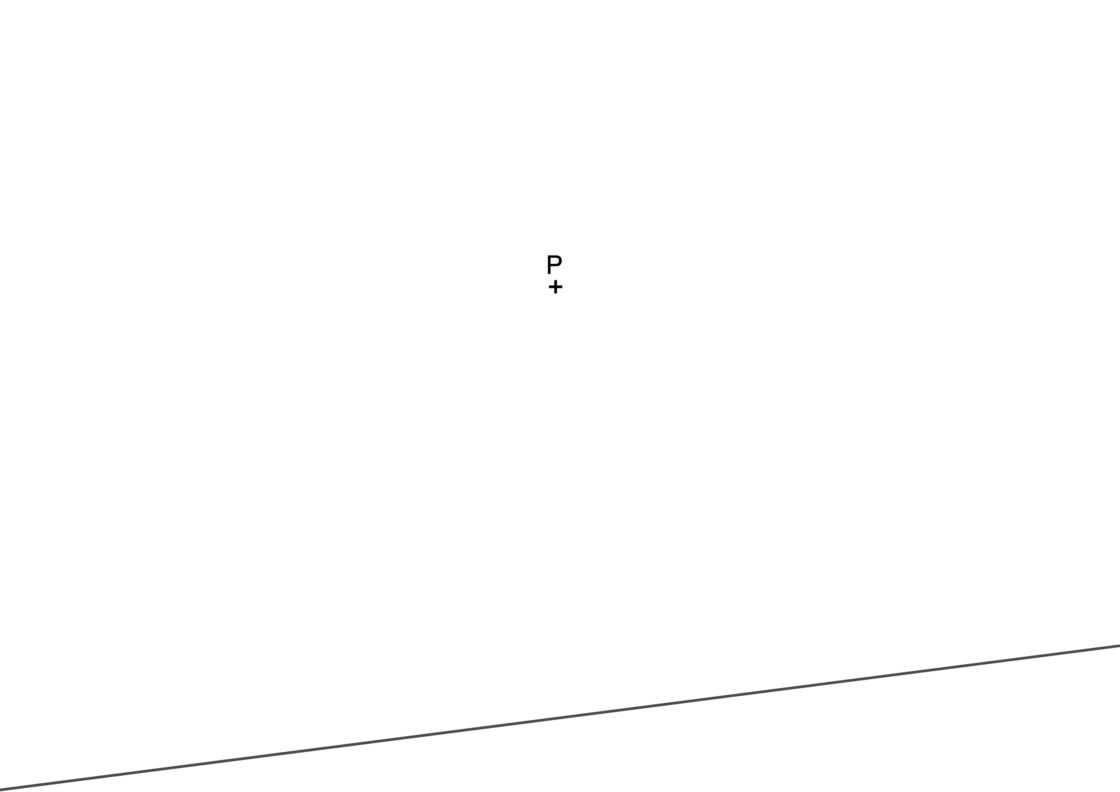
Si imprimes la lámina a tamaño DIN A4 traza circunferencias de radio 6cm, y si las haces en A6 (cuartilla) dibújalas de radio 3cm.

Vas a empezar dibujando una recta paralela a la recta conocida, a una distancia de la misma igual al radio de las circunferencias que te piden.
El siguiente paso es medir con el compás el radio r de las circunferencias. Con ese mismo radio, y centro en T, tienes que trazar un arco que cortará a la recta paralela en los puntos O₁ y O₂ que son los centros de las circunferencias que estás buscando.
Para terminar, con centro en O₁ y radio hasta T, puedes dibujar una de las circunferencias. Luego con centro en O₂ y radio hasta T podrás trazar la otra y de esa manera acabar de solucionar el ejercicio.

Y si por si acaso todavía no acabas de entender como se resuelve este ejercicio, aquí abajo te dejo un vídeo donde puedes ver el proceso completo.

Circunferencias tangentes a una recta y una circunferencia conociendo el punto de tangencia en la circunferencia

En ésta ocasión se te pide hallar las circunferencias tangentes a una recta dada r, y a una circunferencia de centro O₁, cuando conoces también el punto de tangencia sobre esa circunferencia, al que llamaremos T. Para resolverlo es interesante acordarse de las propiedades de las tangencias. Por ejemplo, como ya sabes, los centros de dos circunferencias tangentes se encuentran alineados entre si y con el punto de tangencia. Tu punto de partida se parecerá a este:

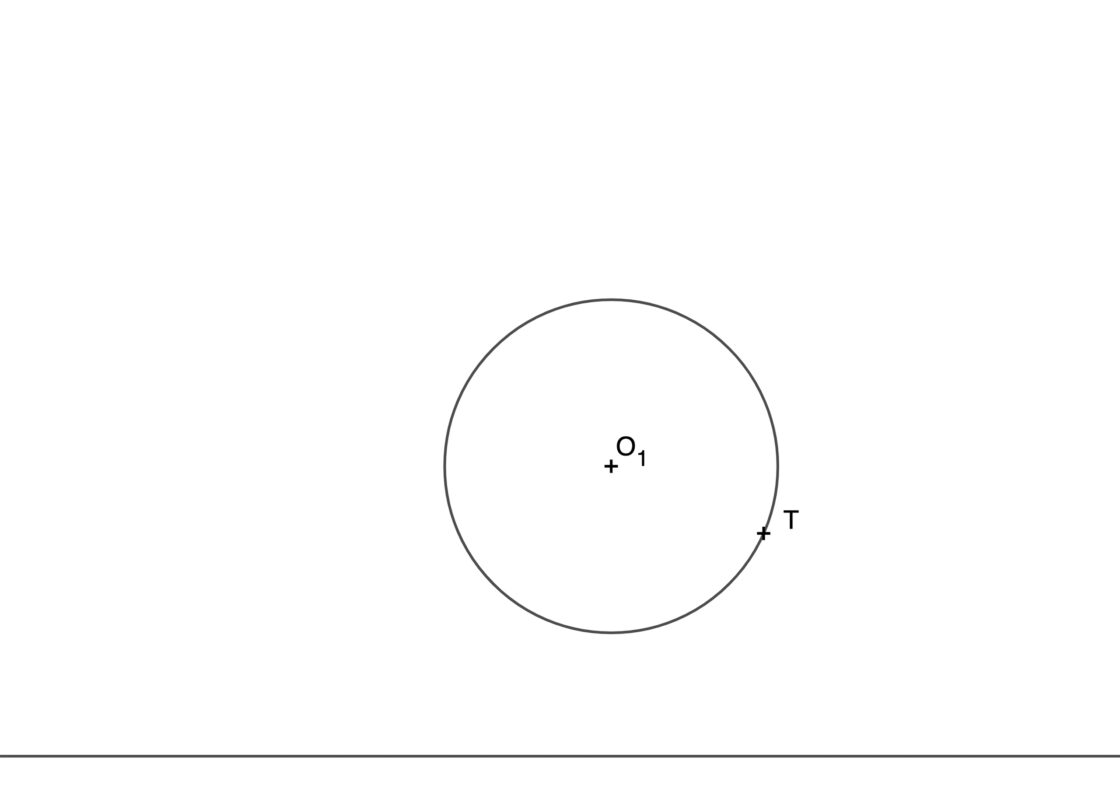
Así pues, lo primero que debes hacer es dibujar la recta que pasa por O₁ y por T.
Ahora traza una perpendicular a dicha recta que pase por T. El punto donde corta a la recta r lo llamaremos P.
Llegados a éste punto hay dos formas de solucionarlo…
- Con centro en P y radio hasta T, traza un arco de circunferencia. De esa manera obtienes T₂ y T₃. Dibujando perpendiculares por esos puntos tienes en la intersección con la recta que pasa por O₁ y T los puntos O₂ y O₃, centros de las circunferencias buscadas.
- Otra posible solución es dibujar las bisectrices que forman la recta que pasa por T y P y la recta r. En la intersección de esas bisectrices con la recta que pasa por O₁ y T tienes los puntos O₂ y O₃, centros de las soluciones buscadas.

Aquí abajo tienes un vídeo donde puedes ver todo el proceso, por si acaso se te planteara alguna duda.

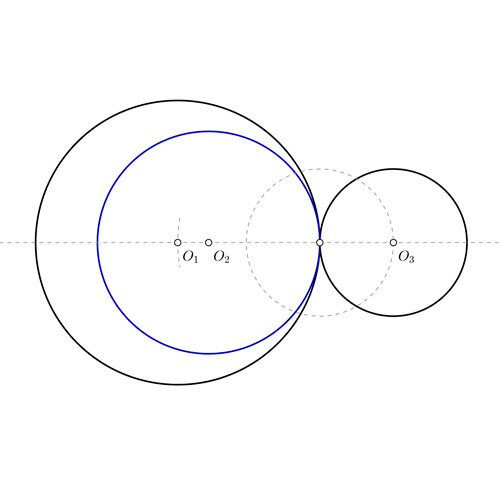
Circunferencia tangente a dos circunferencias conociendo los puntos de tangencia

Este problema es muy sencillo de resolver. Para ello solo debemos acordarnos de las propiedades de las tangencias. Partimos de la base de dos circunferencias de centros O₁ y O₂, también conocemos los puntos de tangencia con la circunferencia que se pide resolver, T₁ y T₂.

Todo lo que debemos hacer es recordar que si dos circunferencias son tangentes entre si, entonces los centros de las mismas están alineados entre si, y con los puntos de tangencia. Para empezar, vamos a dibujar el primer caso, en el que la circunferencia resultante contiene a las dos iniciales. Tu punto de partida se parece a esto:

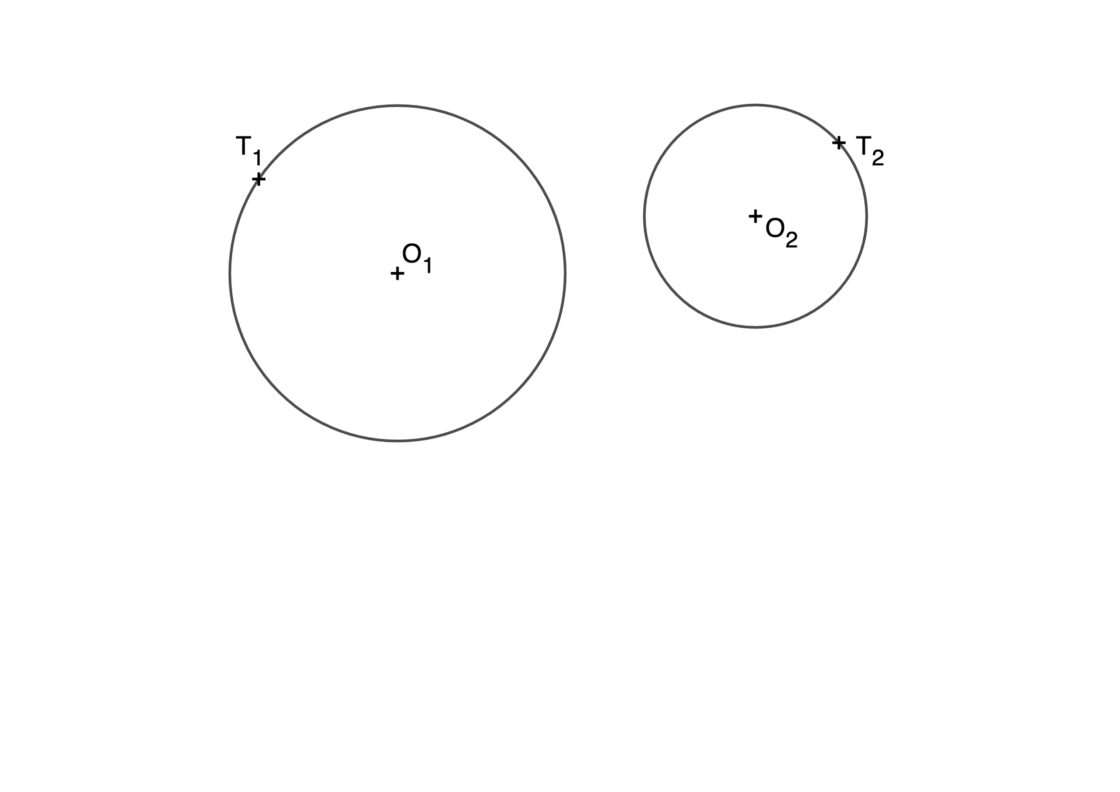
Dibuja las rectas que pasan por T1 y O1 y por O2 y T2. El punto donde se cortan llámalo O3.
Con centro en O3 y radio hasta T1 ó T2, traza una circunferencia. Esa será la solución buscada.

Este ejercicio se puede presentar de distintas formas, dependiendo de dónde se encuentren los puntos de tangencia. De todas formas, no te agobies, porque todas las distintas variedades las puedes resolver de la misma manera. Así, podrías tener las dos circunferencias iniciales dentro del resultado, solo una de ellas, o ninguna de ellas. Aquí tienes un par de ejemplos para que puedas practicar. Este primero contendrá a una de las dos circunferencias iniciales. Tu punto de partida será este:

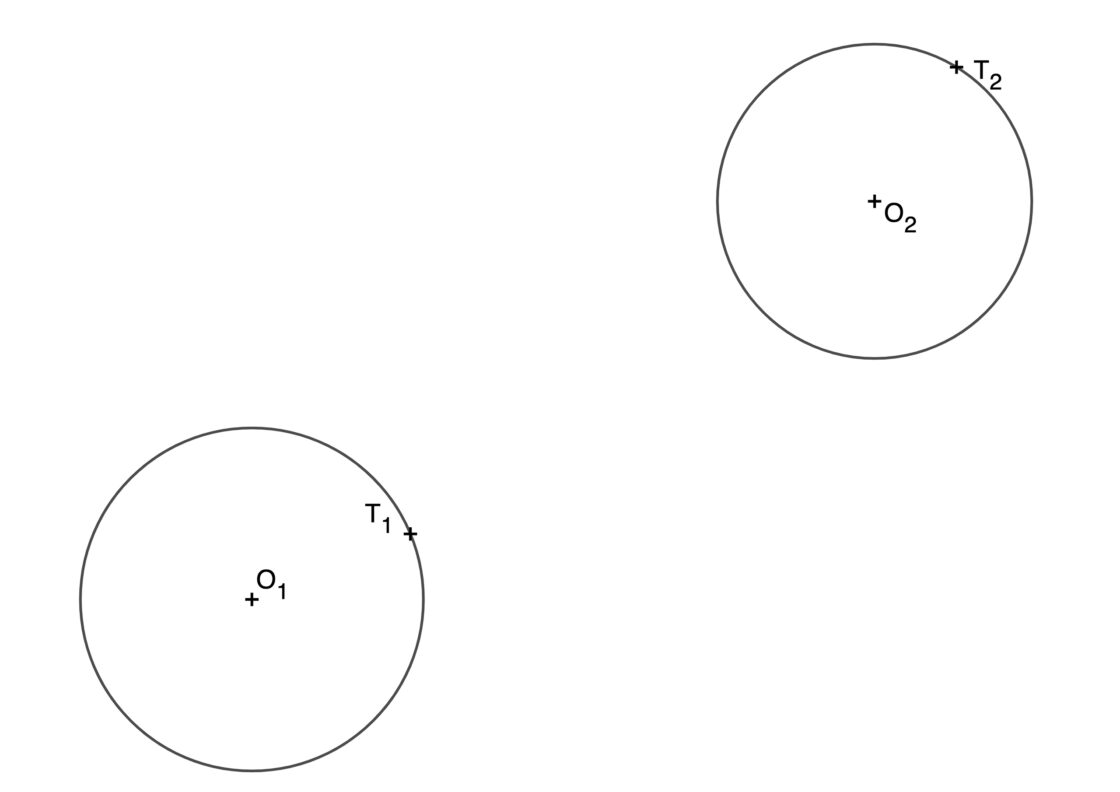
Y en este segundo ejemplo el resultado no contiene a ninguna de las dos iniciales. Tu punto de partida será el siguiente:

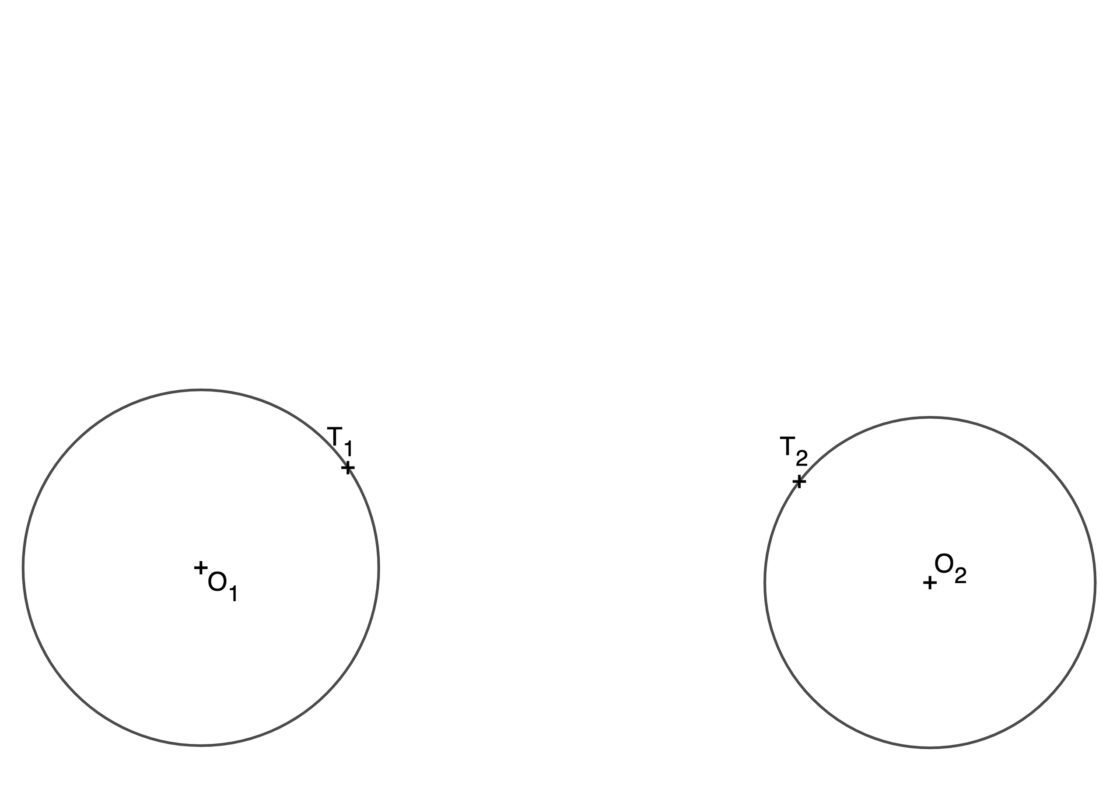
Y aquí tienes una aplicación interactiva en la que puedes mover los centros y los tamaños de las circunferencias para ver cómo se comporta el resultado en cada caso.

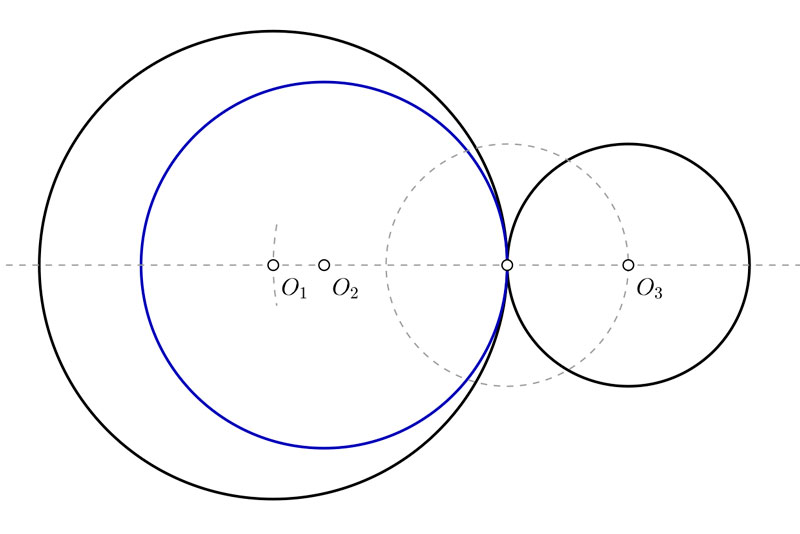
Variante complicada: Conociendo solo uno de los dos puntos de tangencia

Este ejercicio tiene una variante un poco más compleja. Se suele presentar cuando te proporcionan las dos circunferencias, pero solo uno de los dos puntos de tangencia. En este caso tendrás dos soluciones posibles. Una pequeña que no contendrá ninguna circunferencia, y una grande que contendrá a ambas. El punto de partida es similar al de la siguiente imagen. Puedes pulsar sobre ella para que se abra a pantalla completa e imprimirla en un DIN A4 para practicar. Tu punto de partida, pues, será el siguiente:

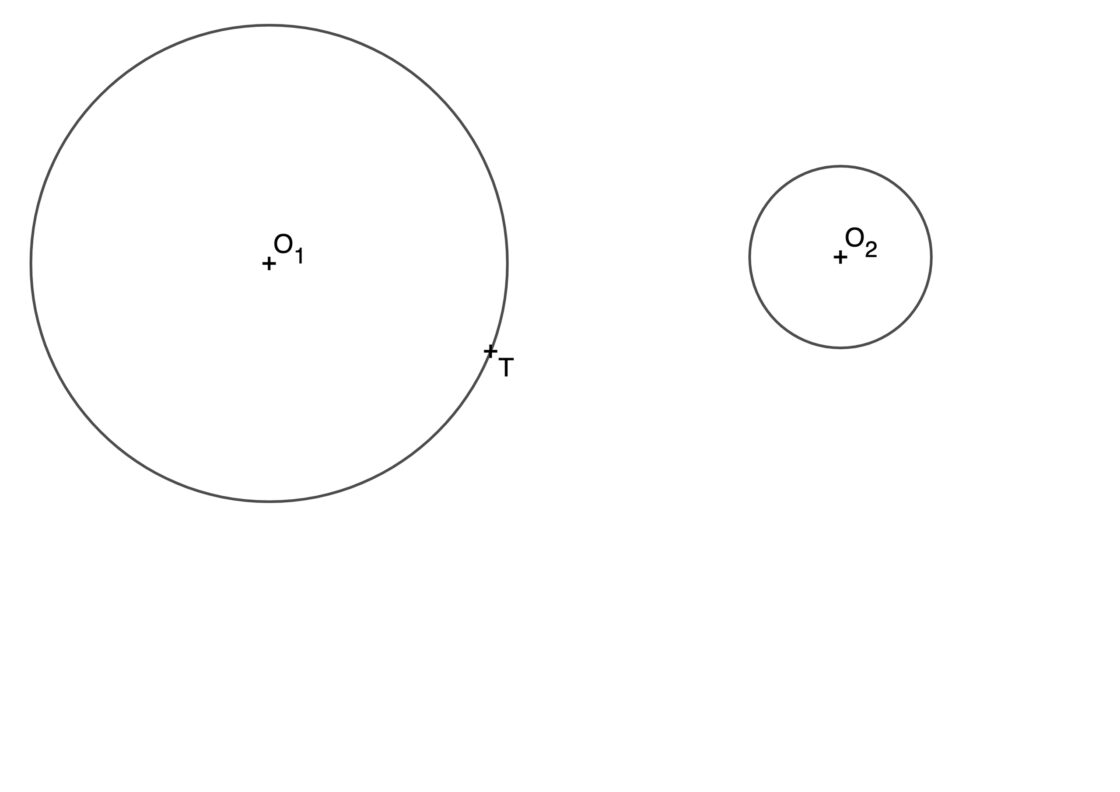
Este problema se resuelve aplicando el principio de las dilataciones. Ese principio es el mismo que se usa para hallar las rectas tangentes a dos circunferencias. Te lo explico con un poco más de detalle:

Dibuja una semirrecta que parte de O₁ y pasa por T. Los centros de las circunferencias solución que buscas estarán sobre esa recta.
Mide el radio de la otra circunferencia, y sobre la recta que acabas de dibujar lleva la distancia de ese radio para sumarla y restarla del radio de O₁. De esa manera obtienes los puntos A y B.
Traza las mediatrices de O₂ con A por un lado, y de O₂ con B por el otro. Los puntos donde esas mediatrices cortan a la recta que pasa por O₁ y T son los centros O₃ y O₄. Estos son los centros de las soluciones que buscas.
Con centro en O₃ y radio hasta T traza una circunferencia. Para terminar, con centro en O₄ y radio hasta T dibuja la otra.

Circunferencias tangentes a dos circunferencias cuando una está dentro de la otra

Este problema es una variante del ejercicio anterior. Se resuelve exactamente igual, la única diferencia es la disposición y el tamaño de las circunferencias. Date cuenta de que los elementos que conoces al empezar son los mismos. Dos circunferencias y el punto de tangencia sobre una de ellas. Puedes tener dos ejercicios distintos, dependiendo de si el punto de tangencia está sobre la mayor o sobre la menor. No obstante, se resuelven igual.

Cuando el punto de tangencia está sobre la menor

Tu punto de partida será similar a esto que ves a continuación:

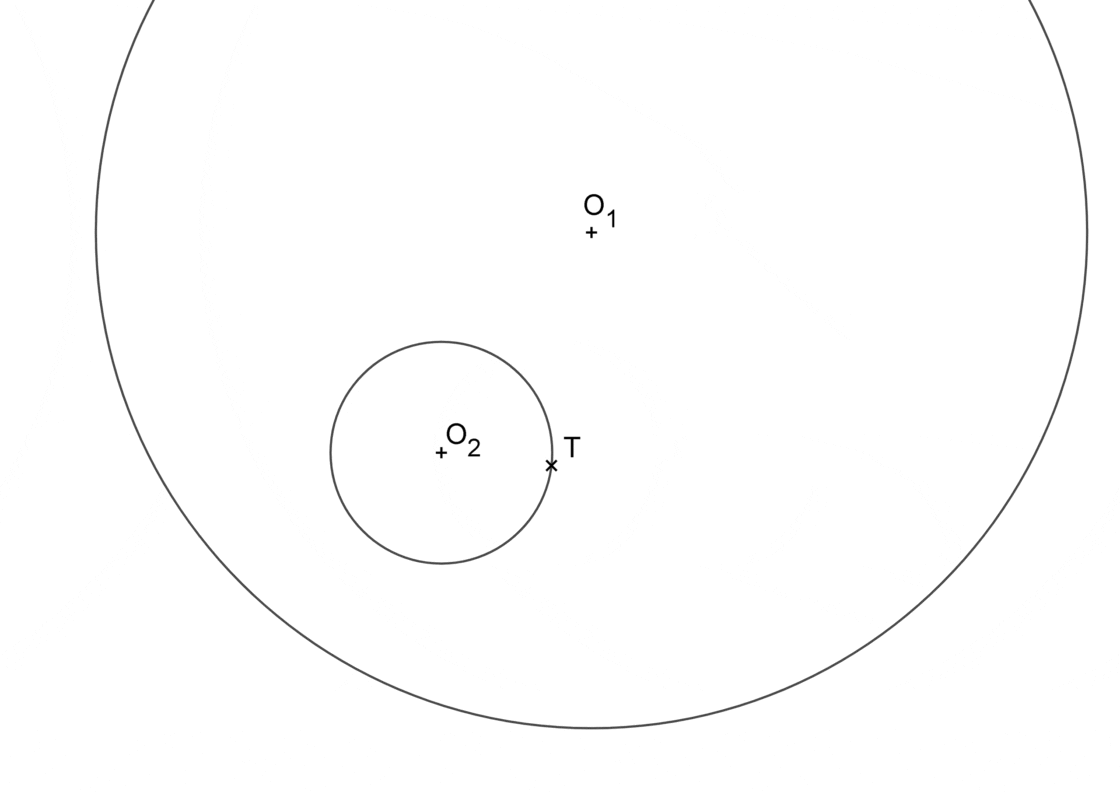
Fíjate que se resuelve repitiendo los pasos del ejercicio anterior, ya que aunque no te lo parezca, es lo mismo.

Traza la recta que une T con O₂ y prolóngala en ambas direcciones, la llamaremos r para referirnos a ella.
Sobre esa recta, lleva el radio de la otra circunferencia, obteniendo A y B.
Donde las mediatrices de O₁A y O₁B cortan a r tienes O₃ y O₄
Con centro en O₃ y O₄ y radio hasta T, puedes dibujar las circunferencias solución.

Cuando el punto de tangencia está sobre la circunferencia mayor

Aunque parezca distinto, sigue siendo una vez más el mismo ejercicio. Tu punto de partida es parecido a esto:

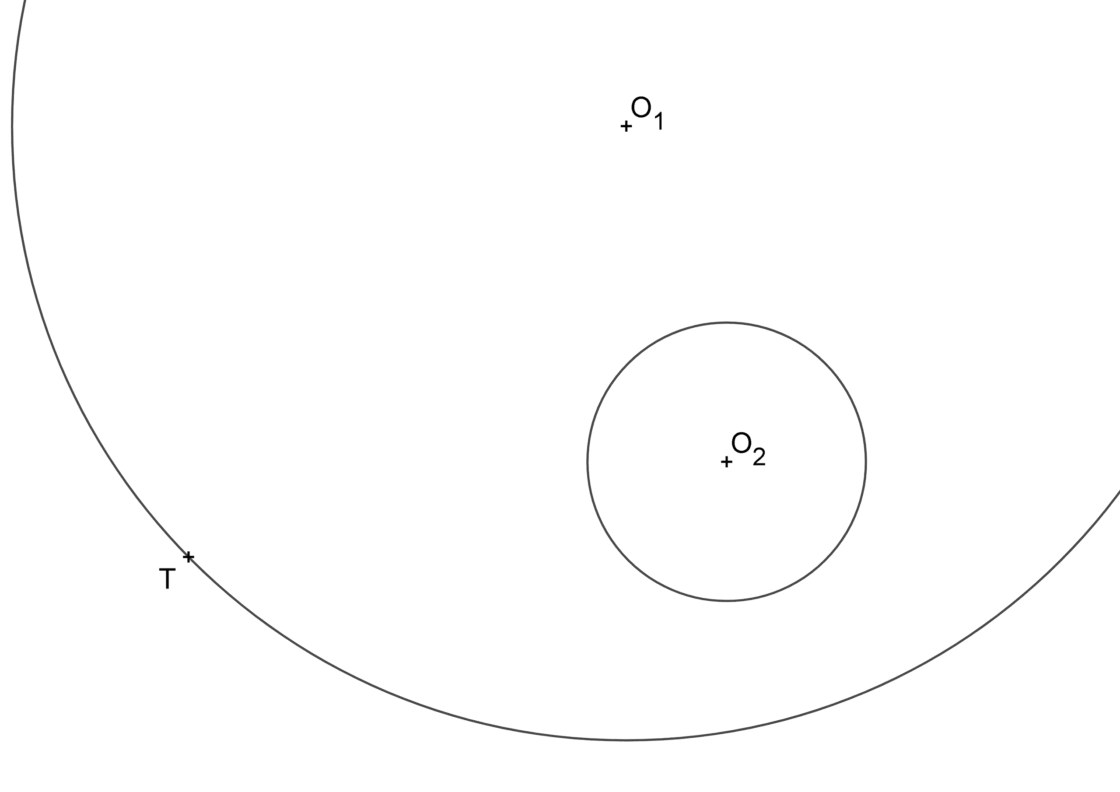
Dibuja la línea que une T con el centro de su circunferencia (en este caso es O₁) y prolóngalo en ambas direcciones.
Sobre esa recta, mide el radio de la circunferencia menor, hallando los puntos A y B.
Ahora haz las mediatrices de O₂A y de O₂B y mira donde cortan a la recta anterior. Esos puntos de corte son O₃ y O₄
Con centro en O₃ y O₄ y radio hasta T puedes dibujar las dos circunferencias solución.

Circunferencias tangentes a una recta y una circunferencia conociendo el punto de tangencia sobre la recta

Este procedimiento es similar al anterior. La diferencia es que cambiamos una de las circunferencias por una recta. Pero si te imaginas que una recta es una circunferencia con el centro en el infinito, el procedimiento es exactamente el mismo. El punto de partida será algo parecido a esto:

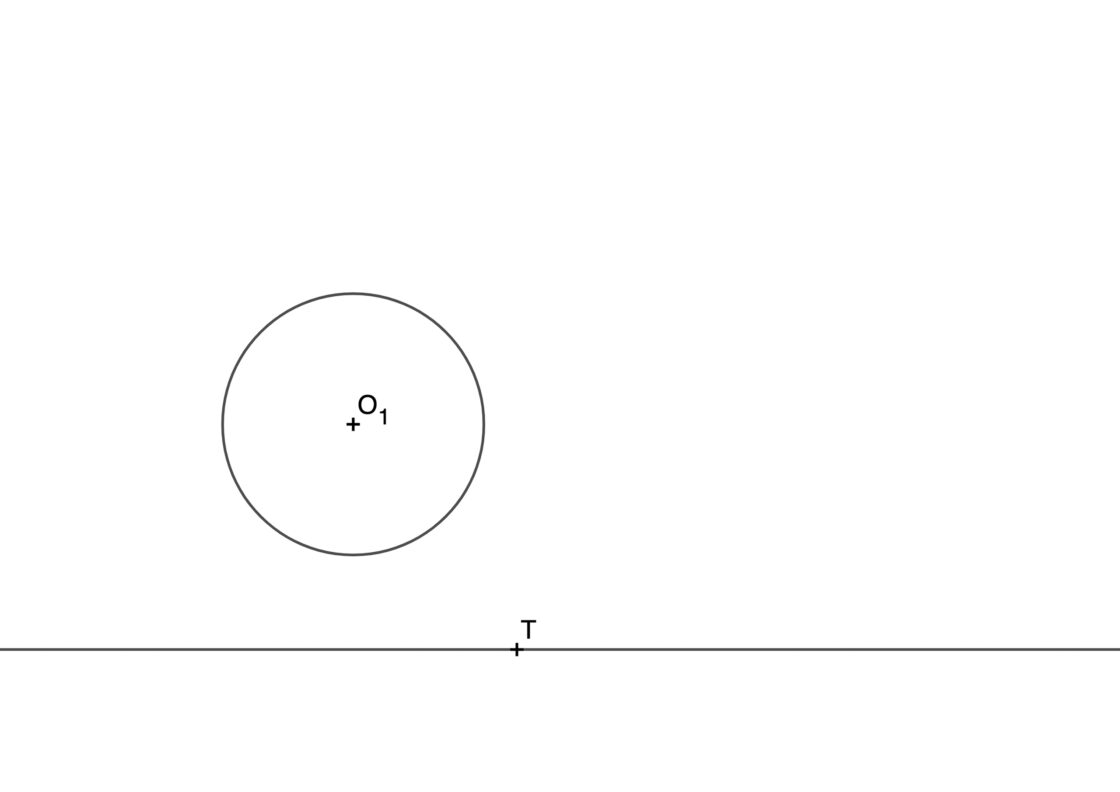
Dibuja una perpendicular por el punto de tangencia T que conoces, ya que sobre el estarán los centros de las soluciones que buscas.
Sobre esa perpendicular, tanto hacia un lado, como hacia el otro, lleva la medida del radio de la circunferencia de centro O₁. De esa manera obtienes los puntos A y B.
Realiza las mediatrices de O₁A y de O₁B. Donde esas mediatrices cortan a la perpendicular que pasa por T tienes los centros O₂ y O₃ de las circunferencias que buscas.
Con centro en O₂ y O₃, y radio hasta T, puedes dibujar las circunferencias de la solución.

¿Y si te digo que este ejercicio es exactamente el mismo que el anterior? ¿No te lo crees? Haz zoom para reducir mucho lo que ves. Te darás cuenta de que lo que tu creías una recta, en realidad es otra circunferencia mucho más grande que contiene a la menor.

Tres circunferencias tangentes entre si conocidos los centros

Los elementos que conocemos para poder resolver éste tipo de ejercicios son los centros de tres circunferencias, representados por los vértices de un triángulo. Para resolver este problema debemos recordar las propiedades de los triángulos. Concretamente del incentro. Si no lo recuerdas, el incentro es el centro de la circunferencia interior al triángulo y tangente a los lados del mismo. Por las propiedades de las tangencias sabemos que los radios que van desde el incentro a los puntos de tangencia serán perpendiculares. Del mismo modo, sabemos que si dibujamos rectas tangentes a un par de circunferencias que son tangentes entre si, también son perpendiculares al segmento que une los centros. Así pues, tu punto de partida se parecerá a esto:

Dibuja las bisectrices de dos ángulos cualquiera del triángulo que conoces. En la intersección de esas bisectrices tendrás O₄, el incentro del triángulo.
Traza perpendiculares a cada uno de los lados y que pasen por O₄. Donde esas perpendiculares cortan a los lados tienes T₁, T₂ y T₃, puntos de tangencia de las circunferencias.
Con centro en O₁ y radio hasta T₁ dibuja la primera de las tres circunferencias.
Ahora dibuja la circunferencia de centro O₂ y radio hasta T₂.
Para finalizar, traza una circunferencia con centro en O₃ y radio hasta T₃.

Aquí abajo tienes un vídeo explicando todo el proceso, por si tienes alguna duda al respecto.