El problema de Apolonio hace referencia a como hallar las circunferencias tangentes a tres circunferencias dadas. Éste problema tiene ocho soluciones posibles, como veremos más adelante. Para poder resolver éste ejercicio es importante conocer diversos recursos didácticos que nos van a ayudar a resolverlo, como son el eje radical de dos circunferencias, el centro radical de tres circunferencias y el de recta polar de una circunferencia respecto a un punto. Para no hacer ésta explicación demasiado farragosa, porque os aseguro que la cantidad de lineas y puntos que vais a ver es realmente sorprendente, iré poniendo imágenes de cada paso, y para los pasos siguientes iré borrando los pasos ya dados para simplificar la visibilidad de los pasos siguientes.
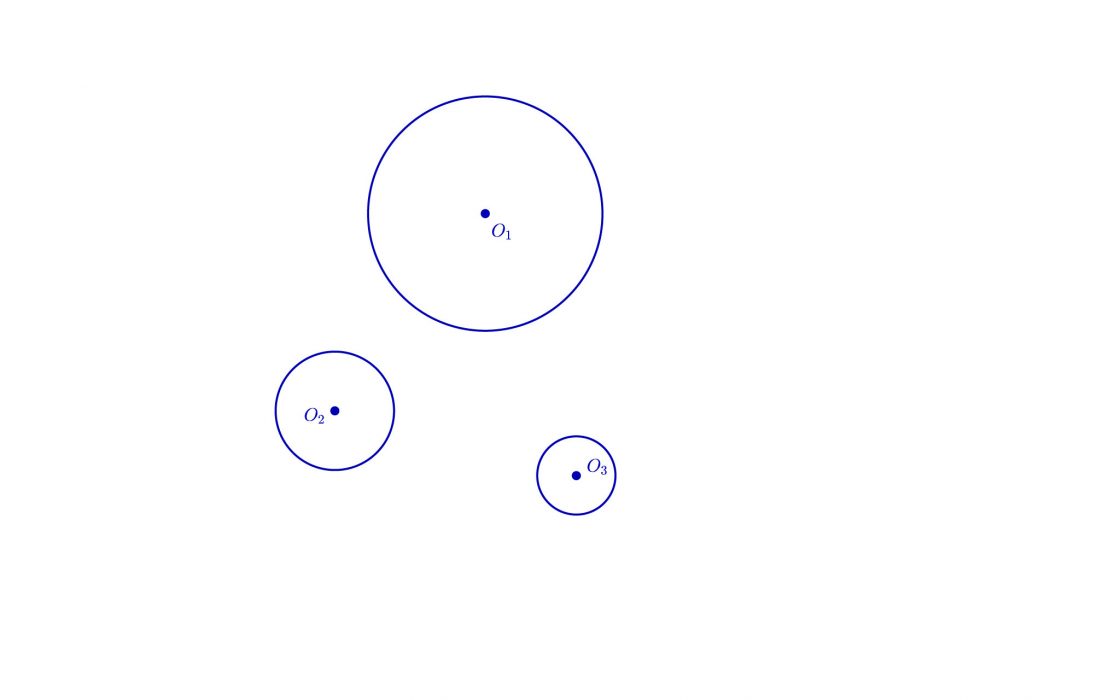
Partimos de tres circunferencias conocidas cuyos centros hemos llamado O1, O2 y O3.
Paso 1: Hallar los seis centros de homotecia
En primer lugar, hallaremos todos los centros de homotecia (seis en total).
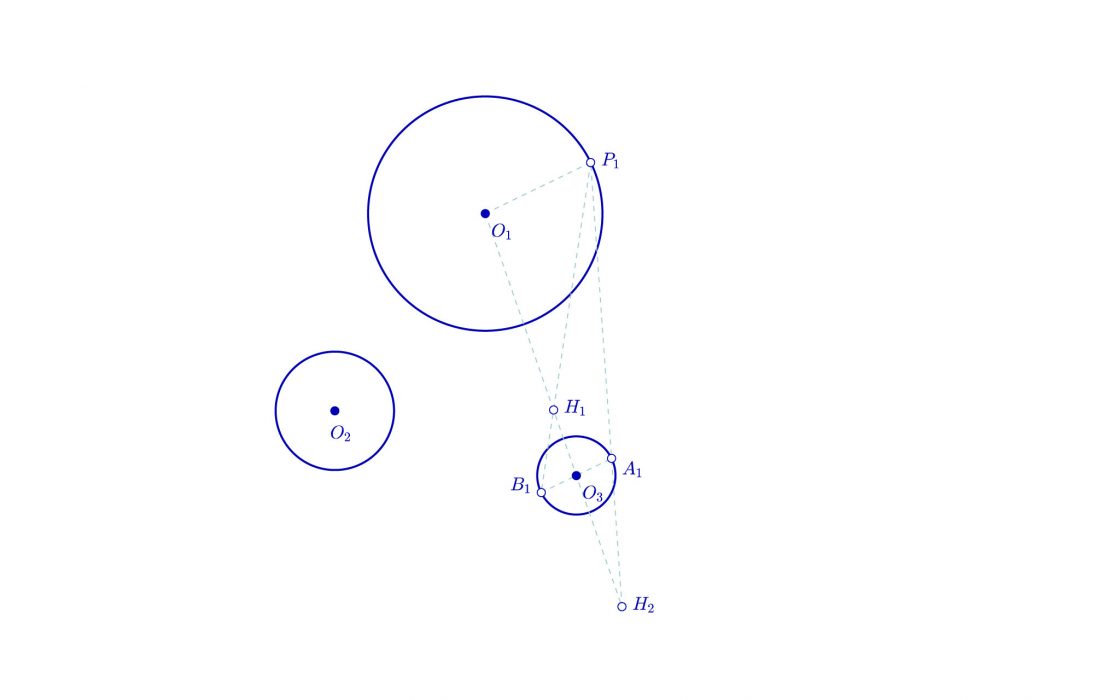
Hallamos los puntos de homotecia de O1 y O3
- Trazamos una recta que une O1 con O3.
- Ahora trazaremos un segmento que parte de O1 y que corta a la circunferencia en cualquier punto P1
- Trazamos una recta paralela al segmento O1P1 que pasa por el centro de O3.
- Obtenemos los puntos A1 y B1, donde dicha recta paralela corta a la circunferencia de centro O3
- Unimos P1 con A1 y B1, en los puntos donde corta a la recta que pasa por O1 y O3 tenemos los centros de homotecia de O1 y O3, a los que vamos a llamar H1 y H2.
Hallamos los puntos de homotecia de O1 y O2
- Trazamos una recta que pasa por O1 y O2.
- Acto seguido realizamos un segmento cualquiera con origen en O1 y que corta en cualquier punto P2 a la circunferencia.
- Trazamos una recta paralela al segmento O1P2 y que pasa por O2. Así obtenemos los puntos A2 y B2 en los puntos de corte de ésta recta con la circunferencia de centro O2.
- Unimos P2 con B2, y en punto en donde corta la recta que une O1 y O2 tenemos el tercer punto de homotecia al que llamaremos H3.
- Unimos P2 con A2 y en su prolongación, al cortar la recta que pasa por O1 y O2 obtenemos el cuarto punto de homotecia que llamaremos H4.
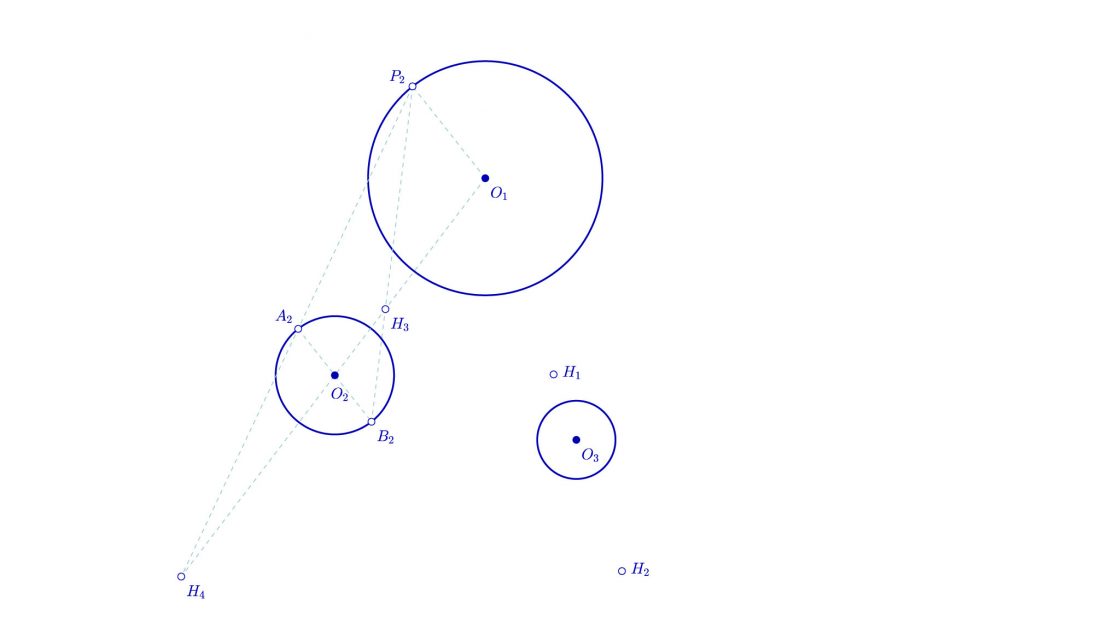
Hallamos los puntos de homotecia de O2 y O3
Como imagino que estáis viendo, resolver el problema de Apolonio no es excesivamente complejo, pero si bastante tedioso. Trabajando sobre el papel debemos ser muy cuidadosos. Es recomendable ir borrando los pasos intermedios para no confundirnos con la cantidad de lineas que se pueden llegar a generar. El proceso es como en los dos pasos anteriores, no obstante lo repetiré para que quede claro.
- Trazamos una recta que pasa por O3 y O2.
- Ahora vamos a dibujar un segmento cualquiera con origen en O2 y que corta en cualquier punto P3 a la circunferencia.
- Trazamos una recta paralela al segmento O2P3 y que pasa por O3. Así obtenemos los puntos A3 y B3 en los puntos de corte de ésta recta con la circunferencia de centro O3.
- Unimos P3 con B3, y en punto en donde corta la recta que une O3 y O2 tenemos el quinto punto de homotecia al que llamaremos H5.
- Unimos P3 con A3 y en su prolongación, al cortar la recta que pasa por O3 y O2 obtenemos el sexto punto de homotecia que llamaremos H6.
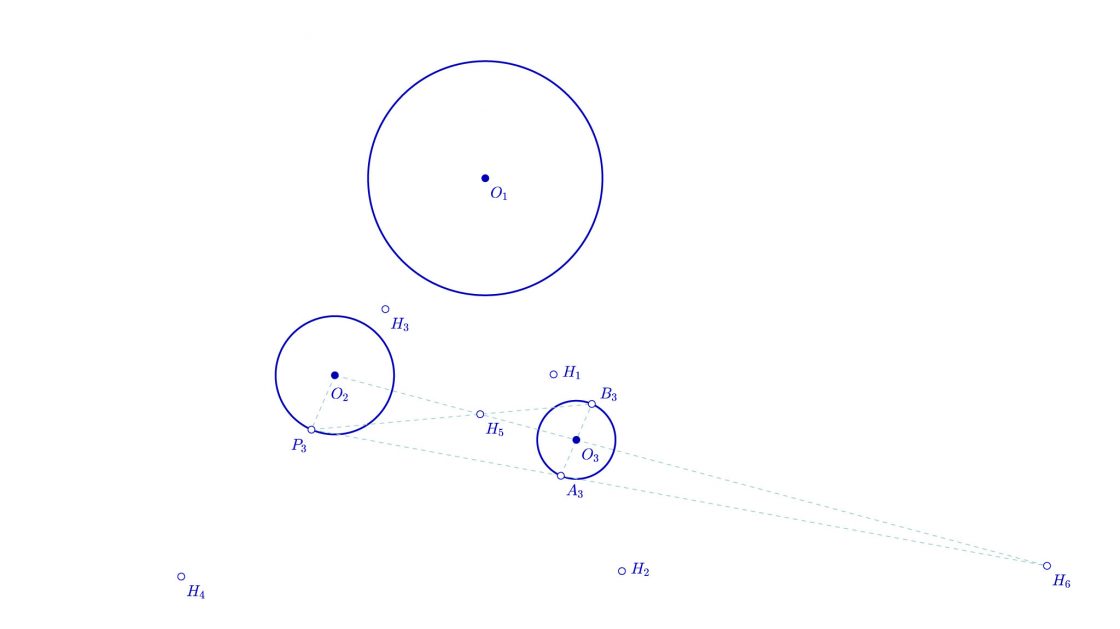
Resolviendo el problema de Apolonio: Hallar polos
Para continuar la resolución del problema de Apolonio, hemos de hallar los polos de cada una de las circunferencias respecto a las rectas polares que forman los centros de homotecia alineados en grupos de tres entre si.
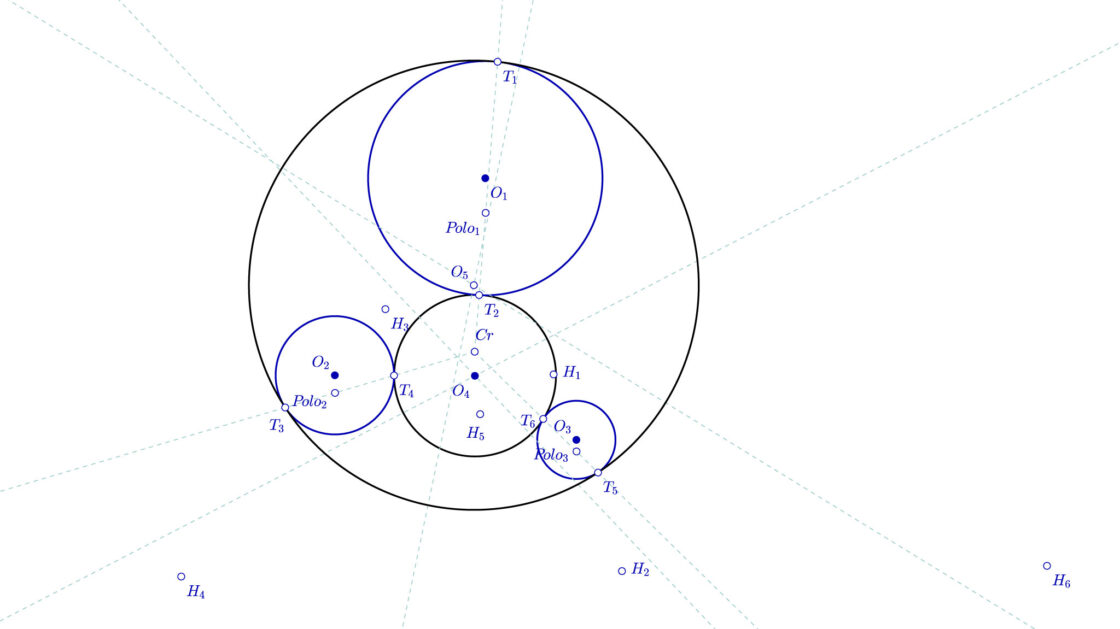
Llegados a éste punto voy a hacer una pequeña aclaración… Si os fijáis, hay cuatro posibles rectas polares. Os pondré una imagen para que lo veáis más claro.
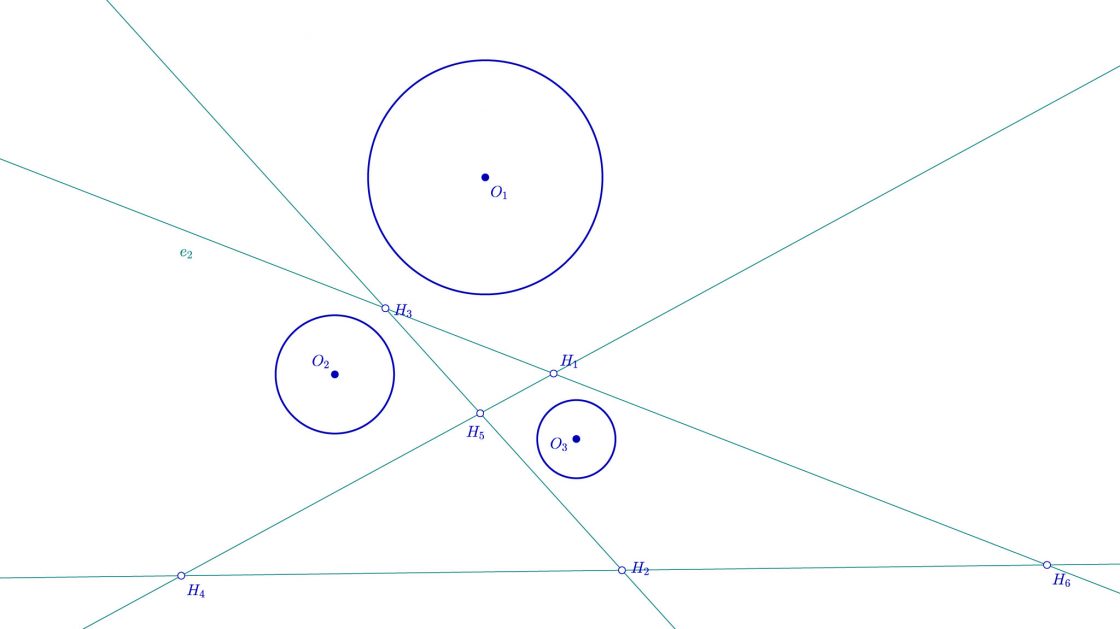
Cada uno de éstos ejes determina dos posibles circunferencias tangentes a éstas tres circunferencias, por eso hay ocho posibles soluciones. Más aún, si os fijáis bien, tres ejes pasan entre las circunferencias, mientras que uno de ellos pasa por fuera. Los ejes que pasan entre las circunferencias Siempre contienen una o dos de las circunferencias. Pero el eje que no pasa entre ellas es el que determina las circunferencias inscrita y exinscrita, es decir, la circunferencia que contiene a las tres circunferencias a la vez y la que no contiene a ninguna de ellas. Vamos a empezar pues con éste eje.
Para ello debemos recordar como hallar tangencias, pues lo vamos a necesitar.
- Empezaremos por la recta que forman H4, H2 y H6. A ésta recta polar la llamaremos e1.
Hallamos el polo de O1 respecto a e1
- Trazamos una perpendicular a e1 y que pasa por O1. El punto en el que corta a e1 lo llamaremos Base1.
- Hallamos uno de los puntos de tangencia de una recta que pase por Base1 con la circunferencia de centro O1. Para ello hacemos lo siguiente:
- Hallamos el punto medio del segmento O1Base1, al que llamaremos C1.
- Con centro en C1 y radio C1O1 trazamos una circunferencia que corta a la circunferencia de centro O1 en un punto al que vamos a llamar Tangencia1.
- Trazamos una paralela a e1 y que pasa por Tangencia1, en el punto en el que corta al segmento O1C1 tenemos el Polo de O1 respecto al eje e1. A éste punto lo llamaremos Polo1.
Hallamos el polo de O2 respecto a e1
- Trazamos una perpendicular a e1 y que pasa por O2. Al punto en que corta a e1 lo vamos a llamar Base2.
- Hallamos uno de los puntos de tangencia de una recta que pasa por Base2 con la circunferencia de centro O2. Para ello procedemos así:
- Hallamos el punto medio del segmento O2Base2, al que llamaremos C2.
- Con centro en C2 y radio C2O2 trazamos un arco de circunferencia que corta a la circunferencia en un punto al que llamaremos Tangencia2.
- Trazamos una paralela a e1 y que pasa por Tangencia2. El punto en el que corta al segmento O2C2 nos determina el segundo Polo, el de O2 respecto al eje e1, al que vamos a llamar Polo2.
Hallamos el polo de O3 respecto a e1
- ¡Vamos a por el último!
- Realizamos una perpendicular al eje e1 y que pasa por O3. Al punto en que corta a e1 lo llamaremos Base3.
- Una vez más, necesitamos localizar uno de los puntos de tangencia de una recta que pasa por Base3 y que sea tangente a la circunferencia de centro O3. Para ello:
- Hallamos el punto medio del segmento que une O3 y Base3, al que llamaremos C3.
- Con centro en C3 y un radio igual al segmento que forman C3 y O3 trazamos un arco que corta a la circunferencia de centro O3 en un punto al que llamaremos Tangencia3.
- Ahora realizamos una recta paralela al eje e1 y que pasa por Tangencia3. El punto en el que corta al segmento C3O3 será el tercero de los polos que buscamos, al que vamos a llamar Polo3.
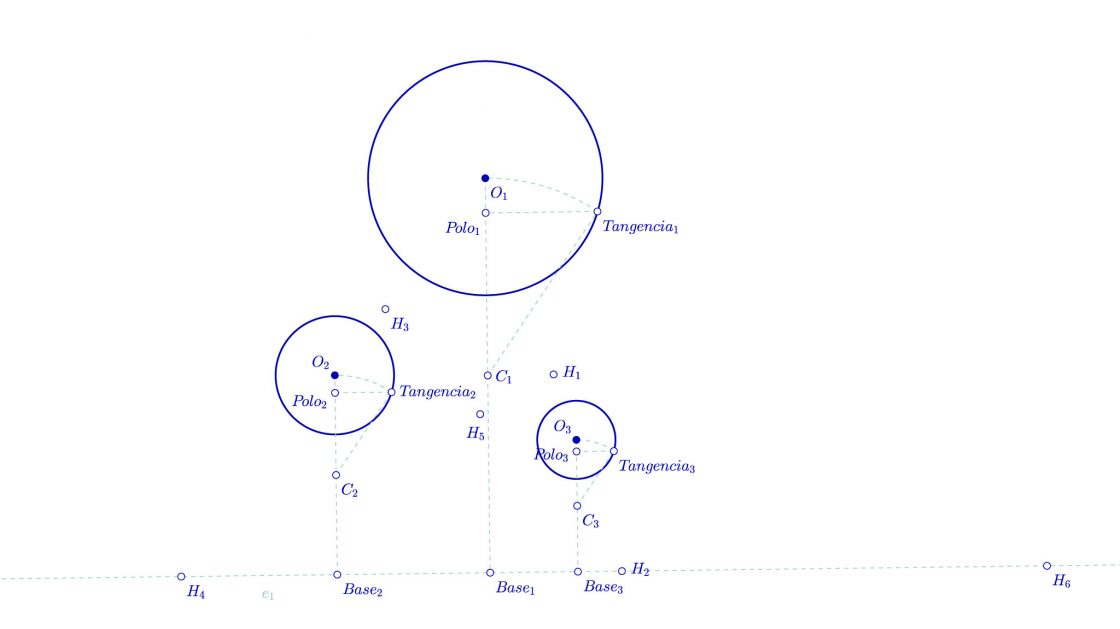
Solucionando el problema de Apolonio: Primer par de circunferencias tangentes
Ya estamos más cerca de solucionar parte del problema de Apolonio y de hallar el primer par de circunferencias tangentes de las ocho posibles que tiene éste problema. ¡Ánimo, que ya falta menos!
Ahora debemos encontrar el centro radical de las tres circunferencias. Para ello procedemos de la siguiente manera:
Hallamos el eje radical de O1 y O2
Primero vamos a hallar el eje radical de las circunferencias de centro O1 y O2. Veamos como:
- Unimos O1 y O2 con un segmento.
- Trazamos la mediatriz de dicho segmento.
- Ahora, con centro en cualquier punto de esa mediatriz, y con cualquier radio, dibujamos una circunferencia auxiliar que corte a las circunferencias de centro O1 y O2. A los puntos de corte los voy a llamar Q1, R1, S1 y X1.
- Unimos Q1 y R1 con una recta, y S1 y X1 con otra recta. El lugar en que se cortan lo llamaremos Y1.
- El eje radical de las circunferencias O1 y O2 es una recta perpendicular al segmento que une los centros de O1 y O2 y que además pasa por Y1, de modo que lo dibujamos y lo llamaremos Eje1.
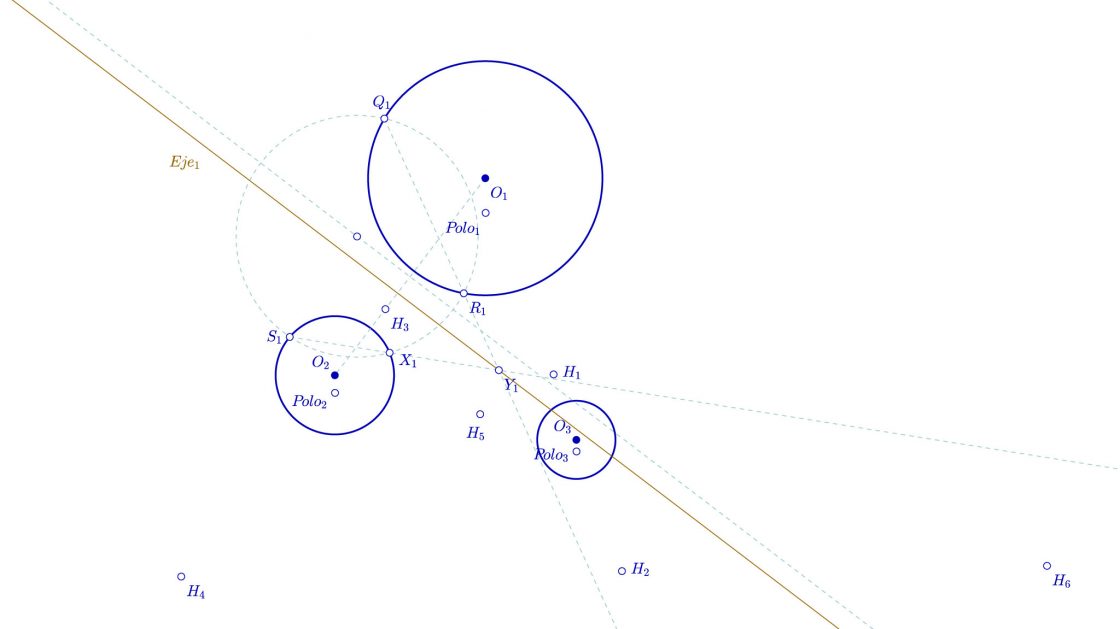
Seguro que a estas alturas ya debéis estar un poco cansados del problema de Apolonio, pero no desesperéis que ya casi lo tenemos…
Hallamos el eje radical de O1 y O3
Para hallar el centro radical de las tres circunferencias necesitaremos otro eje radical, y donde ambos ejes se corten, tendremos el centro radical de las tres circunferencias.
Repetimos los pasos del apartado anterior, pero ésta vez respecto a O1 y O3. Recordemos como:
- Trazamos un segmento que une O1 y O3.
- Hallamos la mediatriz de O1 y O3.
- Sobre dicha mediatriz, con un radio cualquiera que corte a ambas circunferencias, trazamos una circunferencia auxiliar que corta a O1 y O3 en Q2, R2, S2 y X2.
- Trazamos una recta que pasa por R2 y Q2.
- Trazamos una recta que pasa por S2 y X2.
- El punto en que ambas rectas se cortan lo llamaremos Y2. Éste punto se encuentra sobre el eje radical de O1 y O3, por lo tanto lo único que tenemos que hacer es trazar una perpendicular al segmento que une O1 y O3 y que pasa por Y2. Éste será el eje radical buscado, al que llamamos Eje2.
¡Ya lo tenemos! El punto en que el Eje1 y el Eje2 se cortan será el centro radical de las tres circunferencias, al que voy a denominar Cr.
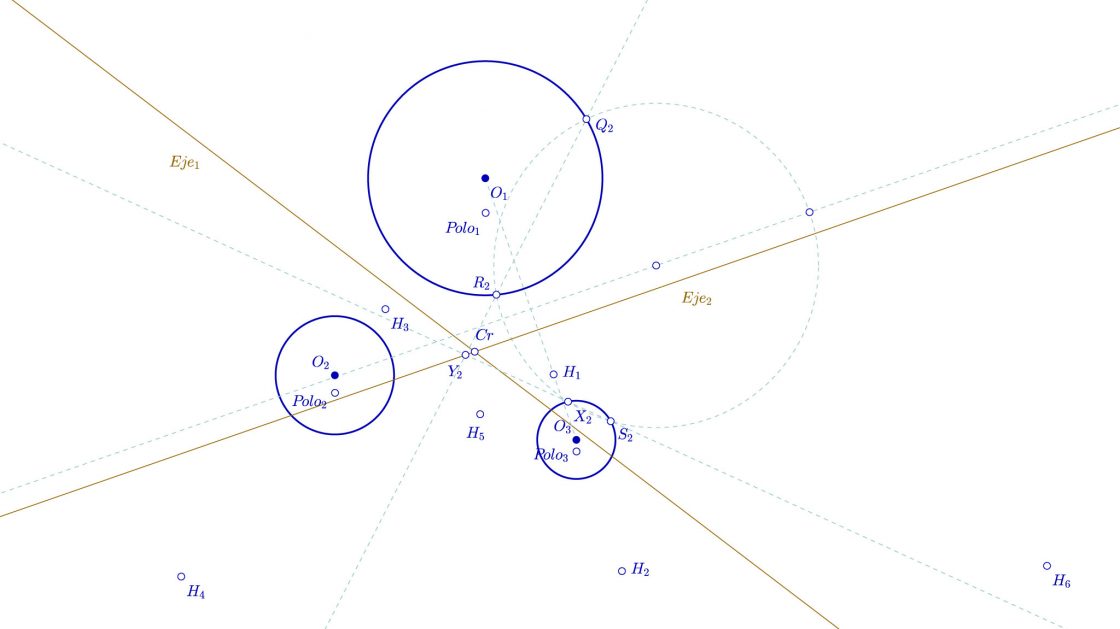
Primera solución al problema de Apolonio
Vamos a hallar el primer par de circunferencias tangentes a éstas tres circunferencias, y de ese modo hallaremos la primera solución posible para el problema de Apolonio, que además suele ser la más solicitada, la de las circunferencias inscritas y exinscritas a éste trío de circunferencias.
Ahora desde el centro radical trazamos rectas que pasan por los polos y cortan a las circunferencias en T1, T2, T3, T4, T5 y T6. Éstos son los puntos de tangencia de las circunferencias interior y exterior.
La primera terna de puntos (T2, T4 y T6) determinan los puntos de tangencia de la circunferencia inscrita. Recordemos que desconocemos el centro de dicha circunferencia.
Hallamos los centros de las circunferencias
Llegados a éste punto, debemos recordar como hallar el circuncentro de un triángulo. Por si lo habéis olvidado, hay que localizar el punto donde las mediatrices del triángulo se cortan. No es necesario hallar las tres mediatrices, con que hallemos dos de ellas nos bastará, de ese modo obtenemos el centro de la circunferencia inscrita a la que vamos a denominar O4.
Con centro en O4 y radio hasta T2, T4 ó T6, trazamos la primera de las ocho posibles circunferencias que son la solución al problema de Apolonio.
Para la segunda procederemos de modo similar… Trazamos las mediatrices de T1 con T3 y de T3 con T5 . En el punto en que se corten tendremos el centro de la circunferencia exinscrita a las tres circunferencias iniciales.
A éste punto lo vamos a llamar O5 . Con centro en O5 y radio hasta T1 , T3 ó T5 , trazamos la circunferencia exinscrita a las tres circunferencias iniciales.

Segunda solución al problema de Apolonio
Vamos a hallar ahora el segundo par de circunferencias tangentes a éstas tres circunferencias. En ésta ocasión vamos a utilizar la terna formada por H3 , H1 y H6 . Estos tres centros de homotecia que teníamos hallados de antes los unimos con una recta a la que vamos a llamar e2 .
Ahora vamos a hallar los polos de las circunferencias respecto a éste eje e2 .
Hallamos el polo de O1 respecto a e2
- Trazamos una perpendicular que pase por el centro de O1 hasta el eje e2, y el punto en el que corta a dicho eje lo llamaremos Base4.
- Hallamos el punto medio del segmento que forman O1 y Base4, al que vamos a llamar C4
- Con centro en C4 y radio igual al segmento que forman O1 y C4 trazamos una circunferencia que corta a la circunferencia de centro O1 en el punto de tangencia al que vamos a llamar Tangencia4
- Realizamos una paralela a e2 que pasa por Tangencia4 y que corta al segmento que forman el centro de la circunferencia de centro O1 y al punto Base4.
- El punto en que se cortan, es el polo de la circunferencia de radio O1 respecto al eje e2. Lo vamos a llamar Polo4.
Hallamos el polo de O2 respecto a e2
- Ahora trazamos una perpendicular al eje e2 que pasa por el centro de la circunferencia con centro en O2. Al punto en que corta al eje e2 lo vamos a llamar Base5.
- Hallamos el punto medio del segmento que forman O2 y Base5, y a dicho punto lo vamos a llamar C5.
- Trazamos un arco con centro en C5 y radio igual al segmento que forman C5 y O2. Este arco corta la circunferencia de centro O2 en un punto de tangencia del punto Base5 respecto a la circunferencia de centro O2. A éste punto lo vamos a llamar Tangencia5.
- Si trazamos una paralela al eje e2 que pasa por Tangencia5, en el punto en que corta al segmento formado por C5 y O2 tenemos el polo de la circunferencia de centro O2 respecto al eje e2. A éste polo lo vamos a llamar Polo5.
Hallamos el polo de O3 respecto a e2
- ¡Vamos a por el último polo de ésta terna!
- Trazamos la perpendicular al eje e2 que pasa por O3, y al punto en que ésta recta corta al eje e2 tenemos un punto al que vamos a llamar Base6.
- Hallamos el punto medio del segmento que une Base6 y O3, y a éste punto medio lo llamaremos C6.
- Trazamos un arco de circunferencia con centro en C6 y radio igual al segmento que forman C6 y O3. Donde corta a la circunferencia de centro O3 tenemos el punto de tangencia de las rectas que pasan por Base6 y son tangentes a la circunferencia de radio O3. A éste punto lo llamaremos Tangencia6.
- Ahora realizamos una recta paralela al eje e2 y que pasa por Tangencia6. En el punto en que corta al segmento que forman C6 y O3 tenemos el polo de la circunferencia de centro O3 respecto al eje e2. A éste punto lo vamos a llamar Polo6.
Hallamos los puntos de tangencia
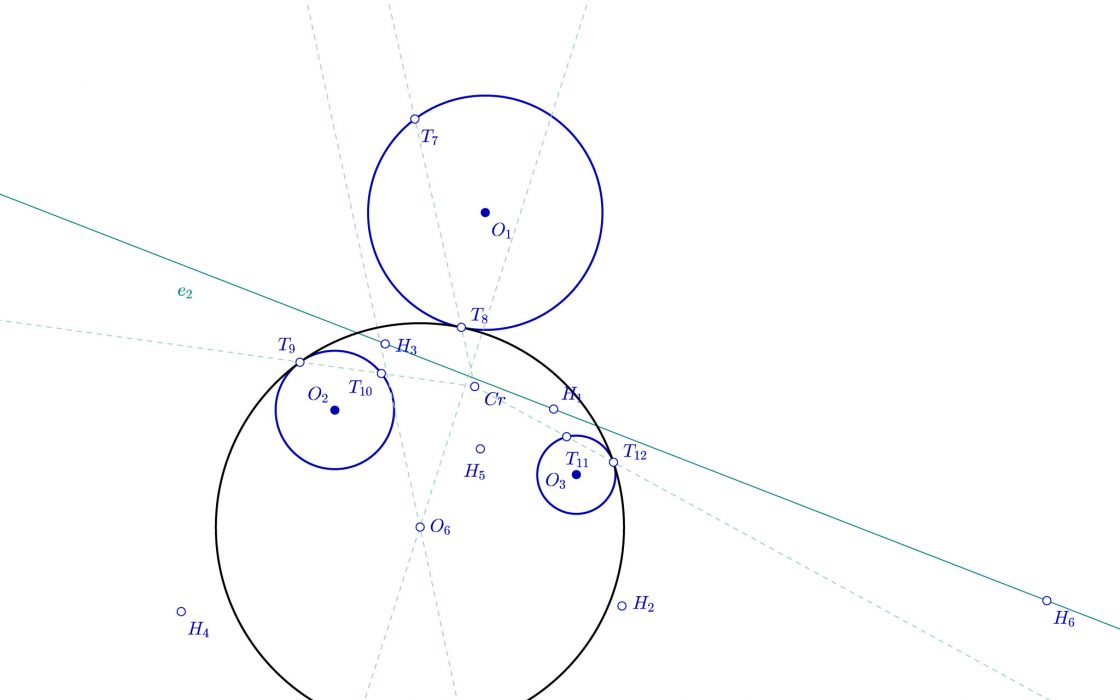
- Llegados a éste punto trazamos rectas que pasan por el centro radical de las tres circunferencias Cr y pasan por Polo4, Polo5 y Polo6. A los puntos en que corta a las circunferencias de centro O1, O2 y O3 los vamos a llamar T7,T8,T9,T10,T11 y T12.
Llegados a éste punto, y para evitar enmarañar todavía más el desarrollo, me voy a permitir el lujo de borrar todos los pasos intermedios de éste apartado y quedarme solo con los puntos T de tangencia y el eje e2 para proceder a la resolución de éste par de circunferencias tangentes.
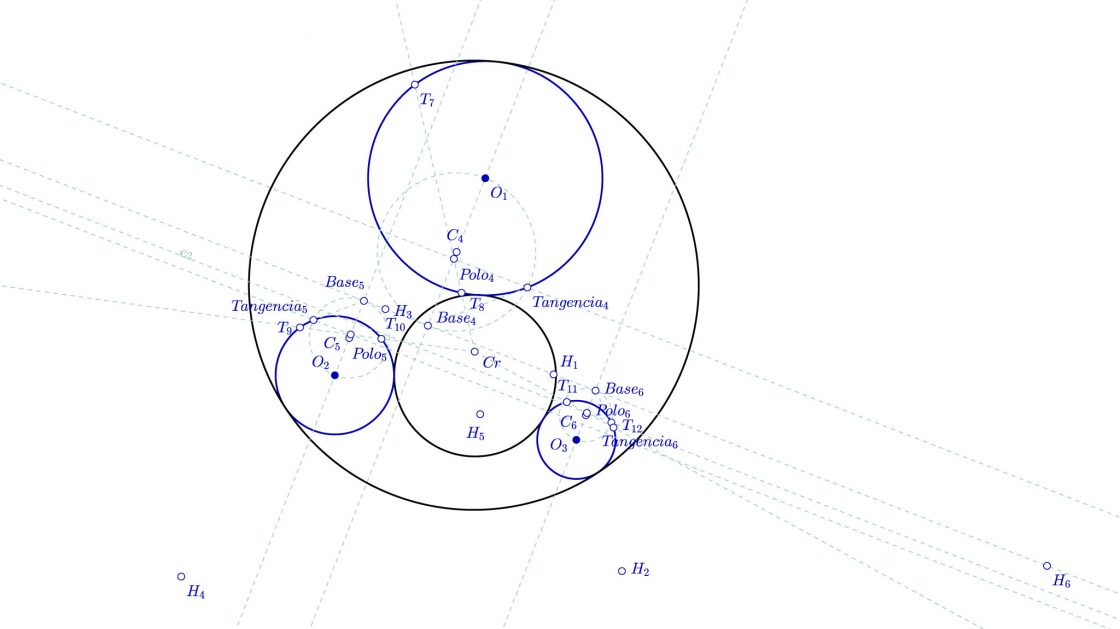
Con lo cual la cosa quedaría así…
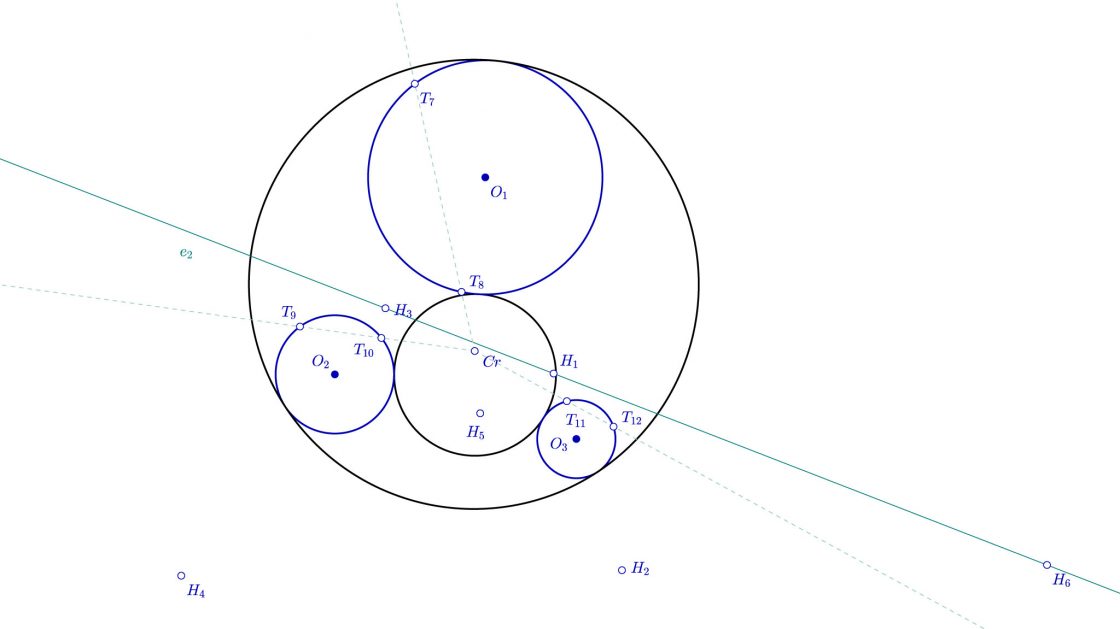
Hallamos los centros de las circunferencias tangentes
¿Cómo sabemos que puntos de tangencia pertenecen a que circunferencias? Podemos hacerlo por intuición o por la técnica de ensayo y error, pero si nos fijamos en el eje es mucho más fácil. El eje deja una circunferencia aislada de las otras dos. Ésta es la que vamos a usar de guía. En una de las circunferencias los tres puntos de tangencia serán el punto de tangencia más cercano al centro radical que pertenece a ésta circunferencia, y por otra parte los puntos más alejados del centro radical de las otras dos. Y por tanto, la otra circunferencia la determinarán los puntos más cercanos al centro radical de las otras dos circunferencias, y el más alejado de la que queda aislada.
Es decir, la primera circunferencia pasa por T8, T9, y T12, y la segunda circunferencia pasará por T7, T10, T11.
Como hallar el centro de la circunferencia conociendo tres puntos
Para hallar el centro de la circunferencia que pasa por T8, T9, y T12, tenemos que hallar donde se cortan las mediatrices de los segmentos que unen estos puntos. Ésta será la tercera circunferencia que será una solución posible al problema de Apolonio. Si no recordáis como se halla el centro, os lo recuerdo rápidamente.
- Con centro en T8 y radio igual al segmento que forman T8 y T9 trazamos un arco.
- Desde T9 y con el mismo radio, trazamos un arco que corta al anterior.
- La recta que une los dos puntos de corte es la mediatriz del segmento que forman T8 y T9
- Repetimos la operación con el segmento que forman T9 y T12
- En el punto en que se cortan ambas mediatrices tenemos el centro de la circunferencia que pasa por T8, T9, y T12 al que vamos a llamar O6
- Con centro en O6 y radio igual al segmento que forman O6 y T9 trazamos la tercera de las ocho posibles circunferencias tangentes.
Cuarta circunferencia solución al problema de Apolonio
Ya tenemos tres de las ocho posibles circunferencias que proporcionan una posible solución al problema de Apolonio. Vamos a por la cuarta. Me vais a permitir, viendo lo largo que se está haciendo ésto, que a partir de ahora resuma los pasos. Si tenéis alguna duda, siempre podéis volver más arriba para repasar los pasos que hemos dado, porque los que siguen son repetición de ellos.
- Hallamos las mediatrices de los segmentos que forman T7, T10, y T11
- Donde se cortan tenemos el centro O7
- Con centro en O7 y radio igual al segmento que forman O7 y T11 trazamos la cuarta circunferencia tangente a las tres iniciales.
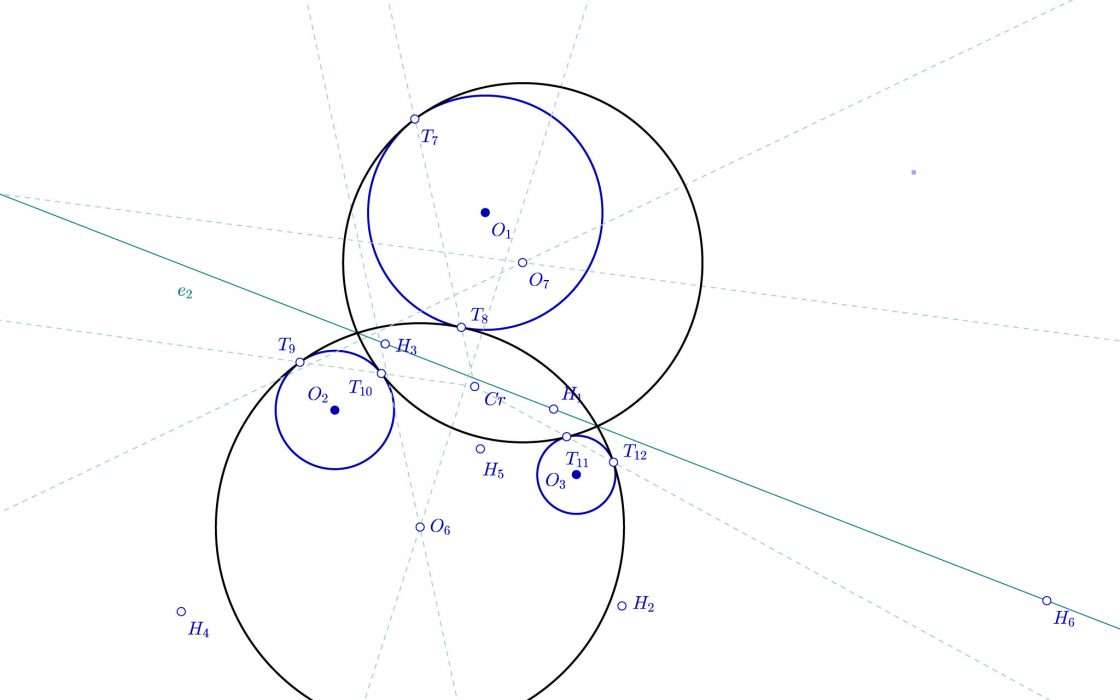
Llevamos cuatro de las ocho circunferencias posibles que serían la solución al problema de Apolonio. La cosa hasta el momento, haciendo limpieza de puntos y rayas quedaría así…
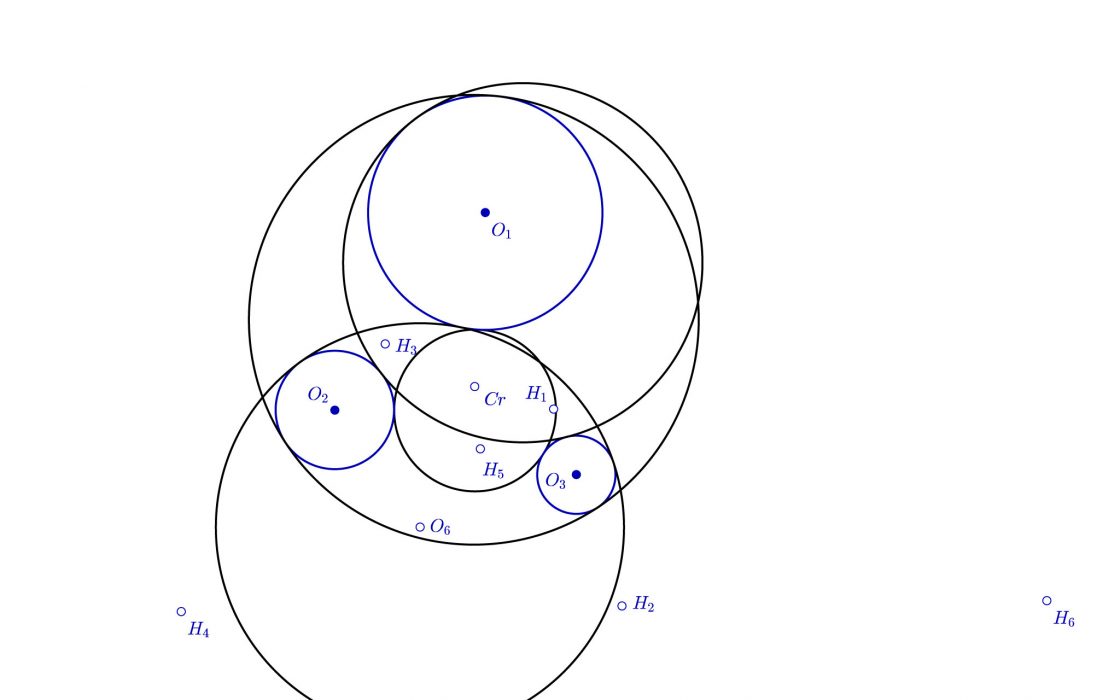
Solucionando el problema de Apolonio: Tercer par de circunferencias tangentes
Ya llevamos la mitad de la resolución del problema de Apolonio, pero tranquilos, que a partir de ahora iré más rápido. Si tenéis dudas repasar los pasos anteriores, porque lo que sigue es una repetición de lo que ya llevamos hecho.
- Trazamos el eje e3 uniendo los puntos de homotecia H3, H5 y H2
- Hallamos los polos de las circunferencias respecto a éste eje, a los que llamaremos Polo7 , Polo8 y Polo9
- Trazamos rectas desde el centro radical Cr que pasan por los polos, cortando a las circunferencias en T13, T14, T15, T16, T17 y T18
- Trazamos la circunferencia que pasa por T14, T15 y T18 y la que pasa por T13, T16 y T17
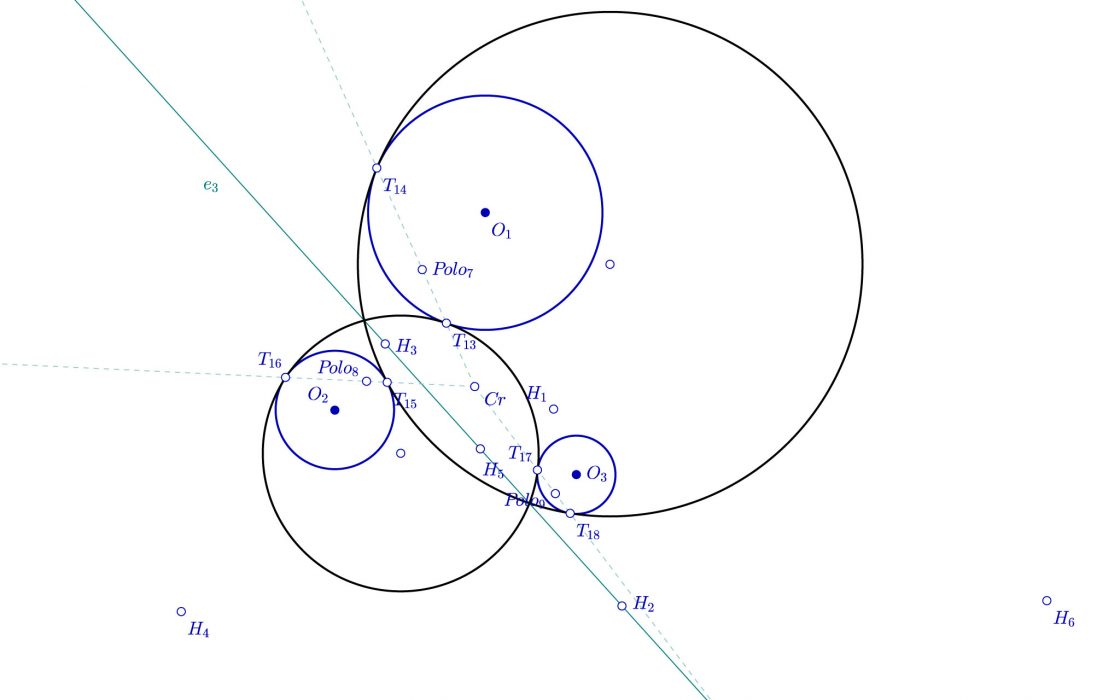
Si mostramos todas las que hemos solucionado hasta ahora, la cosa queda como se ve en la siguiente imagen.

Solución al problema de Apolonio: Último par de circunferencias tangentes
Vamos a por el último par de circunferencias que son la última solución que nos queda al problema de Apolonio.
- Trazamos el eje e4 que pasa por H1, H5 y H4
- Hallamos los polos de las tres circunferencias respecto a éste eje e4
- Realizamos las rectas que parten del centro radical y pasan por los polos, hallando los puntos de tangencia T19, T20, T21, T22, T23 y T24
- Trazamos las circunferencias que pasan por T20, T22 y T23 y por T19, T21 y T24
La cosa quedaría como sigue:
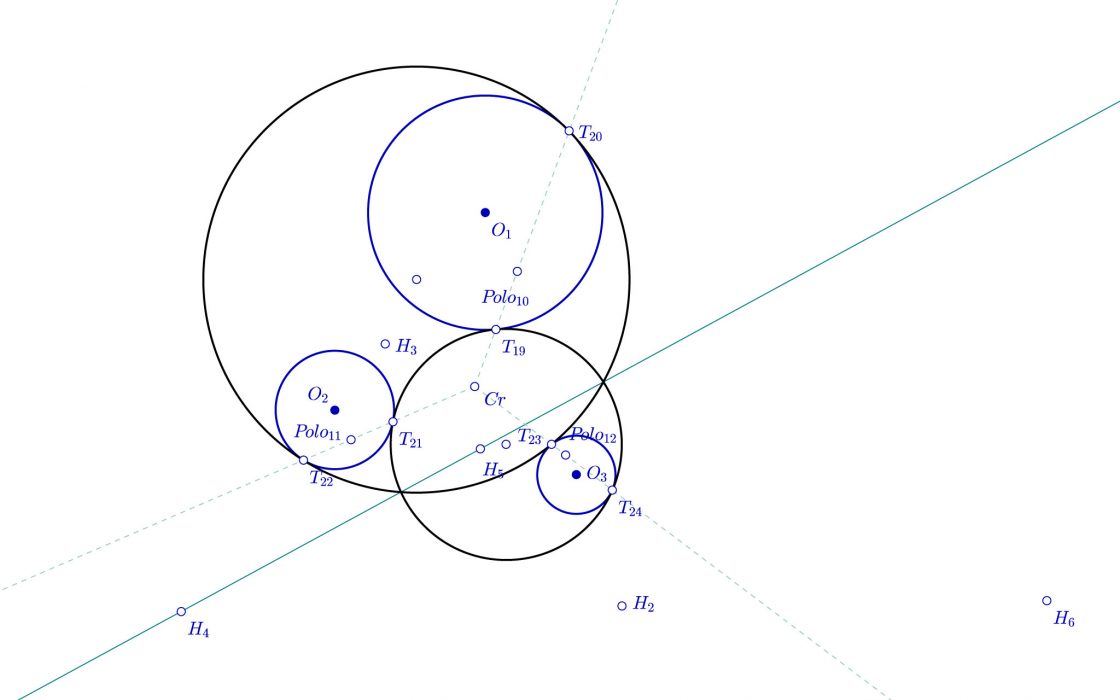
Con lo cual, las ocho circunferencias que son la solución al problema de Apolonio son las que veis en la imagen siguiente.

Y como regalo, si os gusta el arte abstracto, aquí os dejo una imagen con todas las rectas, perpendiculares, paralelas, puntos y circunferencias utilizados hasta llegar a ésta solución ? ? ?