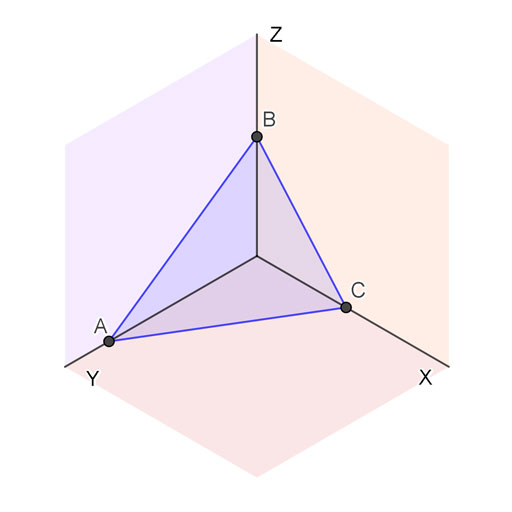
En el sistema de perspectiva axonométrica isométrica el plano se representa exactamente igual que en cualquier otro sistema de representación, a partir de tres puntos. Estos tres puntos se proyectan ortogonalmente sobre el plano del cuadro.
Aquí abajo tienes un plano básico, definido por la intersección de sus trazas con los ejes. Puedes mover los puntos A, B y C en las vistas en diédrico y estos se ajustarán de forma automática en su representación en isométrico. Los puntos de corte de las trazas del plano con los ejes o aristas del diedro determinan lo que se llama triángulo entre trazas.
Ejercicio práctico: Cómo dibujar un plano
Para ver como se dibujaría un plano, te propongo un ejercicio muy sencillo. En la siguiente aplicación tienes una figura muy básica, de la cual te enseñaré como dibujar un solo plano, el que aparece en azul. Este punto está definido por los puntos A, B y C. En la parte izquierda tienes las vistas diédricas, y a la derecha tienes la figura resuelta. Más abajo tienes el proceso paso por paso.
Lo primero de todo es dibujar los ejes. Si no recuerdas como, deberías visitar la entrada donde explico los fundamentos de la perspectiva isométrica. Para continuar, vamos a considerar que el vértice inferior derecho de la parte trasera coincide con el centro de coordenadas. De esa manera será más fácil dibujar la figura (además es lo más normal).
- Vamos a marcar el punto A en primer lugar. ¿Qué dimensiones tiene? Si te fijas bien, contando desde el centro de coordenadas (punto O) tiene 3cm de alto (eje Z), 9cm de ancho (eje Y) y carece de profundidad (eje X). Para marcarlo mide pues 9cm sobre el eje Y. De esa manera obtienes el punto A1.
- Realiza una paralela al eje Z (el de la altura) y mide sobre él los 3cm que tiene A de alto. De ese modo tienes el punto A. Como carece de profundidad, no tiene más complicación.
- Ahora te toca hallar B. Sobre el eje Y mide la anchura (3cm), de esa manera tienes B1.
- Traza una paralela al eje Z que pase por B1, y sobre él mide los 3cm que tiene de alto. De esa manera tienes B2.
- Continúa dibujando una paralela al eje X que pase por B2, y a partir de ese punto mide la profundidad del punto B. En este caso 6cm. De esa manera tienes el punto B.
- Para terminar, hay que hallar C. Sobre el eje Y mide la anchura (3cm) y de esa manera obtienes C1. Date cuenta de que coincide sobre B1 porque tanto C como B tienen la misma anchura.
- El siguiente paso es trazar una paralela al eje Z que pase por C1. A partir de ese punto debes medir la altura del punto C, que en este caso mide 9cm. Como el punto C carece de profundidad, no necesitas hacer pasos adicionales.
- Uniendo A, B y C, tienes la representación del plano que forman.
Posiciones del plano en perspectiva isométrica
A continuación tienes las posiciones más características que puede ocupar el plano en el sistema isométrico.
Plano oblicuo con el triángulo entre trazas en el primer diedro
Los puntos de corte de las trazas con los ejes arrojan un valor positivo. Aquí abajo puedes mover los puntos A, B y C para modificar la posición del plano.
Plano oblicuo con el triángulo entre trazas en el segundo diedro
Para este tipo de planos la traza sobre el eje Y tiene un valor negativo. Las trazas sobre los ejes X y Z tienen un valor positivo. Aquí abajo puedes mover el punto C para modificar la posición del plano.
Plano con el triángulo entre trazas en el cuarto diedro
En este caso, el plano tiene su traza sobre el eje X con un valor negativo, mientras que las trazas sobre los ejes Z e Y tienen un valor positivo. Aquí abajo puedes mover el punto A para modificar la posición del plano.
Plano con el triángulo entre trazas en el quinto diedro
La traza vertical de este plano (con el eje Z) tiene un valor negativo. Por otra parte, las trazas sobre los ejes X e Y (anchura y profundidad) tienen un valor positivo. Aquí abajo puedes mover el punto A para modificar la posición del plano.
Planos paralelos a las caras del diedro
Este tipo de planos son muy comunes a la hora de representar figuras en perspectiva axonométrica isométrica. Existen los tres siguientes.
Plano paralelo al plano horizontal (XOY)
Todos los puntos de este plano tienen la misma altura (coordenada Z). Por ese motivo tanto la traza vertical, como la traza sobre el plano de perfil serán paralelas a la línea de tierra. Carece de traza sobre el plano horizontal, al ser paralelo al mismo.
Aquí abajo puedes mover el punto P para modificar la altura del plano.
Plano paralelo al plano vertical (YOZ)
Los puntos de este tipo de planos tienen todos la misma coordenada X (profundidad). Por este motivo la traza horizontal es paralela a la línea de tierra (eje Y). La traza sobre el plano de perfil es perpendicular a la línea de tierra (eje X). Carece de traza sobre el plano vertical, al ser paralelo a este. Aquí abajo puedes mover el punto P para modificar la profundidad del plano α (coordenada sobre el eje X).
Plano paralelo al plano de perfil (XOZ)
Las trazas de este tipo de planos son perpendiculares a la línea de tierra (eje Y). Tanto la traza vertical, como la traza horizontal. Todos los puntos de este tipo de planos tienen la misma anchura (coordenada Y), por lo que carece de traza sobre el plano de perfil, al ser paralelo a él. Aquí abajo puedes mover el punto P para variar la coordenada Y del plano.
Planos oblicuos que son perpendiculares a las caras del diedro
Planos oblicuos perpendiculares al plano vertical
Estos planos tienen la traza horizontal perpendicular a la línea de tierra (eje Y). La traza en el plano de perfil es una línea paralela a la línea de tierra (eje X). La traza en el plano vertical es oblicua. Aquí abajo puedes mover los puntos A y B para ver cómo son este tipo de planos.
Plano oblicuo perpendicular al plano de perfil
Este tipo de planos tienen las trazas sobre el plano vertical y el plano horizontal paralelas a la línea de tierra. La traza sobre el plano de perfil es oblicua. En la aplicación que tienes debajo puedes modificar los puntos A y B para ver como se comportan las trazas de este tipo de planos.
Plano oblicuo perpendicular al plano horizontal
En los planos perpendiculares al plano horizontal las trazas sobre los planos vertical y de perfil son perpendiculares a la línea de tierra (representada en isométrico por los ejes X e Y). La traza sobre el plano horizontal (XOY) es oblicua.
Planos que contienen a uno de los ejes
Planos que contienen al eje X
Este tipo de planos son una posición particular de los planos oblicuos perpendiculares al plano vertical. Su traza sobre el plano horizontal coincide con la línea de tierra (eje X en isométrico). Del mismo modo, su traza sobre el plano de perfil coincide también con la línea de tierra, representada también por el eje X en isométrico.
Planos que contienen al eje Y
Estos planos son una posición particular de los planos perpendiculares al plano de perfil. Tanto la traza sobre el plano horizontal, como la traza sobre el plano vertical se encuentran sobre la línea de tierra. En isométrico coincide con el eje Y.
Planos que contienen al eje Z
Estos planos son una posición particular de los planos perpendiculares al plano horizontal. En este caso, tanto la traza sobre el plano de perfil, como la traza sobre el plano vertical coinciden sobre el eje Z. Es decir, una perpendicular a la línea de tierra que pasa por el centro de coordenadas.
Plano perpendicular al plano del cuadro
Este tipo de planos tienen la peculiaridad de que todas sus trazas son coincidentes en la vista en isométrico. En las vistas en diédrico, sus trazas siempre formarán un ángulo de 120 grados. Aquí abajo tienes un caso particular de éste tipo de planos. Se trata del plano perpendicular al plano del cuadro que además pasa por el centro de coordenadas. Puedes mover los puntos A1 y A2 para ver como se comportan las trazas del mismo también en diédrico.
