Parábola

Dentro de las distintas curvas cónicas posibles, nos encontramos la parábola. A continuación os explicaré toda la información imprescindible sobre éste tipo de curvas y algunos de los ejercicios más comunes que os encontraréis.

Definición de parábola

La parábola se define como una curva cónica plana, abierta y de una única rama. Se define como el lugar geométrico de los puntos del plano que equidistan de un punto fijo F, denominado foco, y de una recta fija d, llamada directriz.

Tiene un vértice V y un eje de simetría que pasa por V y que es perpendicular a la directriz d. La recta tangente en el vértice es paralela a la directriz d.

Elementos de la parábola

Los elementos de la parabola que debemos conocer son los siguientes:

Eje: Es la recta perpendicular a la directriz. Sobre el se sitúan tanto el foco como el vértice de la parábola. La parábola es siempre simétrica respecto al eje.
Vértice: Es el punto de la parábola que se sitúa sobre el eje y que es equidistante tanto del foco como de la recta directriz. Es el punto de la parábola que más próximo se encuentra a la recta directriz.
Radios vectores: son las rectas que unen un punto con el foco y la directriz.
Circunferencia focal: Es la recta directriz, tiene por tanto, radio infinito.
Parámetro: Es la longitud de la cuerda perpendicular al eje en el foco

Construcción por puntos

Se conocen la directriz d, el eje e y el foco F dela parábola. El vértice V será el punto medio del segmento OF. Si no conoces el eje, solo tienes que dibujar una perpendicular a la directriz que pase por F. Tu punto de partida debe parecerse a ésto:

En primer lugar, marca varios puntos sobre el eje, en el ejemplo de más abajo los he llamado A, B y C. Esos puntos no pueden estar entre O y V, porque si no, no podrás construir la parábola.
Dibuja una perpendicular al eje por el punto C.
Con el compás, mide la distancia entre O y el punto C. Usando esa misma distancia como radio, dibuja un arco con centro en F. Donde ese arco corta a la perpendicular, tienes los puntos C₁ y C₂
Repite el mismo proceso con los puntos B y A, de esa manera obtienes los puntos A₁, A₂, B₁ y B₂
Uniendo todos estos puntos, podremos trazar la parábola buscada.

Aquí abajo tienes el desarrollo en un vídeo explicativo, por si tienes alguna duda.

Construcción de la parábola conocidos el eje, el vértice y un punto de la curva

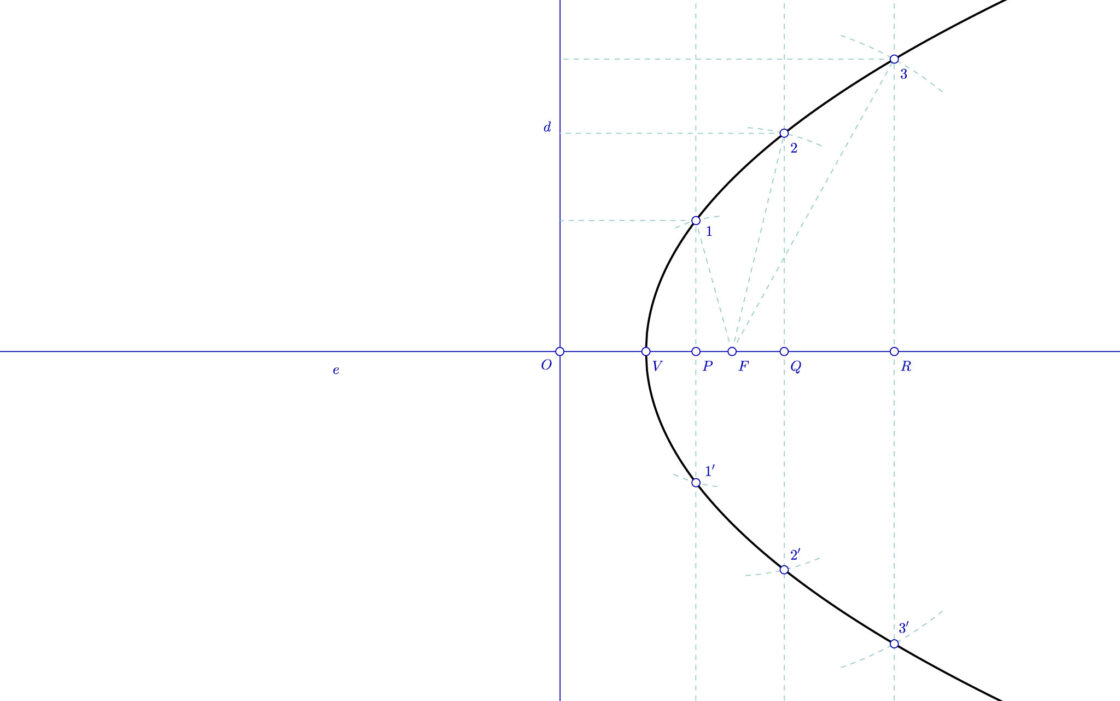
En esta ocasión los datos que conoces son el eje, el vértice y un punto P de la parábola. Tu punto de partida será semejante a lo que ves a continuación.

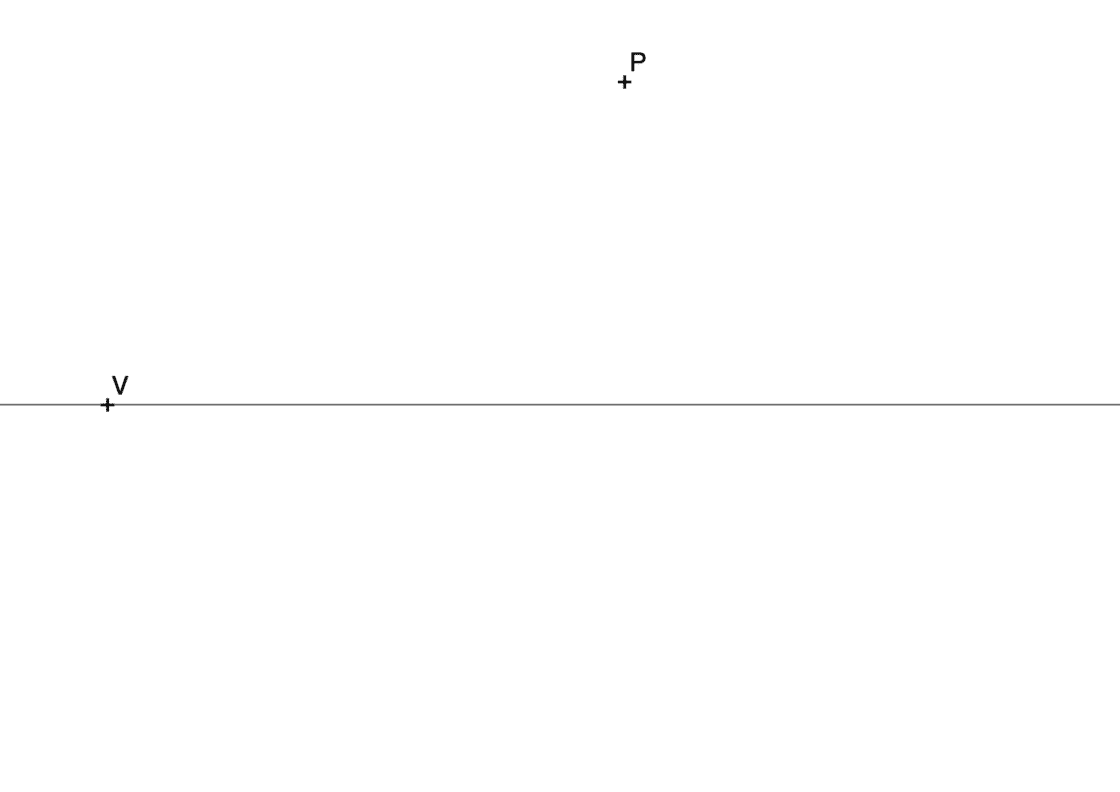
Trazamos la recta perpendicular al eje por el vértice, a la que denominaremos r
Dibujamos una recta paralela al eje por el punto P que corta a la perpendicular r en el punto R
Se dividen los segmentos RP y RV en el mismo número de partes usando el Teorema de Tales. En mi caso he dividido dichos segmentos en cuatro partes, obteniendo los puntos 1, 2, 3 y sus homólogos 1′, 2′ y 3′.
Trazamos segmentos que unen 1, 2 y 3 con V.
Dibujamos paralelas al eje por 1′, 2′ y 3′.
Donde el segmento V1 corta a la paralela que pasa por 1′ tendremos el punto A₁. Donde V2 corta a la paralela que pasa por 2′ tendremos el punto B₂, y así sucesivamente.
Por simetría, usando el compás y con centro en V, hallaremos los puntos A₂, B₂, C₂ y P’.
Si unimos todos éstos puntos tendremos la parábola buscada.

Si necesitas una aclaración más precisa, aquí abajo te dejo un vídeo donde puedes ver todo el proceso detallado paso a paso.

Trazar una parábola conociendo el vértice y el foco.

Este caso es semejante al primero de ésta página, lo único que necesitas para resolverlo es recordar que la distancia que tienes del foco al vértice es la misma que tienes del vértice a O, y por tanto la recta directriz. Ten en cuenta que el eje contiene tanto al vértice como al foco, por lo que es fácil hallarlo. que no te líen si te ponen este mismo ejercicio en vertical o en diagonal, se resuelve exactamente igual. Tu punto de partida será semejante a ésto:

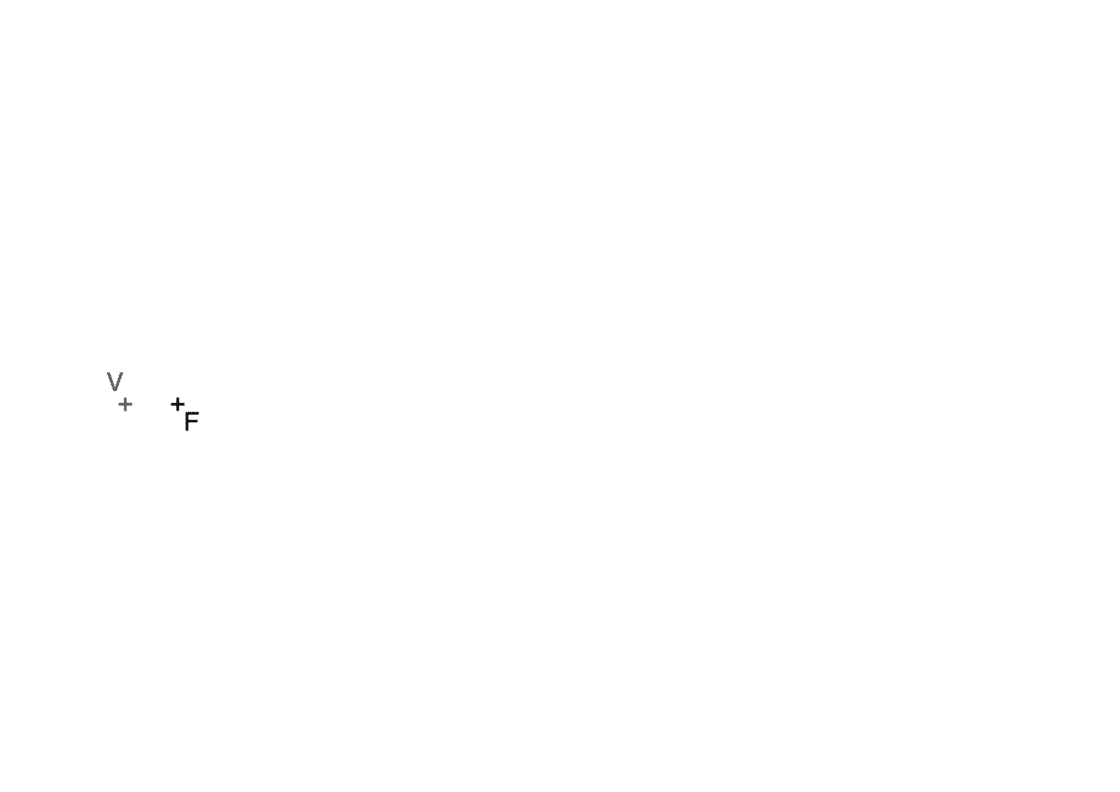
En primer lugar, traza una línea que una V y F. Esta línea es el eje.
Acto seguido, con el compás pincha en V, abre hasta F y luego marca sobre el eje al otro lado. Ese punto será O.
Traza una recta perpendicular al eje que pase por O. Esa será la directriz.

Para resolver el ejercicio, solo tienes que revisar el primer ejercicio de ésta página, ya que el desarrollo es el mismo.

Trazado mediante envolventes

En este tipo de ejercicios se suele proporcionar la directriz y el foco, el vértice y el foco, el foco y la recta tangente que pasa por el vértice, o alguna combinación parecida. En cualquier caso, necesitaremos saber la recta tangente que pasa por el vértice y el foco. Si no los sabemos, el primer paso es hallarlos.

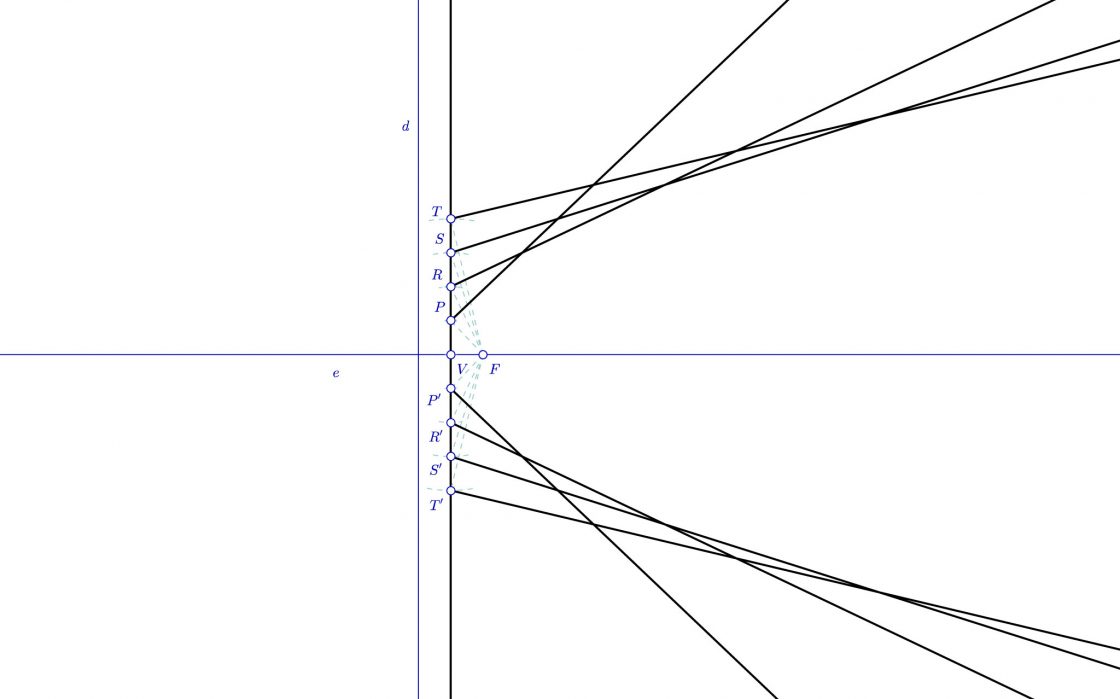
Cualquier recta tangente a la parábola cortará a la tangente que pasa por el vértice en un punto P que siempre formará un ángulo de 90 grados respecto al segmento que forman el punto P y el foco F.

Sabiendo ésto, solo tenemos que marcar puntos (aleatorios o no), sobre la tangente al vértice. Luego trazaremos perpendiculares a los segmentos que unan estos puntos con el foco. En este ejemplo he añadido cuatro puntos a los que he llamado P, R, S y T, y he calculado sus simétricos para dibujar la parte inferior de la parábola.

Ayúdame a mejorar esta entrada

¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti. Gracias de antemano por dejar tu comentario un poco más abajo.

«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.