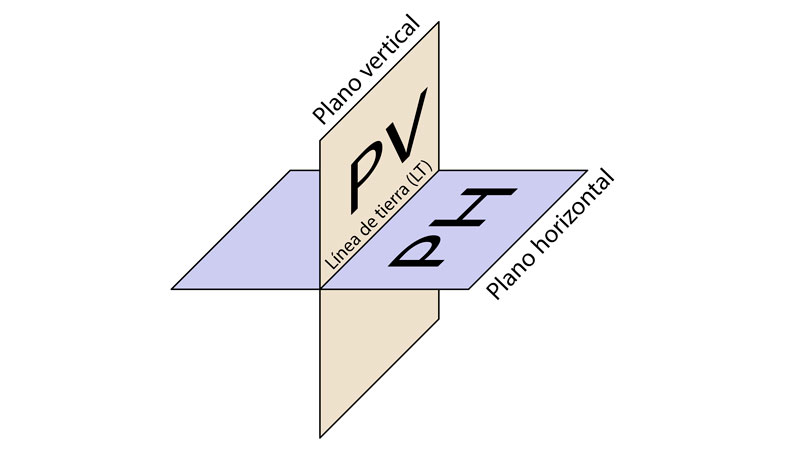
El sistema diédrico se basa en las proyecciones de los puntos sobre dos planos de proyección ortogonales (es decir, que forman 90º). Uno horizontal al que llamamos PH o Plano de proyección horizontal, y otro vertical al que se denomina PV o Plano de proyección vertical.
Conocer bien éste sistema es muy importante. Ten en cuenta que gracias a él podrás realizar representaciones en otros sistemas espaciales, como en perspectiva cónica frontal, cónica oblicua, axonométrico, etc.
Estos planos son opacos, ilimitados y forman entre si un ángulo de 90º. El lugar donde se cortan se denomina Línea de tierra o LT.

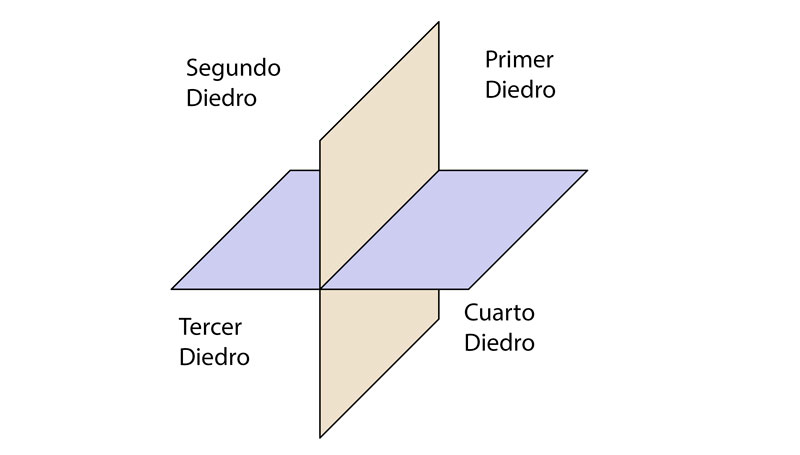
Los planos vertical y horizontal dividen en el sistema diédrico el espacio en cuatro diedros o cuadrantes, que se denominan 1erD, 2oD, 3erD, 4oD. O lo que es lo mismo… 1er Diedro o cuadrante, 2o Diedro o cuadrante, etc. Como podéis ver en el dibujo siguiente, se les numera en sentido contrario al movimiento de las agujas del reloj.
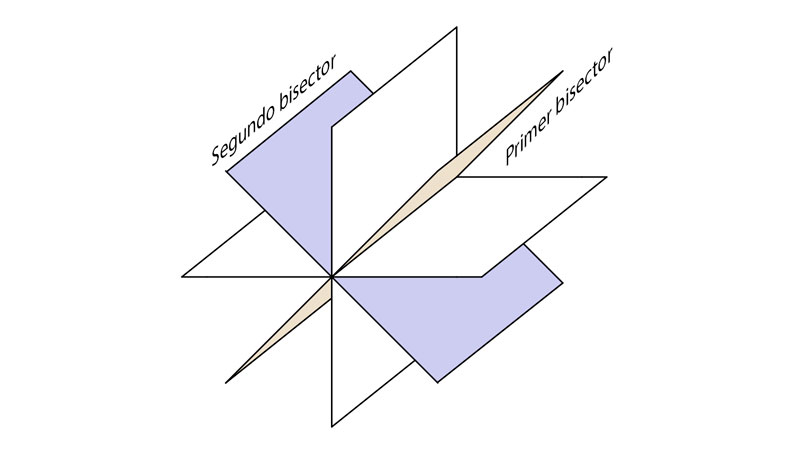
Estos cuadrantes a su vez son divididos cada uno de ellos en dos partes iguales por los llamados planos bisectores, dividiendo el espacio en ocho partes iguales llamadas octantes. Hay que recordar que los planos bisectores son solo dos, cortando el primer bisector al primer diedro y al tercer diedro, y el segundo al segundo diedro y al cuarto diedro.
El punto de vista siempre se sitúa dentro del primer diedro, por lo que la parte de las figuras que se encuentren en los otros tres se considera que está oculto.
Representación y proyecciones del punto en el sistema diédrico
Los puntos en el sistema diédrico se representan gracias a sus proyecciones. Podemos distinguir principalmente dos proyecciones, la vertical y la horizontal. En ocasiones también se utiliza la proyección lateral o de perfil.
La proyección sobre el plano horizontal se denomina proyección horizontal o planta. Se suele representar con una letra mayúscula acompañada del signo de prima (A’) o del número 1 en subíndice (A1).
Cuando hablamos de la proyección sobre el plano vertical ó PV, se denomina proyección vertical o alzado. Se suele identificar con una letra mayúscula acompañada de dos signos de prima (A») o bien con una letra mayúscula seguida del número dos en subíndice (A2).
En el sistema diédrico, cuando hablamos de alejamiento o distancia, nos referimos a la distancia que separa un punto cualquiera del plano vertical. Si queremos referirnos a su altura respecto al plano horizontal ó PH hablaremos entonces de altura o cota. En cualquier caso, ambos valores pueden ser tanto positivos como negativos.
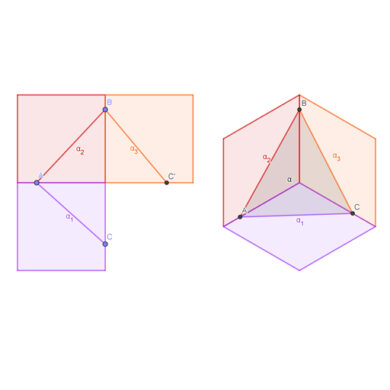
La línea donde se unen ambas proyecciones se llama línea de referencia del punto, y tiene la característica de que sean cuales sean las proyecciones del punto, siempre es perpendicular a la línea de tierra. Aquí abajo puedes mover los puntos B y C para plegar el espacio diédrico y ver como se vería en su representación tridimensional.
Para queremos representar un punto (que es tridimensional) en el papel (un espacio bidimensional), tenemos que abatir los planos. La tercera proyección sería A″′(vale, eso igual ya empieza a parecer excesivo), aunque yo personalmente prefiero la denominación de una letra mayúscula acompañada del número 3 en subíndice (A3). Ese tercer plano se denomina plano de perfil o PP.
A continuación te ofrezco una pequeña aplicación interactiva que espero que te aclare las ideas. Puedes mover las proyecciones del punto A, representadas por sus proyecciones en diédrico A1 y A2. También puedes mover el punto P para plegar los planos. De esa manera puedes alternar entre el espacio tridimensional (es una perspectiva caballera) y el espacio bidimensional que representaría el folio donde dibujamos en diédrico.
Posiciones del punto en el sistema diédrico
Un punto puede ocupar infinitas posiciones en el espacio. A continuación te explicaré los más representativos que te puedes encontrar en cualquier ejercicio del sistema diédrico.
Puntos situados en los diedros o cuadrantes
Tal como te explicaba un poco más arriba, en el sistema diédrico el espacio se divide en cuatro diedros o cuadrantes. Así pues, habría cuatro tipos distintos de posición.
Puntos situados en el primer diedro
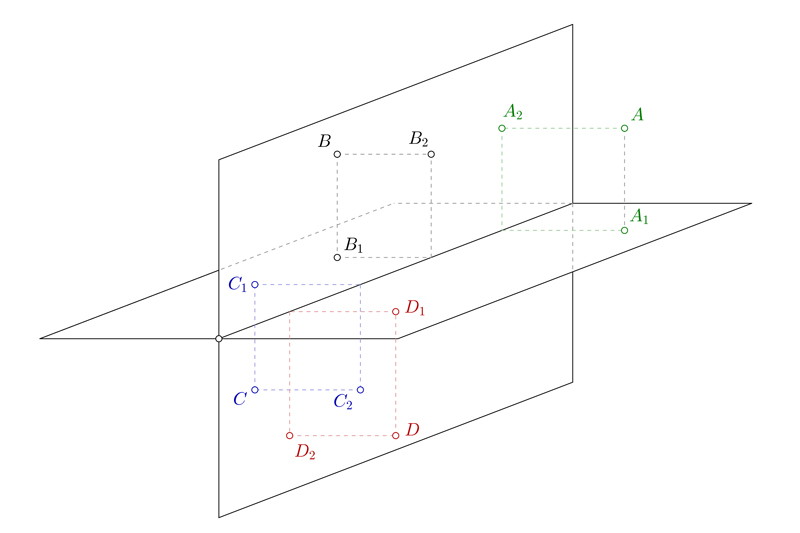
Éste tipo de puntos tienen su traza vertical por encima de la línea de tierra, y la traza horizontal debajo de la misma. En la imagen se representa por el punto A y sus trazas A1 y A2
Puntos situados en el segundo diedro
Cuando un punto se encuentra en el segundo cuadrante, sus dos proyecciones se encuentran sobre la línea de tierra. En la imagen se representa por el punto B y sus proyecciones B1 y B2
Puntos que se encuentran en el tercer cuadrante
Para éste tipo de puntos, sus proyecciones se encuentran invertidas. Es decir, la traza vertical se encuentra por debajo de la línea de tierra, y la traza horizontal se encuentra sobre la misma. En la imagen se representa por el punto C, y sus proyecciones C1 y C2
Puntos sobre el cuarto cuadrante
Los puntos que se encuentran en el cuarto diedro o cuadrante tienen sus dos proyecciones bajo la línea de tierra. En la imagen se representa por el punto D y sus proyecciones D1 y D2
Puntos contenidos en los planos bisectores
Éstos puntos tienen las mismas características y propiedades que los anteriores, pero con la peculiaridad de que tanto su cota como su alejamiento son iguales. Esto da lugar a que los puntos que se encuentran en el segundo y cuatro diedro tengan sus proyecciones sobre el mismo punto.
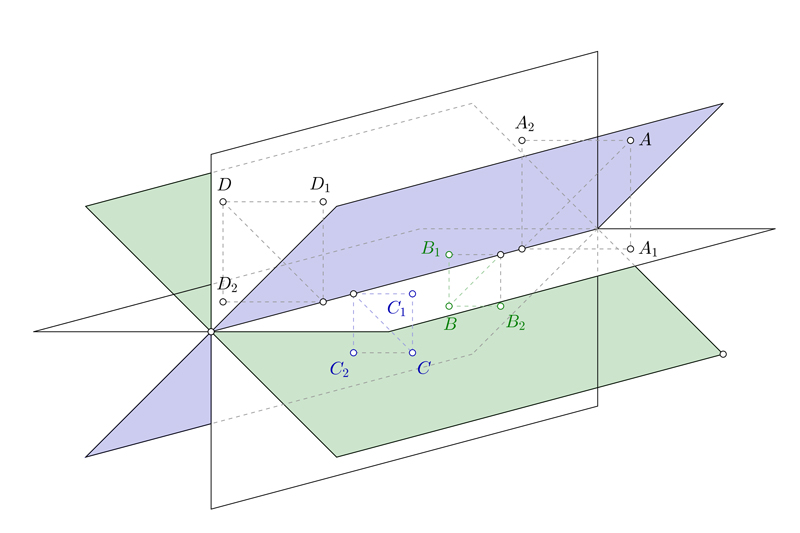
En la siguiente imagen puedes ver que los puntos A y B se encuentran en el primer bisector, y los puntos C y D sobre el segundo bisector.
Puntos sobre los planos de proyección del sistema diédrico o la línea de tierra
En ésta ocasión te puedes encontrar con cinco tipos distintos de posición en el sistema diédrico. En cuatro de ellos se encuentran sobre los planos de proyección (anterior o posterior. En el último caso, el punto se encuentra sobre la propia línea de tierra.
Puntos sobre el plano horizontal
Pueden estar por delante del plano vertical, o por detrás del mismo. En ambos casos la proyección vertical se encontrará sobre la línea de tierra. La cota o altura de éstos puntos es siempre igual a cero.
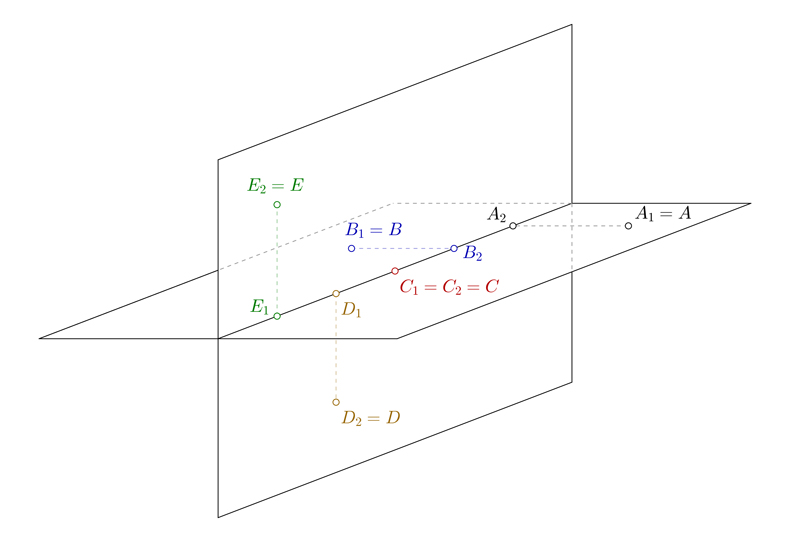
Cuando se encuentran delante del plano vertical, su proyección se representa debajo de la línea de tierra. Por otra parte, si se encuentran detrás del plano vertical, su proyección estará por encima de la línea de tierra. En la imagen se representan por los puntos A y B y sus trazas. Como puedes ver, las proyecciones verticales coinciden con el propio punto.
Puntos sobre la línea de tierra
Cuando los puntos se encuentran sobre la línea de tierra, tanto su altura o cota, como su alejamiento o profundidad, es cero. Sus dos proyecciones se encuentran sobre la línea de tierra y coinciden con el propio punto. En la imagen se representa por el punto C.
Puntos sobre el plano vertical
Los puntos que se encuentran sobre el plano vertical tienen su proyección horizontal sobre la línea de tierra. Su traza vertical puede encontrase por encima o por debajo del plano horizontal. Cuando se encuentran por encima, su proyección estará por encima de la línea de tierra. Por otra parte, cuando se encuentran por debajo, su proyección también lo estará. En cualquier caso, su proyección vertical siempre coincide con el propio punto. En la imagen los tienes representados por los puntos D y E con sus proyecciones.
Glosario de puntos en sistema diédrico
En la siguiente imagen tienes un resumen rápido de los posibles tipos de puntos que puedes encontrar. Voy a detallarlos para que los identifiques.
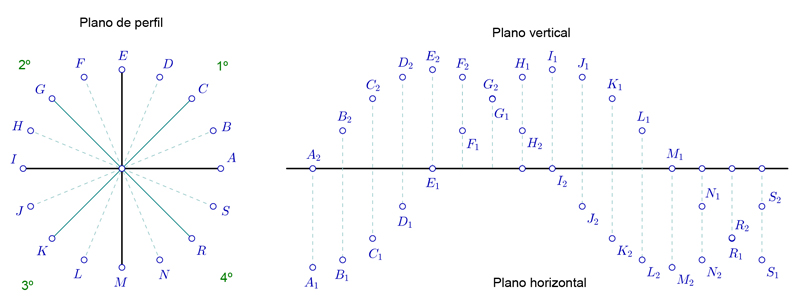
- Puntos en el primer diedro: BCD. El punto C se encuentra además sobre el primer plano bisector.
- Puntos sobre el plano vertical: E, sobre la línea de tierra, en la parte superior. M bajo la línea de tierra, en la parte inferior.
- Puntos en el segundo diedro: FGH. De ellos, G se encuentra además en el segundo plano bisector.
- Puntos sobre el plano horizontal: I, que está en la parte posterior, tras el plano vertical. A, que está por delante del plano vertical, en la parte delantera.
- Puntos en el tercer diedro: J, K, L. El punto K se encuentra además en el primer plano bisector.
- Puntos en el cuarto diedro: N, R, S. Sobre el segundo plano bisector nos encontramos al punto R.
- Punto sobre la línea de tierra: No lo he representado. En el plano de perfil se encontraría en la intersección del plano vertical y horizontal. Sus proyecciones horizontales y verticales se encuentran sobre la línea de tierra.
Como dibujar la tercera proyección del punto
Para hallar la tercera proyección debes saber muy bien donde se encuentra el punto. El procedimiento es muy sencillo. Por la proyección vertical debes realizar una paralela a la línea de tierra. Por la proyección horizontal debes trazar una paralela que corte al plano de perfil. Este punto de corte lo debes abatir en sentido de las agujas del reloj si se encuentra en el primer o cuarto cuadrante, y en sentido contrario si está en el segundo o tercero. En la siguiente imagen tienes cuatro posibilidades distintas, un punto para cada diedro.
Representación del punto por coordenadas
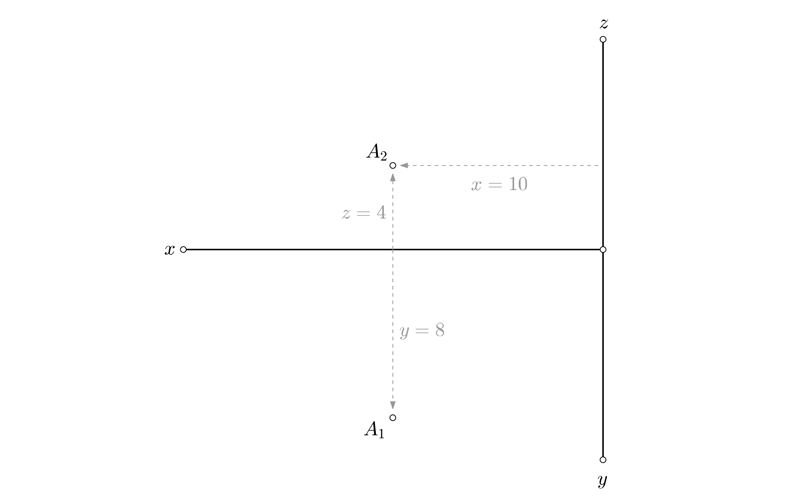
Una forma muy habitual de especificar la posición de los puntos en el sistema diédrico es por coordenadas. Es éste tipo de representaciones siempre se toman las tres dimensiones, y se usan los tres planos proyectantes como referencia. Para calcular las medidas, se toma el punto de intersección de los planos como punto cero.
La situación de cada punto se determina de la siguiente manera P(x, y, z) lo que viene a ser P(anchura, altura, profundidad). Dependiendo de donde se encuentre el punto, algunos de éstos valores pueden ser negativos.
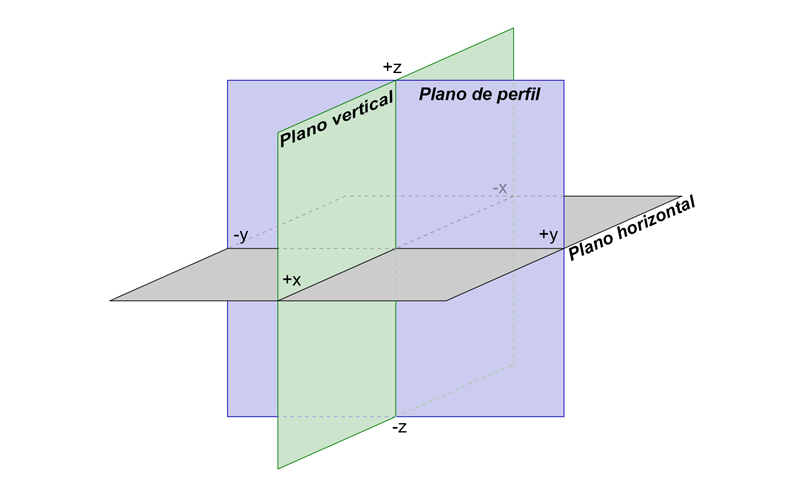
En la siguiente imagen tienes la representación de un punto de muestra, en éste caso sería A(10, 4, 8). Es decir, está separado 10cm del plano de perfil, 4cm sobre el plano horizontal, y alejado 8cm del plano vertical.
Ejercicio interactivo de puntos
Aquí abajo tienes una aplicación interactiva que puedes modificar para generar distintos problemas de ejercicios de puntos en sistema diédrico.
Para ver la solución, solo tienes que desplazar la imagen hacia la izquierda. La solución varía de forma automática según sitúes los puntos.
También te puede interesar…
25 enero, 2022
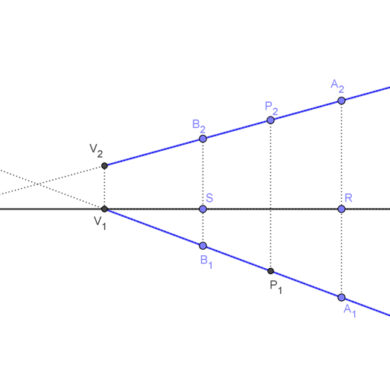
Representación de la recta en sistema diédrico
13 diciembre, 2021
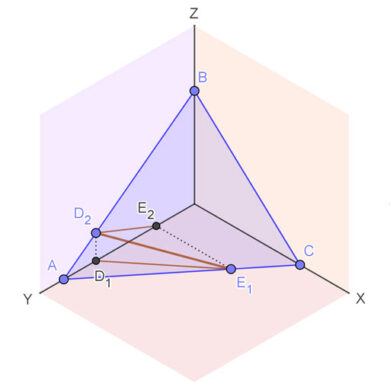
Pertenencias en sistema diédrico: punto, recta y plano
1 diciembre, 2021
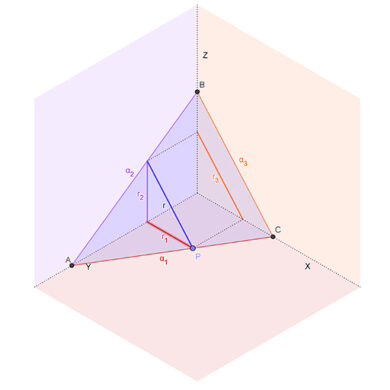
Rectas fundamentales en el plano
26 octubre, 2021
Representación del plano en sistema diédrico
10 noviembre, 2020
Tipos de rectas en diédrico
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti. Gracias de antemano por dejar tu comentario un poco más abajo.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
