
En ésta entrada te voy a enseñar las formas más habituales para dibujar polígonos regulares cuando conocemos el radio de la circunferencia circunscrita. Es decir, la circunferencia que contiene al polígono en cuestión. Este nivel es adecuado para primero de bachillerato. En otra entrada te explicaré como construir los polígonos cuando conocemos la longitud del lado. Pero ese tipo de ejercicios son un poco más complicados y están más indicados para un nivel de segundo de bachillerato.
Trazar un triángulo equilátero inscrito en una circunferencia
El enunciado suele ser algo como: «Dada la circunferencia de radio N, dibujar el triángulo equilátero incrito en la misma.» Otra posibilidad sería que te pidieran dividir la circunferencia en tres partes iguales. Al fin y al cabo, viene a ser el mismo ejercicio. Ya verás como éste ejercicio es el más sencillo de todos.
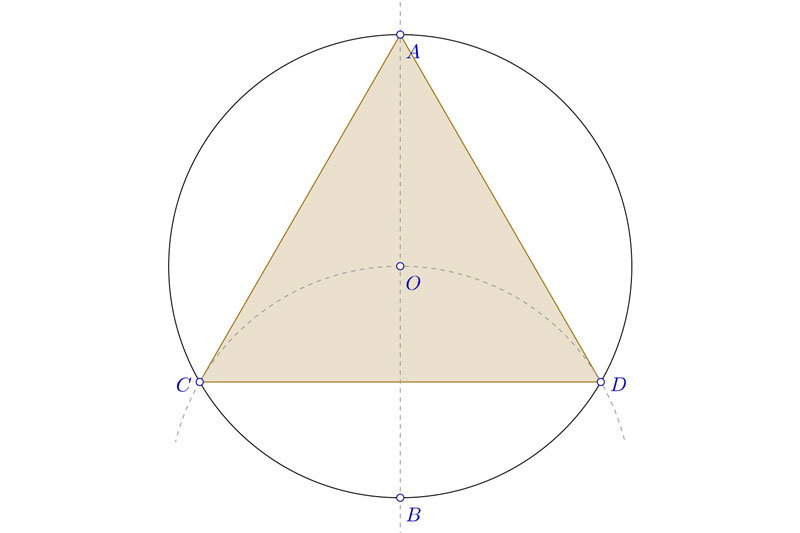
- Lo primero que tienes que hacer es dibujar una recta auxiliar que pase por el centro O de la circunferencia. De esa manera determinas los puntos A y B en los puntos de corte con la circunferencia.
- Acto seguido, pincha con el compás en B, y abriendo hasta O, traza un arco que corta en los puntos C y D a la circunferencia.
- Si unes A, C y D, tienes el triángulo equilátero que estás buscando.
Dividir una circunferencia en cuatro partes iguales
…o lo que viene a ser lo mismo, dibujar el cuadrado inscrito en la circunferencia. Si el ejercicio de antes te ha parecido sencillo, seguro que éste tampoco te va a hacer sudar.
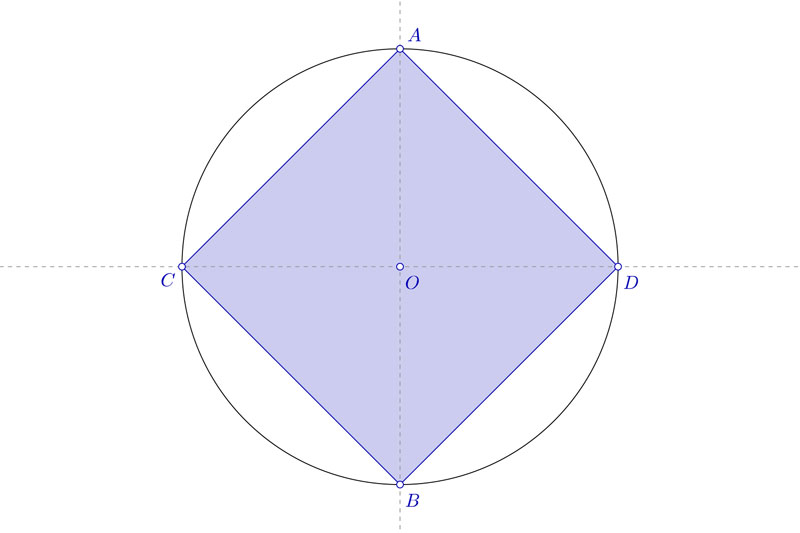
- Dada una circunferencia de radio N y centro O, lo primero que tienes que hacer es dibujar los ejes. Recuerda que deben ser dos rectas perpendiculares que pasan por el centro O.
- Los puntos donde cortan a la circunferencia los llamaremos A, B, C y D.
- Si unes esos puntos, tendrás el cuadrado inscrito, o lo que es lo mismo, habrás dividido la circunferencia en cuatro partes iguales.
Dibujar un pentágono regular
Otra forma de plantear ejercicio sería dividir la circunferencia en cinco partes iguales.
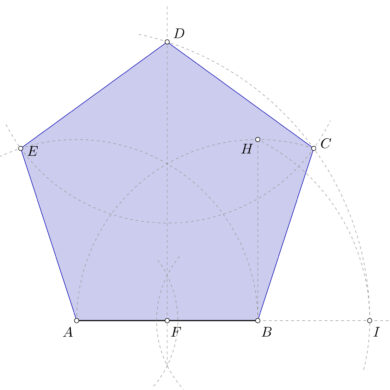
- Lo primero que tienes que hacer es dibujar los ejes de la circunferencia, ya que sobre ellos vamos a encontrar algunos puntos que necesitarás más adelante.
- Una vez dibujados los ejes, tienes que hallar el punto medio de la longitud del radio. Para ello puedes dibujar la mediatriz. El punto de intersección con el eje te marca el punto A.
- Con el compás, con centro en A y radio hasta el vértice superior (que vamos a llamar B) tienes que dibujar un arco que corta al eje en el punto C.
- Con centro en B y radio hasta C, debes dibujar un arco que corta a la circunferencia en el punto D.
- El segmento BD nos está indicando la longitud del lado. Si prolongas ese arco, te cortará en el punto E, que también es uno de los vértices del pentágono.
- Con esa misma medida, con centro en D y en E, dibuja dos arcos que cortarán a la circunferencia en F y H. Esos puntos son los últimos vértices del pentágono.
- Si unes B, D, E, F y H tendrás el pentágono que estás buscando.
Dividir una circunferencia en N partes iguales
Seguro que estabas esperando que aquí te explicara como dibujar el hexágono regular, o como dividir una circunferencia en seis partes iguales. Pero voy a ir más allá. Te voy a explicar como hallar cualquier polígono cuyo número de lados sea múltiplo de uno de los tres anteriores; 6, 8, 10, 12, 16. 20…
El proceso es realmente sencillo, para ello solo tienes que hallar el lado del polígono más básico. Es decir, 3, 4 ó 5. Luego haces la mediatriz de ese lado, y donde corte a la circunferencia tendrás la nueva medida. La siguiente imagen creo que te lo aclarará rápidamente.
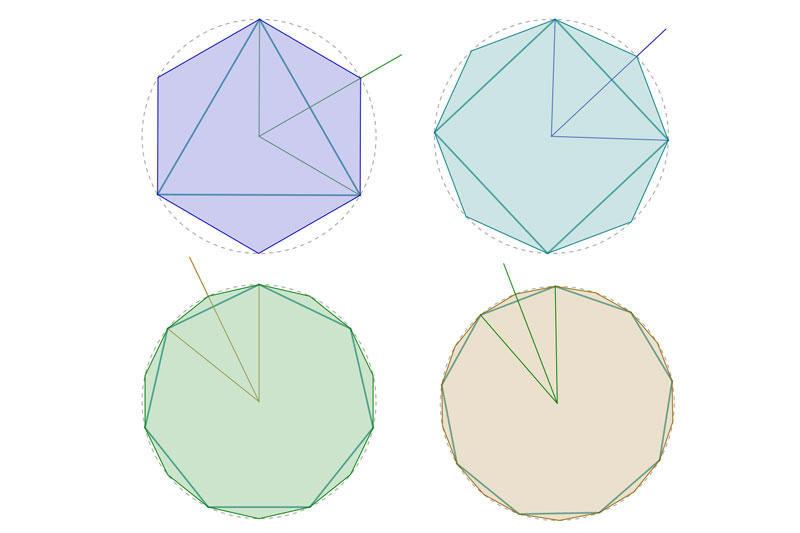
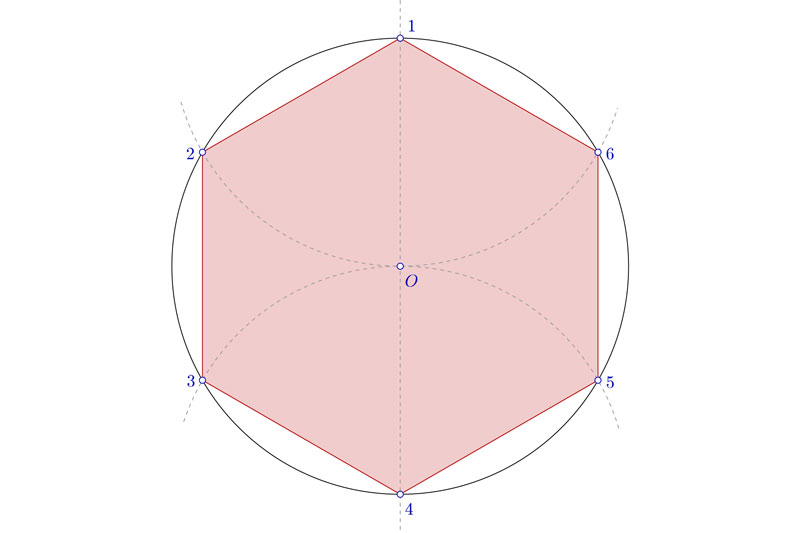
De todas formas, el hexágono es el más sencillo de todos, ya que no es necesario hallar la mediatriz. Arriba te lo he puesto como ejemplo, pero no es necesario. Es tan sencillo que no me voy a molestar ni en transcribirlo, te voy a poner una imagen y solo con verla, estoy seguro de que lo vas a pillar al vuelo.
Dibujar un heptágono regular
Un heptágono es un polígono de siete lados. Antes de nada, te tengo que aclarar que éste método no es perfecto. En éste tipo de ejercicios siempre hay un lado que es distinto de los demás. Si somos muy precisos y pulcros trabajando, ésta diferencia no tiene porqué notarse, no obstante. Yo de todas formas, siempre recomiendo dibujar los lados de forma simétrica. Uno a la derecha, otro a la izquierda, de manera que el lado desigual nos quede en la base. De esa manera el resultado queda mucho más presentable.
- En primer lugar tienes que dibujar la mediatriz del radio. Si te fijas, este paso es igual que en el pentágono. De esa manera determinas el punto A.
- Esa mediatriz corta a la circunferencia en el punto B.
- Si unes A con B, ese segmento mide la longitud del lado del polígono que queremos dibujar.
- Mide la longitud de AB con el compás, y con centro en el vértice superior (al que he llamado E en el vídeo), tienes que dibujar un arco que cortará a la circunferencia en los puntos C y D.
- Repite la operación. Con esa misma medida, y tanto con centro en C, como con centro en D, realiza dos arcos que cortarán a la circunferencia en los puntos F y H.
- Una vez más, con centro en F y H, dibuja dos arcos con la misma distancia que en el paso anterior. De esa manera hallarás los puntos I y J, que son los últimos vértices que te faltan para terminar la figura.
- Si unes E, C, D, F, H, I y J, ya tienes el heptágono regular que te piden solucionar.
Trazar el eneágono inscrito en una circunferencia
El eneágono es el polígono de nueve lados. En éste caso, te piden dibujarlo y el único dato que conoces es el radio de la circunferencia que lo contiene (circunferencia circunscrita).
- Empieza dibujando los ejes de la circunferencia, que necesitarás enseguida.
- Sobre esos ejes marca el punto A, y con radio de A hasta O, dibuja un arco que corta a la circunferencia en el punto B.
- Ahora marca el punto C, y con centro en C y radio hasta B, traza un arco que cortará a la prolongación del eje en el punto D.
- Dale la vuelta al compás, porque necesitas esa misma medida. Pinchas en D, y dibujas un arco que cortará al eje vertical en el punto E.
- Al vértice superior del eneágono lo vamos a llamar F. Pues bien, la longitud del segmento FE te está indicando cuando mide el lado del eneágono.
- Con centro en F y radio FE, dibuja un arco que corta en los puntos H e I.
- Ahora solo tienes que seguir el proceso, utilizando esa misma medida para marcar todos los vértices del eneágono y así solucionar éste ejercicio.
Dibujar un nonágono (método preciso)
Por si aún no lo sabes, nonágono y eneágono significa lo mismo. Nonágono proviene del latín y eneágono proviene del griego, pero se refieren al polígono regular de nueve lados. El método anterior es aceptado en cualquier examen de acceso a la universidad o parecido. No obstante, si quieres conocer un método todavía más preciso, te lo voy a explicar a continuación, aunque te adelanto que es bastante más complejo.
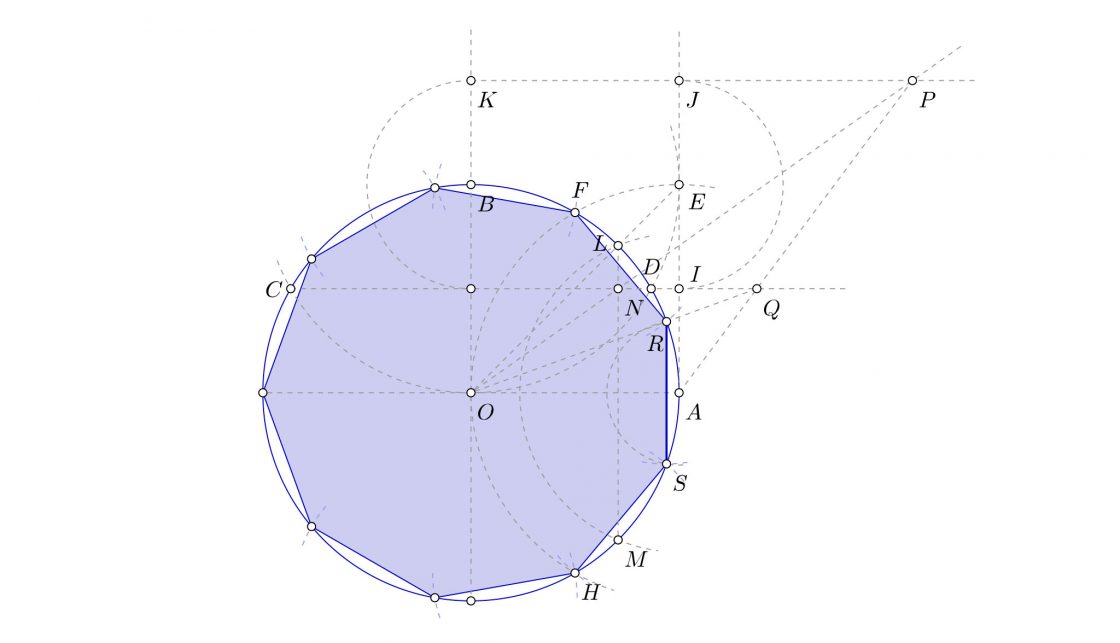
- Empieza por dibujar los ejes, los vas a necesitar para los pasos siguientes.
- Traza una paralela al eje vertical por el punto A.
- Con centro en A y radio hasta O, dibuja un arco. Desde B y también con radio hasta O, traza un arco que corte al anterior. Los puntos de corte que te interesan los vas a llamar C, D, E, F y H.
- Realiza una recta que pasa por C y D, cortará a la paralela al eje en el punto I.
- Con centro en E y radio hasta I, traza un arco que corta a la paralela al eje en el punto J. Con ese mismo radio, pero con centro en B, traza otro arco que cortará a la prolongación del eje en el punto K.
- Traza la recta que pasa por J y K.
- Dibuja la bisectriz del ángulo de 90 grados. Es decir, la recta que une O con E. Esta recta corta a la circunferencia en el punto L.
- Con centro en A, y radio hasta L, dibuja un arco que cortará a la circunferencia en el punto M.
- Une L con M, en el punto de corte con la recta que va de C a D tienes el punto N.
- Dibuja la recta que va de O hasta el punto N y prolóngala hasta cortar a la recta que pasa por J y K. A ese punto de intersección lo llamaremos P.
- Une el punto A con el punto P, al punto de intersección de la prolongación de la recta que pasa por C y D llámalo Q.
- Dibuja la línea que va de O a Q. Este segmento corta a la circunferencia en el punto R.
- Traza un arco con centro en A y radio hasta R. Este arco cortará a la circunferencia en el punto S.
- El segmento que va de R a S es la longitud del lado del nonágono regular.
Método genérico para hallar un polígono de N lados
¿Te has preguntado que pasa cuando tienes que dibujar un polígono regular con un número de lados primo? ¿O un múltiplo de tres? El undecágono, por ejemplo. Por si no lo sabes, el undecágono es el polígono regular de once lados. Mucho ojo, porque éste método NO SE DEBE USAR para hallar polígonos que se pueden hallar mediante la mediatriz de un lado, como el de 8, 10, 12, etc.
Pues hay un método para todos ellos. Es relativamente sencillo, no te asustes. De todas formas, es obligatorio conocer el Teorema de Tales, porque forma parte del proceso.
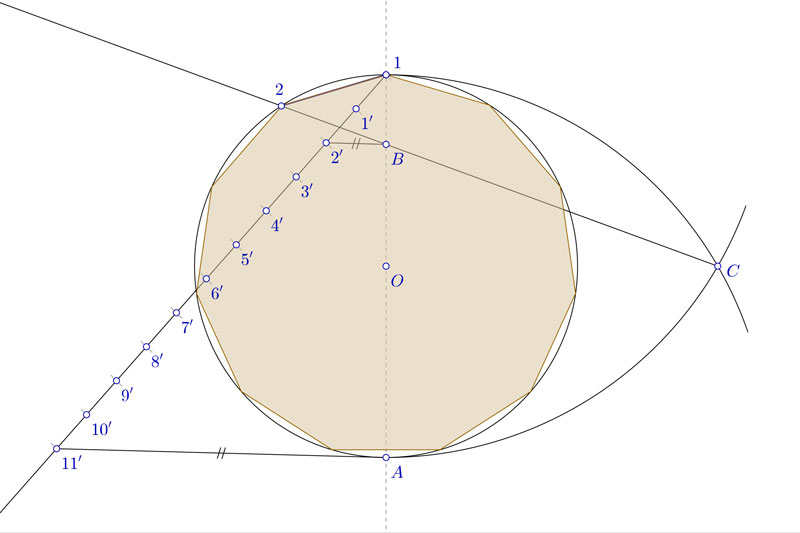
- Dada la circunferencia, lo primero que tienes que hacer es dibujar el eje vertical (el otro te da igual, no lo vas a necesitar.
- Marca el vértice superior. Para tenerlo identificado, llámalo 1. Es el primer punto del polígono. El punto donde corta en la parte inferior no es un vértice, pero lo necesitarás más adelante. Llámalo A, por ejemplo.
- Ahora, usando el Teorema de Tales, debes dividir el diámetro en un número de lados igual al número de lados que tendrá tu polígono. En concreto te interesa el segundo punto empezando desde arriba. Vamos a llamarlo B para identificarlo.
- Con centro en A, y radio hasta 1, dibuja un arco. Con esa misma medida, con centro en 1, y radio hasta A, dibuja otro arco que cortará al anterior en un punto al que llamaremos C.
- Traza la línea que parte de C y pasa por B. El punto donde corta a la circunferencia lo puedes llamar 2.
- El segmento que une los puntos 1 y 2 es la medida del lado del polígono que buscas.
Recuerda que el último lado es diferente de los demás. No mucho, pero si no usas un buen compás, se notará bastante. Por eso recomiendo marcar los lados de forma paralela. Uno a la derecha, otro a la izquierda. De esa manera el lado irregular quedará abajo y no se notará tanto.
También te puede interesar…
15 septiembre, 2021
Equivalencias – Construcción de figuras y polígonos equivalentes
16 junio, 2021
Dibujar polígonos regulares sabiendo el lado
20 octubre, 2020
Polígonos regulares
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti. Gracias de antemano por dejar tu comentario un poco más abajo.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
