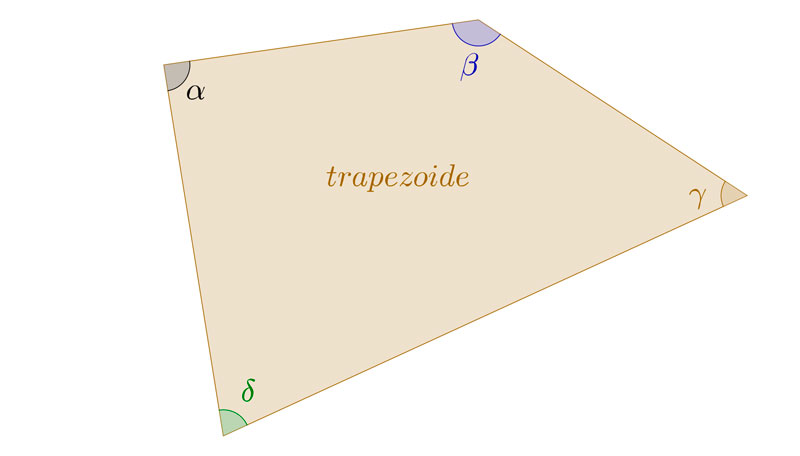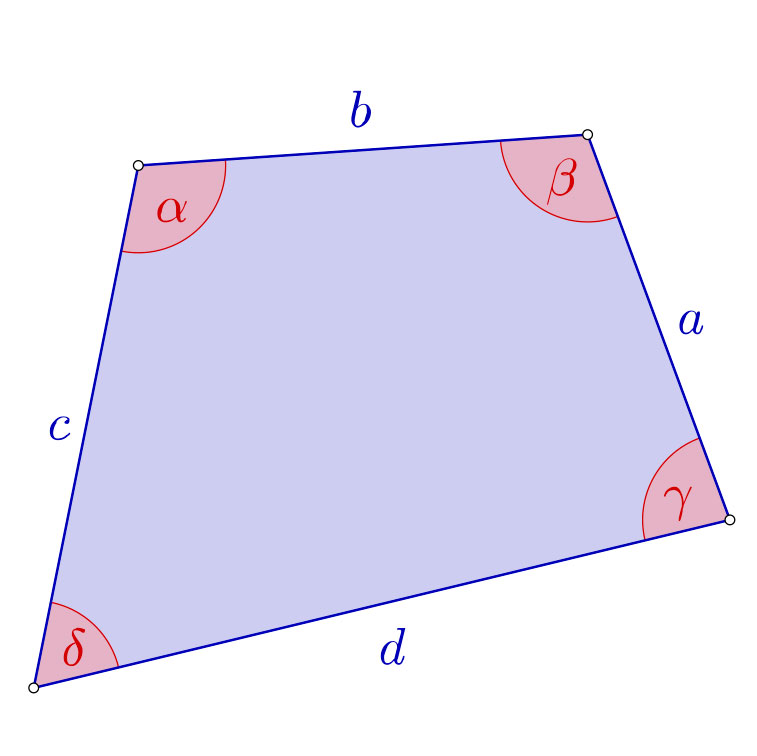
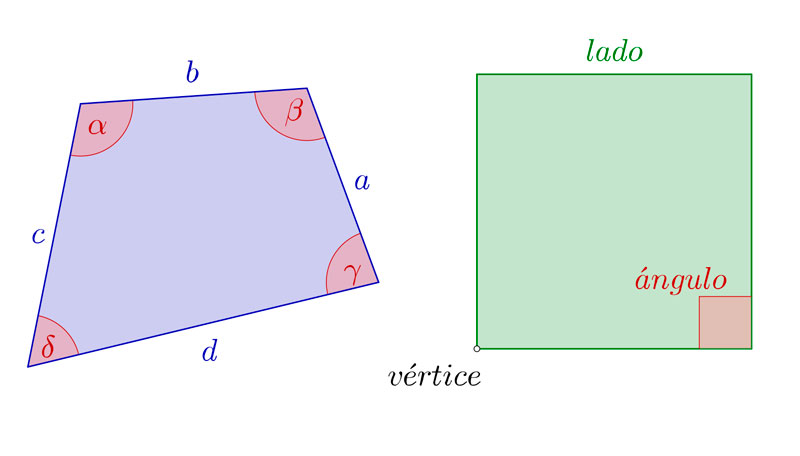
La definición más sencilla de los cuadriláteros sería: Polígonos formados por cuatro rectas que se cortan dos a dos, con cuatro ángulos. La manera de denominar sus distintas partes es igual que la que hacíamos con los polígonos regulares y con los triángulos. Los puntos de intersección de las rectas son los vértices, y los segmentos entre los vértices son los lados.
Clasificación de los cuadriláteros
Dependiendo de la longitud de sus ládos y ángulos, y de la relación existente entre ellos, podemos establecer una clasificación en tres tipos distintos: paralelogramos, trapecios y trapezoides. Vamos a ver las propiedades de cada uno de ellos.
Paralelogramos
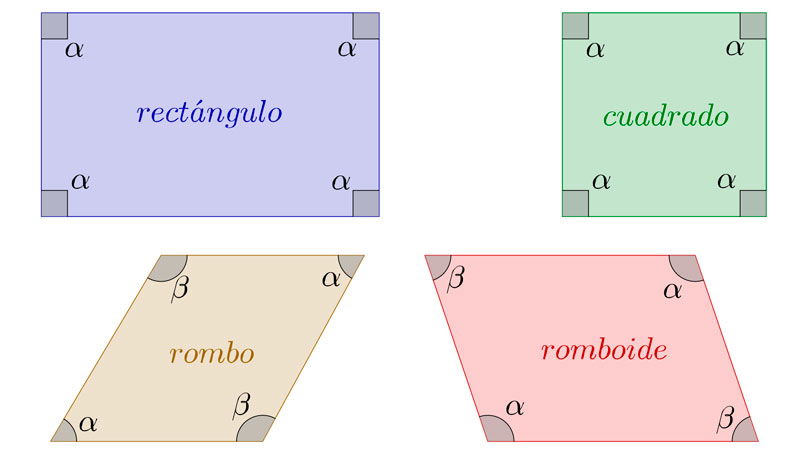
Los paralelogramos se distinguen porque tienen sus lados paralelos entre si dos a dos, y sus ángulos interiores son también iguales dos a dos. En base a ésta definición podemos realizar una nueva división de los paralelogramos en cuatro tipos distintos: cuadrados, rectángulos, rombos y romboides.
Cuadrado
De entre todos los cuadriláteros, el cuadrado es el único paralelogramo regular que existe. Todos sus lados son iguales entre si. Sus ángulos también son los cuatro iguales y forman un ángulo de 90º siempre. Además, se da la propiedad de que sus diagonales son iguales entre si y perpendiculares la una a la otra.
Rectángulo
El rectángulo posee todos los ángulos iguales entre si, midiendo 90 grados cada uno de ellos. Las diagonales son iguales entre si y oblicuas. Sus lados son iguales dos a dos, siendo paralelos los lados con la misma medida. Es un polígono irregular porque sus lados no miden todos lo mismo.
Rombo
El rombo posee todos sus lados iguales. Sus ángulos son iguales dos a dos, dos agudos y dos obtusos. Sus diagonales son distintas y perpendiculares entre si, habiendo siempre una de mayor longitud que se denomina diagonal mayor y una más corta que se suele llamar diagonal menor. Al igual que el rectángulo, el rombo es un polígono irregular porque sus ángulos no son todos iguales.
Romboides
Los romboides son cuadriláteros que tienen los lados iguales dos a dos. Los lados que son iguales entre si siempre se encuentran separados y son también paralelos. Sus ángulos son también iguales dos a dos, encontrándose opuestos aquellos que son iguales. Las diagonales son distintas y oblicuas.
Cuadriláteros trapecios
Los trapecios son cuadriláteros que tienen solo dos lados paralelos entre si. A estos lados se les llama bases. Dependiendo de la longitud de sus lados y ángulos los clasificamos en rectángulos, isósceles y escalenos. Si te fijas, reciben la misma nomenclatura que los triángulos. Y si prolongaramos sus lados, podríamos construir un triángulo que a su vez sería también rectángulo, isósceles o escaleno.
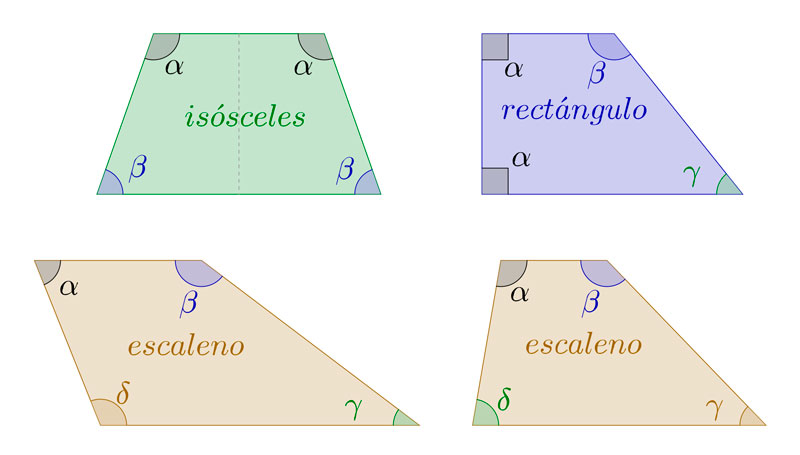
Trapecio isósceles
Podemos decir que son trapecios isósceles todos aquellos cuadriláteros que tienen los lados que no son paralelos entre si iguales. Además, sus ángulos son iguales dos a dos. Siendo dos agudos y dos obtusos. Tiene asimismo un eje de simetría que parte a la figura en dos mitades iguales. Si prolongamos sus lados, dibujaríamos un triángulo isósceles.
Trapecio rectángulo
Un trapecio rectángulo es un cuadrilátero que tiene un lado perpendicular a ambas bases. Por ese motivo, dos de sus ángulos son rectos, es decir, de 90 grados. Estos ángulos rectos serán siempre adyacentes. Si prolongamos sus lados, dibujaremos un triángulo rectángulo.
Trapecio escaleno
Será trapecio escaleno todo aquel cuadrilátero que no cumple ninguna de las propiedades anteriores. Sus bases son paralelas entre si, pero de distinta longitud. Sus lados son también de distinta longitud, así como sus diagonales. Sus angulos son también distintos entre si. Si prolongamos sus lados, dibujaremos un triángulo escaleno.
Cuadriláteros trapezoides
Los cuadriláteros trapezoides tienen todos sus lados y ángulos distintos entre si. Además ninguno de sus lados es paralelo a otro. Por supuesto, son polígonos irregulares.