Doy por sentado que ya sabes como dibujar los ejes en perspectiva isométrica, y como dibujar puntos y líneas. Si no es así, te recomiendo que leas antes los artículos en los que hablo sobre la perspectiva isométrica y el coeficiente de reducción, el punto y la línea en isométrica.
Antes de empezar, una pequeña aclaración… Para dibujar un círculo, se trate del sistema de representación que se trate, necesitarás al menos ocho puntos del mismo. En este caso cuatro de ellos los puedes hallar fácil, ya que son los puntos de tangencia de la circunferencia con el cuadrado que la contiene. Es decir, donde los ejes de la circunferencia cortan al cuadrado. Eso es fácil porque no hay curvas de por medio.
Los otros puntos son lo que vas a hallar con este procedimiento. Son cuatro puntos que se encuentran sobre las diagonales. Podrías hallar más si quisieras, pero no suele ser necesario. Se utilizan estos porque son simétricos y dividen a la circunferencia en ocho partes iguales. Aparte de que es más fácil hallar las diagonales que cualquier otra línea.
Cómo dibujar círcunferencias en perspectiva axonométrica isométrica
Para simplificar la explicación, te recomiendo no aplicar el coeficiente de reducción. De todas formas, si necesitas aplicarlo, queda a tu elección. Para este ejercicio vamos a suponer que quieres dibujar un círculo en isométrica de un tamaño cualquiera. Por ejemplo 10cm.
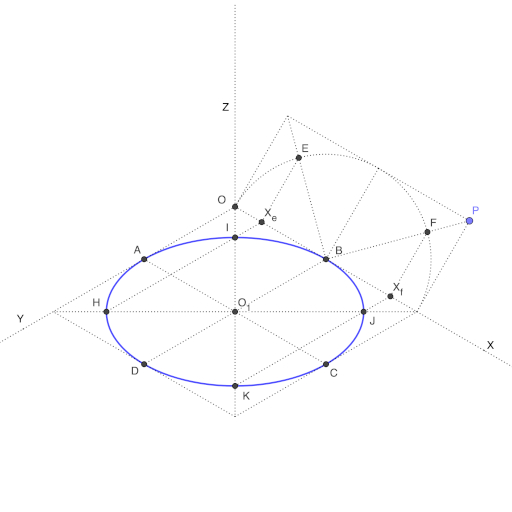
- Lo primero que debes hacer es dibujar el cuadrado que inscribe al círculo, en el lugar donde quieres dibujarlo. Para este ejemplo puedes dibujarlo en el plano del suelo directamente. Así pues, será un cuadrado de 10×10.
- A continuación dibuja las diagonales de la circunferencia. De esa manera obtienes el punto O1, que será el centro de la circunferencia.
- Ahora dibuja paralelas a los ejes X e Y que pasen por O. Eso marca los ejes de la circunferencia, y los puntos A, B, C y D serán los puntos de tangencia de la misma con el cuadrado. Esos puntos por lo tanto pertenecen a la circunferencia.
- Puedes continuar a partir del eje X o del eje Y. En este caso continuaremos a partir del eje X. Dibuja un arco con centro en B y radio hasta O. Este arco representará la circunferencia en diédrico, ya que lo que estamos haciendo es un cambio de plano.
- El siguiente paso sería dibujar sobre ese arco las diagonales. Una forma fácil es con la escuadra, midiendo ángulos de 45 grados a partir de B. Otra forma sería dibujar los dos cuadrados que contienen a ese arco a base de perpendiculares. Luego unirías B con los vértices de esos cuadrados. Los puntos donde esas líneas (las que forman 45 grados cortan al arco) tienes los puntos E y F.
- Dibuja perpendiculares al eje X que pasen por E y F. Donde cortan al eje te dan los puntos Xe y Xf.
- Ahora traza paralelas al eje Y que pasen por Xe y Xf
- Donde esas paralelas cortan a las diagonales del cuadrado que dibujaste en la planta tienes los puntos H, I, J y K.
- Si unes A, B, C, D, H, I, J y K tienes la elipse que determina esa circunferencia vista en perspectiva isométrica
Cómo hallar más puntos
Supongamos que has realizado todo el proceso anterior, pero por el motivo que sea quieres hallar más puntos de esa circunferencia (para tener más precisión). Llegados a éste punto date cuenta de que los segmentos HJ e IK determinan los ejes de una elipse. Así puedes realizar el proceso para dibujar una elipse una vez que conoces los ejes. De esa manera puedes obtener todos los puntos que quieras de forma rápida y fácil.
