En los triángulos existen una serie de rectas y puntos que es importante conocer, ya que gracias a ellos y a sus propiedades podremos hallar la resolución de ejercicios más complejos. En este apartado vamos a hablar del baricentro, del ortocentro, del incentro, y del circuncentro, los puntos notables de todo triángulo y de sus propiedades y características.
Baricentro y sus propiedades
Este punto lo hallaremos trazando las medianas desde cada vértice del triángulo hasta la mitad del lado opuesto. Como es lógico, en todo triángulo se pueden trazar tres medianas que se cortan en un punto concreto. Este punto es el baricentro.
Hay dos propiedades muy interesantes de éste punto. La primera se relaciona con el campo de la física, y consiste en que éste punto es el centro de gravedad. Su segunda propiedad consiste en que las medianas se cortan siempre en proporción de uno y dos tercios. Esto significa que el baricentro siempre está situado a dos tercios de los vértices, y a un tercio de los lados. El baricentro se suele marcar con la letra mayúscula G. Puedes practicar con el siguiente triángulo.
En la siguiente aplicación puedes mover los vértices A, B y C para comprobar estas propiedades.
Ortocentro y sus propiedades
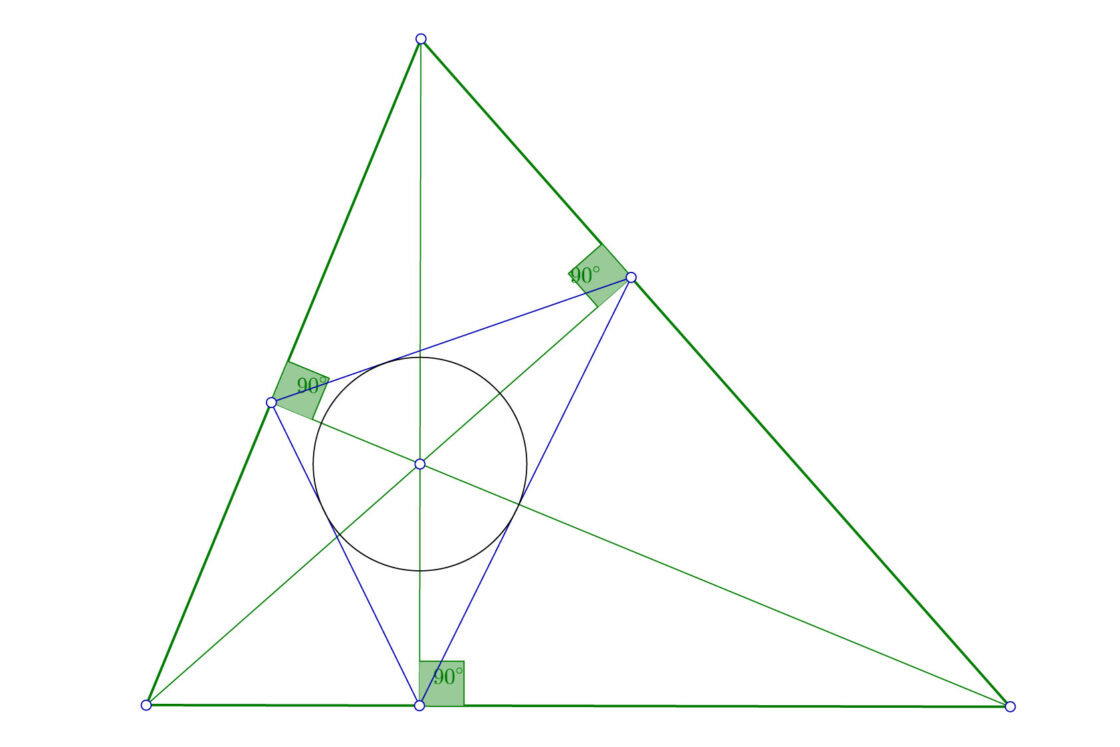
El punto donde se cortan las tres alturas del triángulo es lo que en geometría se denomina ortocentro. Éste nombre proviene del griego «orto» que significa «recto», en clara referencia al ángulo que forman las bases y las alturas. Recordemos que las alturas cortan en perpendicular a las bases.
Su propiedades más interesantes están con lo que se denomina triángulo órtico o triángulo pedal. Este triángulo lo podemos formar uniendo los pies de las tres alturas. En este caso, el ortocentro coincide además con el incentro del triángulo órtico. El ortocentro se suele nombrar mediante la letra mayúscula H. Puedes mover los puntos A, B y C para comprobar como se comporta el ortocentro y el triángulo órtico.
Como dato curioso, cuando se trata de un triángulo obtusángulo (que uno de los ángulos mide más de 90 grados) el ortocentro está fuera del triángulo. Puedes imprimir este triángulo para practicar este ejercicio.
Incentro y sus propiedades
Dentro de todo triángulo podemos dibujar una circunferencia que es tangente a los tres lados. Esto es lo que denominamos la circunferencia inscrita al triángulo. Su centro es lo que denominamos incentro del triángulo. Para hallar su centro y de ese modo poder dibujarla trazaremos las tres bisectrices de los tres ángulos del triángulo. El punto donde se cortan es el incentro. Puedes utilizar este triángulo para practicar.

Una propiedad muy interesante relacionada con las bisectrices, y por tanto con el incentro, es que las circunferencias exinscritas se encuentran en la intersección de las bisectrices con las de los ángulos exteriores del triángulo.
Circuncentro y sus propiedades
Si trazamos las mediatrices (recordemos que la mediatriz es una recta perpendicular que parte desde cada uno de los lados), el punto donde éstas se cortan es lo que llamamos circuncentro. Se suele denominar con la letra mayúscula O, y tiene la propiedad de ser el centro de la circunferencia circunscrita al triángulo. Puedes practicar con este triángulo.
Aquí abajo puedes mover los puntos A, B y C para verificar que siempre se cumplen las propiedades del circuncentro.
