Cuando hablamos del ángulo que forman una recta y un plano nos referimos al ángulo que forma la recta cuando se proyecta ortogonalmente sobre ese plano. Para comprenderlo un poco mejor, vamos a empezar con las situaciones más fáciles, es decir, hallar el ángulo que forma una recta cualquiera con los planos de proyección. Esto se puede averiguar fácilmente abatiendo la recta sobre el plano correspondiente.
Como hallar el ángulo que forma una recta oblicua con el plano horizontal
Para poder averiguar el ángulo que forma una recta con el plano horizontal necesitas dos puntos. Uno de ellos puede ser la propia traza de la recta sobre el plano horizontal, si es que la conoces. Si no, siempre puedes marcar dos puntos cualquiera sobre la recta para resolver este ejercicio. Tu punto de partida será algo parecido a esto:

¿Recuerdas el procedimiento para hallar la distancia entre dos puntos? Pues este procedimiento es el mismo. Consiste en abatir la recta de forma paralela al plano que nos interesa, en este caso el horizontal. La diferencia es que antes nos interesaba la distancia y ahora nos interesa el ángulo, pero el procedimiento es el mismo.
- Empieza calculando la diferencia de altura entre los dos puntos. Para ello dibuja una paralela a la línea de tierra. Esta paralela corta al segmento que une B1 y B2 en el punto C. La diferencia de alturas será la distancia entre C y B2. Para identificarla puedes llamarla h.
- Ahora dibuja una perpendicular al segmento que une A1 y B1 por uno de ellos, por ejemplo B1. Sobre esa perpendicular, a partir de B1 mide h. De esa manera obtienes D.
- El segmento que forman A1 y D representa el abatimiento del segmento que forman A y B sobre el plano horizontal. Por tanto, el ángulo que forman B1, A1 y D es el ángulo que forma la recta r con el plano horizontal.
Hay otra forma de resolver este ejercicio. Lo puedes resolver también girando la recta hasta que quede paralela al plano vertical. De esa manera podrás apreciar las verdaderas magnitudes sobre el plano vertical. Para que tengas más láminas con las que practicar, aquí tienes otro punto de partida distinto.

En este caso lo que hemos hecho ha sido girar la recta. La nueva posición será paralela al plano vertical. De esa manera, el ángulo que forman B2, E2 y C se observa en verdadera magnitud. Para que puedas comprobar que el procedimiento es correcto, aquí abajo tienes los dos procedimientos sobre el mismo supuesto. Como puedes ver, en ambos casos el resultado es el mismo. Puedes mover los puntos para verificarlo.
Ángulo que forma una recta oblicua con el plano vertical
Este ejercicio es prácticamente idéntico al anterior. La diferencia será que los puntos los hallaremos por diferencia de alejamientos en vez de por la diferencia de alturas o cotas. Aquí abajo tienes otra recta distinta para practicar con ella. Tu punto de partida será algo como esto.

Y aquí abajo tienes el procedimiento resuelto. No voy a entrar en detalles, se puede apreciar a simple vista que es prácticamente igual que el anterior, pero reflejando todos los pasos respecto a la línea de tierra.
Dibujar una recta que forme un ángulo α con el plano horizontal y un ángulo β con el plano vertical
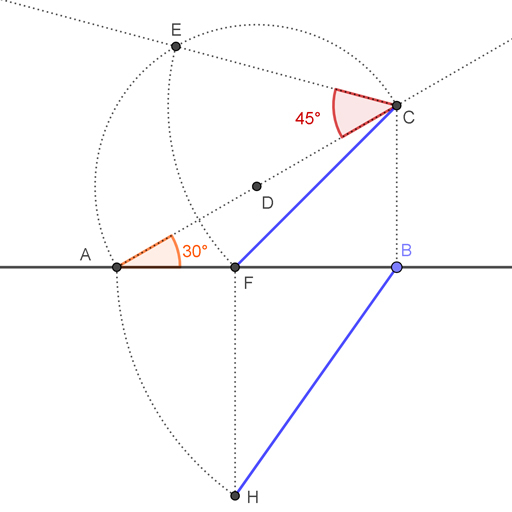
Para ponerle un valor concreto a los ángulos y poder realizar este ejercicio, vamos a considerar que el ángulo que forma con el plano horizontal es α y tiene un valor de 30º. Por otra parte, el ángulo que forma con el plano vertical es β y tiene un valor de 45º.
- Empieza dibujando la línea de tierra.
- Por un punto cualquiera A de la línea de tierra marca el ángulo α.
- Marca un punto B cualquiera y levanta una perpendicular por este punto hasta cortar a la recta que marca el ángulo α. Ese punto lo llamaremos C para identificarlo. Date cuenta de que donde estén A y B no importa, solo influirá en el tamaño final de la construcción, pero no en sus ángulos.
- Halla el punto medio entre A y C, que será D.
- Con centro en D, dibuja media circunferencia, donde A y C serán los extremos del diámetro.
- Ahora mide el ángulo β sobre el segmento AC. Donde ese ángulo corta a la semicircunferencia tienes el punto E.
- Continua dibujando un arco con centro en C y radio hasta E que corte a la línea de tierra en el punto F.
- Traza una perpendicular a la línea de tierra que pase por F.
- El siguiente paso será dibujar un arco con centro en B y radio hasta A que corte a la perpendicular del paso anterior. De esa manera obtienes el punto H.
- Para terminar, une C con F para obtener la proyección vertical de la recta, y B con H para hallar la proyección horizontal de la recta.
Aquí abajo tienes a la izquierda el procedimiento. Puedes mover los deslizadores para cambiar los ángulos. A la derecha tienes la demostración (usando los procedimientos que has visto más arriba) de que se cumplen los ángulos. Puedes mover el punto B para solapar ambas construcciones y verificar que son idénticas.
