La elipse es el lugar geométrico de los puntos del plano cuya suma de las distancias a otros dos puntos fijos que se suelen denominar como F y F’, llamados focos es constante. Ésta distancia es igual a la longitud de su eje mayor. Define un área curva, cerrada y plana con dos ejes de simetría que coinciden con sus ejes. Se produce al seccionar la curva cónica con un plano de tal manera que solo secciona a uno de los conos. A continuación tienes una aplicación interactiva para comprobarlo.
Propiedades de la elipse
Tiene dos ejes perpendiculares que se cortan en el punto medio O, que es el centro de la curva. El eje mayor AB se suele denominar eje real, y se representa por 2a. Se da la peculiaridad de que los focos de la elipse siempre están sobre este eje. El eje menor CD se representa por 2b. La distancia entre focos F-F’ se suele expresar como 2c.
Así pues, entre a, b y c siempre se cumple que a al cuadrado es igual a la suma de b al cuadrado y de c al cuadrado.
Radios vectores
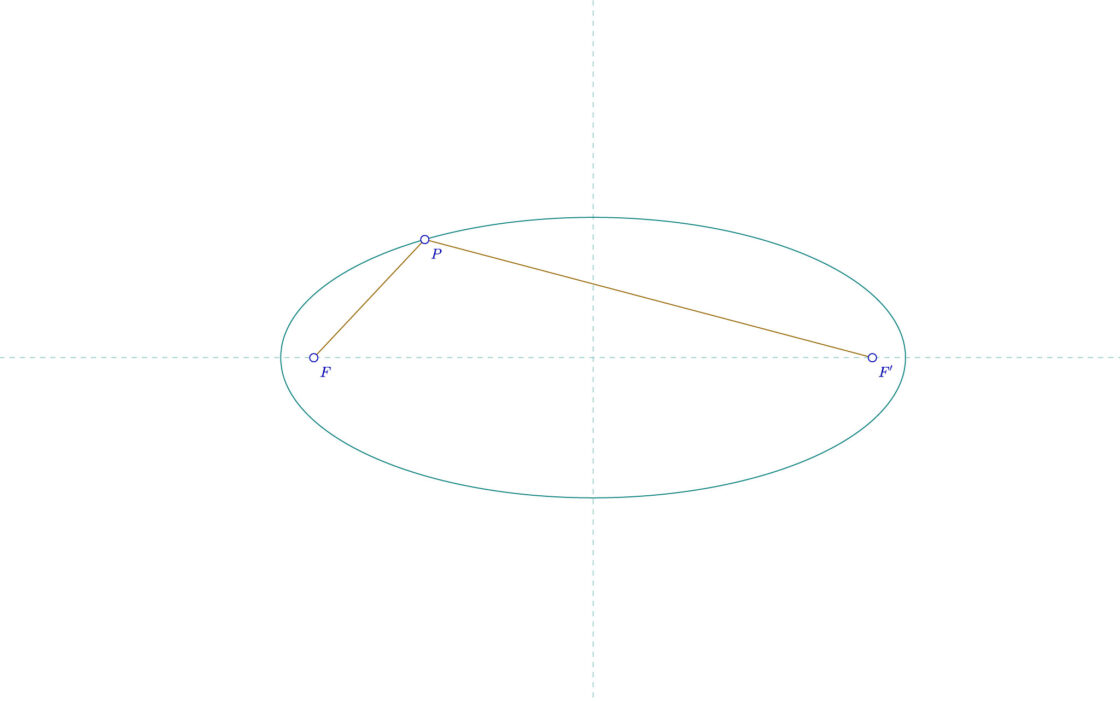
Las rectas que unen cualquier punto P sobre la curva de la elipse con los focos es lo que se conoce como radios vectores. Siempre se cumple la propiedad de que la suma de ambos radios vectores es igual a la longitud del eje mayor. La siguiente aplicación interactiva te permite comprobarlo moviendo los puntos A y B, que determinan los ejes. El punto P representa un punto cualquiera de la elipse.
Circunferencia principal
La circunferencia que tiene por centro el centro de la elipse y que además tiene como radio la mitad del eje mayor es lo que denominamos la circunferencia principal de la elipse.
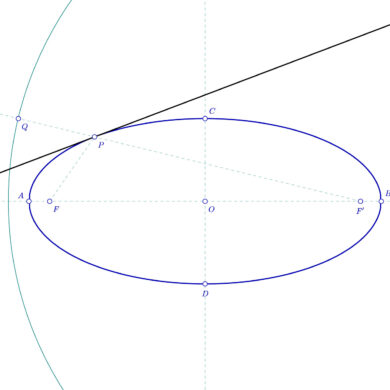
Técnicamente se define como el lugar geométrico de los pies de las perpendiculares trazadas por los focos a cada una de las tangentes.
Dicho así, a lo mejor la definición os resulta algo complicada, de modo que voy a tratar de explicarlo de forma más fácil. Imaginad que trazamos una recta cualquiera que pasa por uno de los focos. Luego trazamos una recta tangente a la elipse que es perpendicular a esa recta. Esta tangente corta a la recta anterior en el punto P, y es tangente en el punto T.
Como se que es un concepto un poco difícil de entender, te he preparado una aplicación interactiva que creo que te lo aclarará un poco. Puedes mover los puntos A y B para determinar el tamaño y forma de la elipse. Si mueves el punto T, verás a lo que me refiero.
Si trazaramos todas las posibles rectas que pasan por uno de los focos y unieramos todos los posibles puntos de corte de sus respectivas tangentes perpendiculares, tendríamos la circunferencia principal.
Diámetro conjugado de la elipse
Vamos a empezar por el principio por si hay alguien que se ha perdido la clase de hoy… Un diámetro es una cuerda de la elipse que pasa por su centro. En la imagen corresponde al segmento marcado por los puntos P1 y P2. Sabido ésto, el diámetro conjugado de un diámetro cualquiera será el lugar geométrico que forman los puntos medios de todas las cuerdas paralelas a él.
El segmento que delimitan R1 y R2 sería una cuerda cualquiera paralela al diámetro formado por P1 y P2, y el punto M sería el punto medio de dicha cuerda. Como podéis observar, la cuerda que pasa por M y O sería el diámetro conjugado de P1 y P2.
En la aplicación que tienes aquí abajo puedes mover los puntos A y B para modificar la forma y tamaño de la elipse. También puedes mover los puntos P1 y R1 para verificar que son y como funcionan los diámetros conjugados.
Circunferencias focales de la elipse
Las circunferencias focales de la elipse son aquellas que tienen como centro uno de los focos, y como radio el eje mayor.
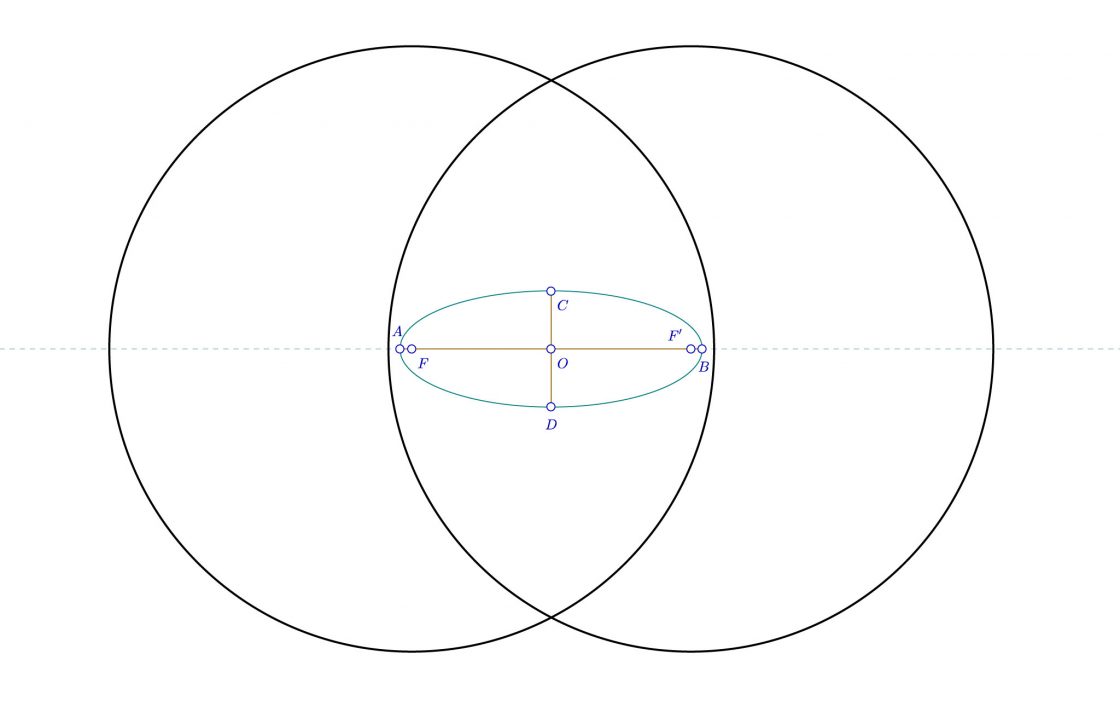
A éste respecto, la elipse también se puede definir como el lugar geométrico de los centros de las circunferencias que pasan por un foco y son tangentes a la circunferencia focal del otro foco.
Para que lo entendáis mejor, os pongo una imagen quitando una de las circunferencias focales para que se vea más claro.
Como podéis ver, el centro de la circunferencia sería el punto K y el punto J el punto de tangencia con la circunferencia focal. Por supuesto, en cualquier posición del punto K sobre la elipse se cumple que siempre pasa por F, que J es siempre tangente a la circunferencia focal y que la recta que une J y K pasa por F’
El concepto de circunferencia focal es realmente importante, ya que para hallar las tangentes a las curvas cónicas siempre vamos a recurrir a la circunferencia focal.
Problemas típicos con elipses
Construcción de una elipse conocidos sus ejes
Vamos a ver algunos de los problemas más comunes que nos podemos encontrar a la hora de trabajar con elipses. En éste caso se nos pide construirla, pero solo se nos proporciona la longitud de sus ejes. Nuestro punto de partida será algo similar a ésto:

- En primer lugar, con centro en uno de los extremos del eje mejor y radio igual a la mitad del eje mayor trazamos un arco de circunferencia que corta al eje mayor en los puntos F y F’, que son los focos de la circunferencia.
- Como sabemos que la suma de la distancia de los dos ejes a cualquier punto de la elipse es siempre igual a su eje mayor, realizamos tres marcas en una de las mitades del eje mayor, a las que vamos a llamar E, H e I, no tienen porqué ser equidistantes, y las podemos situar en cualquier punto sobre el eje mayor.
- Vamos a empezar con el punto E. Con radio igual al segmento AE trazamos dos arcos, uno desde el punto F y otro desde el punto F’
- Ahora con radio igual al segmento CE trazamos otros dos arcos, desde F y F’. Donde cortan a los arcos que trazamos en el paso anterior (por arriba y por abajo) tendremos cuatro puntos que pertenecen a la elipse. A éstos puntos los he llamado E1, E2, E3 y E4, para hacer referencia al punto que usamos para medir.
- Repetimos el proceso y con los puntos H e I, y de ese modo obtendremos otros cuatro pares de puntos que forman parte de la elipse. Llegados aquí solo tenemos que unir los puntos y tendremos la solución al problema.
Aquí abajo tienes un vídeo explicativo donde puedes ver como se resuelve paso a paso.
Otros problemas relacionados con éste serían:
Construir una elipse conociendo los focos y un punto de la misma
Recuerda que la suma de los radios vectores (distancia de los focos al punto) es igual al tamaño del eje mayor. En este caso, tu punto de partida será semejante a ésto.


Se resuelve de la siguiente manera:
- Dibuja la línea que pasa por F y F’ a esta recta la llamaremos r.
- Halla la mediatriz de F y F’. Al punto donde la mediatriz corta a la línea que dibujaste antes, llámalo O. Ese punto es el centro de la elipse.
- Toma la medida de F a P con el compás y dibuja hasta cortar la recta r, el punto donde corta lo llamaremos Q.
- Ahora toma la medida de F’ a P. Con esa misma medida, con centro en Q y a continuación del mismo, dibuja un arco que corte a la recta r en el punto R. El segmento que forman F y R es el tamaño del eje mayor.
- Traza la mediatriz del segmento que forman F y R. De esa manera obtienes el punto S.
- Mide la distancia entre F y S con el compás, y con esa misma medida, y centro en O, traza un arco que corta a la recta r en los puntos A y B, que delimitan el eje mayor de la elipse.
- Sin cambiar la medida que tienes en el compás, con centro en F (o F’) traza un arco que corta a la mediatriz de F y F’ en los puntos C y D. Esos puntos son los vértices del eje menor.
- Ahora ya puedes dibujar la elipse igual que hiciste en el ejercicio anterior.
Dibujar la elipse conociendo el eje mayor y los focos
Este caso es más sencillo que el anterior. Tu punto de partida será algo parecido a ésto.
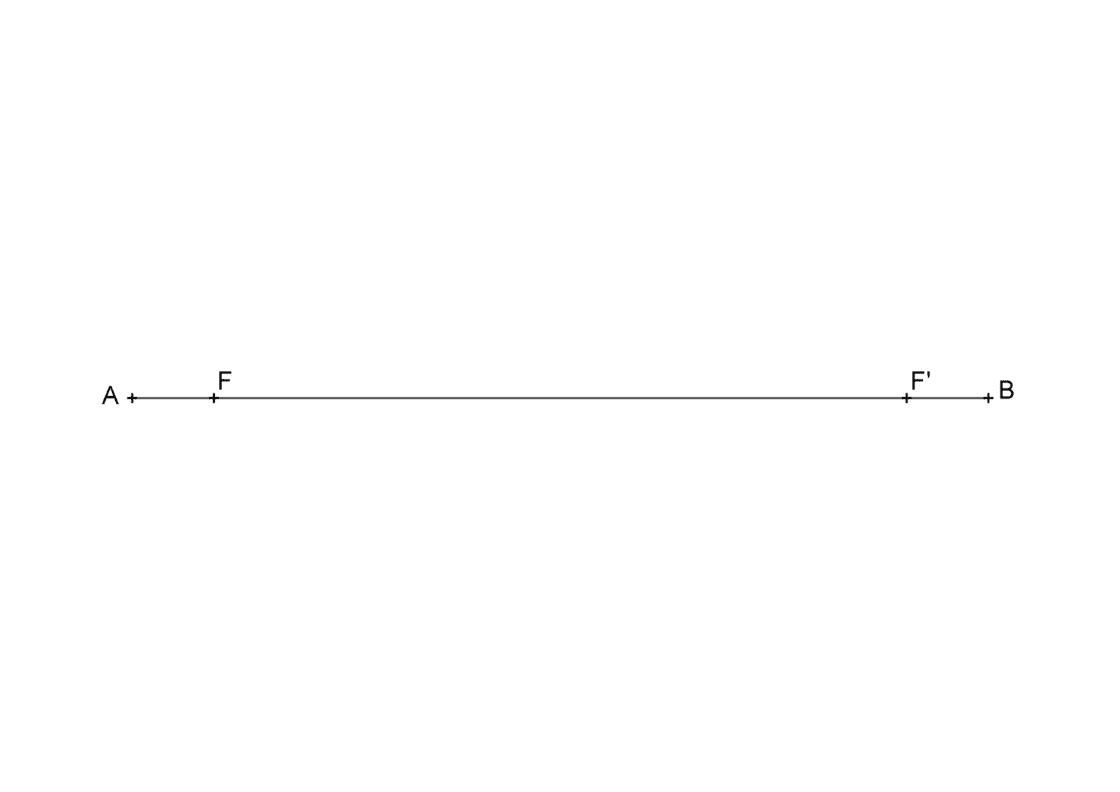

- Traza la mediatriz del eje mayor (segmento AB)
- Donde la mediatriz corta al eje mayor tienes el punto O.
- Usando el compás, mide la distancia entre O y A.
- Con esa misma distancia, y centro en el foco F, dibuja un arco que corta a la mediatriz que dibujaste antes en los puntos C y D.
- Los punntos C y D determinan el eje mejor. A partir de aquí, lo resuelves como en el vídeo de más arriba.
Dibujar la elipse conociendo el eje menor y los focos
Los datos que dispones son el eje menor CD y los Focos F y F’. Tu punto de partida será parecido a éste:
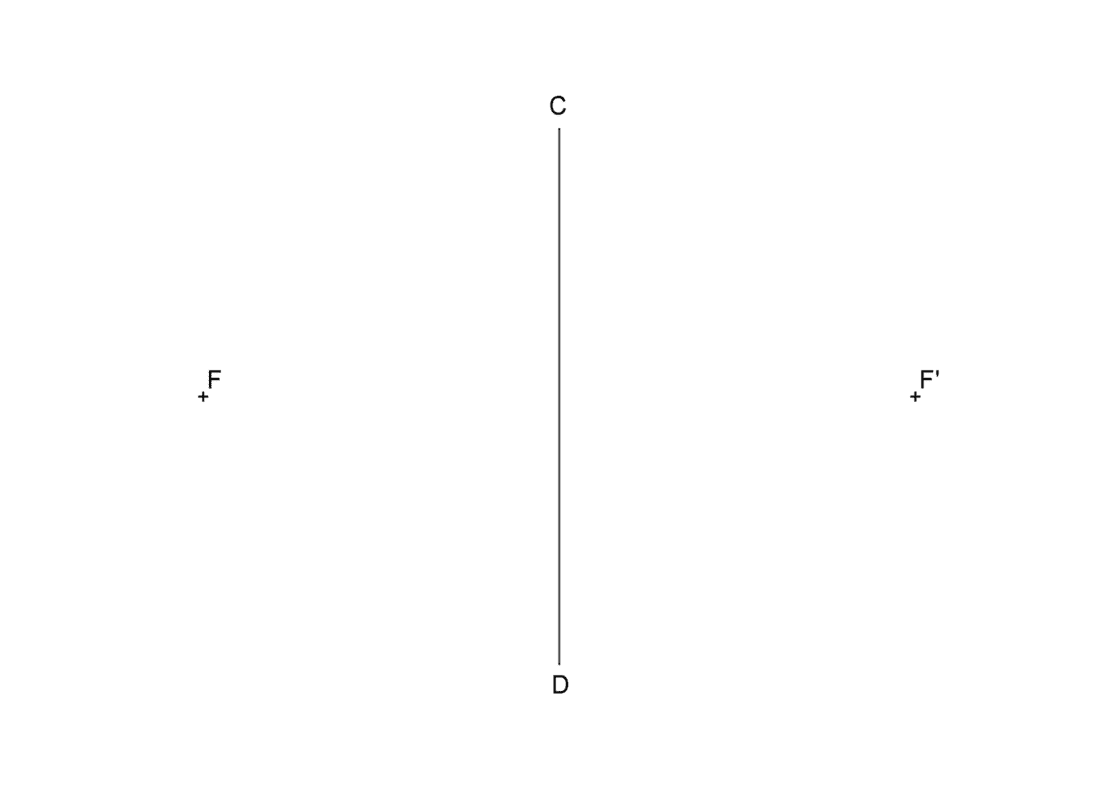
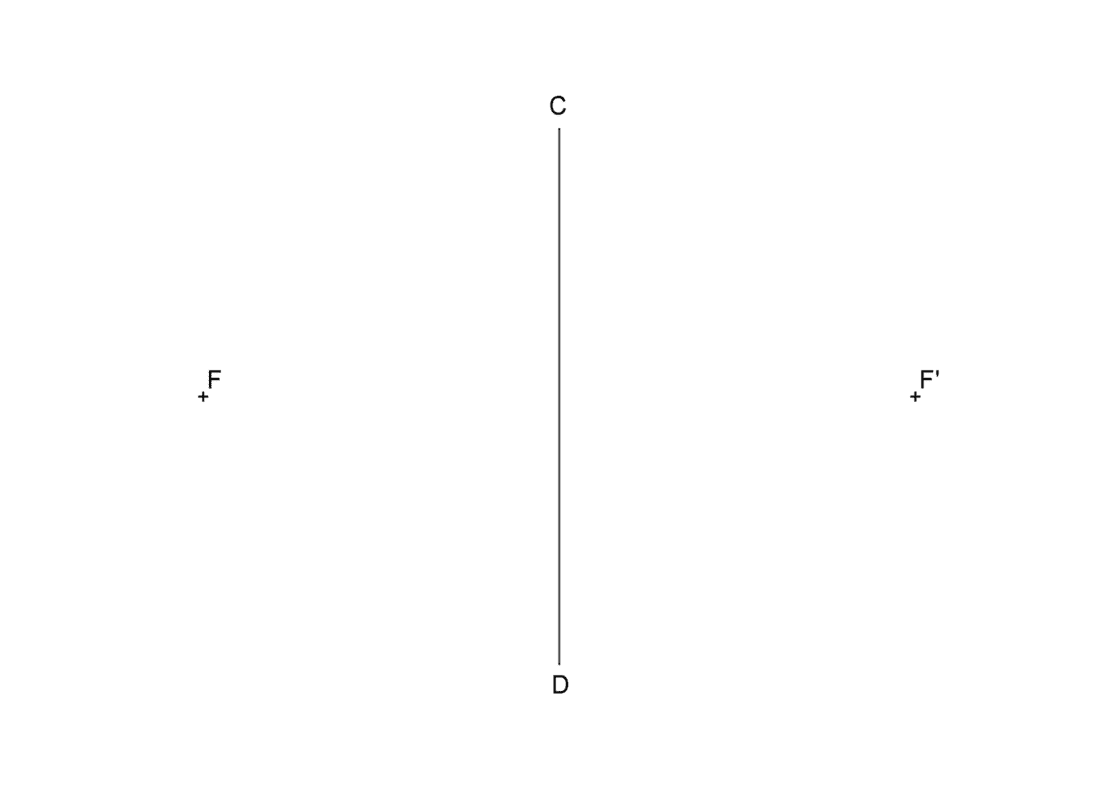
- Prolonga la línea que une a F con F’. A esta recta la llamaremos r.
- Donde esa recta corta al eje menor tienes O.
- Usando el compás, mide la distancia de F a C.
- Con esa misma distancia y centro en O, dibuja un arco que cortará en A y B. Estos puntos determinan el eje mayor. A partir de aquí, puedes resolver el ejercicio como te explico un poco más arriba.
Trazado de la elipse mediante haces proyectivos
En éste tipo de ejercicios se nos proporciona, al igual que en el anterior, la longitud de los dos ejes. Pero en ésta ocasión lo vamos a solucionar utilizando la escuadra y el cartabón en vez de el compás. Tu punto de partida debería parecerse a ésto:



- Dibujamos el rectángulo que contiene a la elipse.
- Dividimos los ejes en el mismo número de partes utilizando el teorema de Tales, en éste ejemplo lo he dividido en cinco partes. Los puntos intermedios los he llamado 1, 2 y 3 en el eje mayor y 1′, 2′ y 3′ en el lado paralelo al eje menor.
- Trazamos rectas que unen el punto C con cada uno de los puntos en la paralela al eje menor.
- Desde el punto D (opuesto en el eje menor) trazamos rectas que pasan por cada uno de los puntos marcados en el eje mayor.
- En el punto donde se cortan la recta que parte de C hasta 1′ y la recta que parte de D y pasa por 1 tenemos el punto P que pertenece a la elipse. En el punto de corte de la recta que pasa por C y 2′ con la recta que pasa por D y 2 tendremos el punto R. Por último, en el corte de la recta que pasa por C y 3′ con la recta que para por D y 3 tendremos el punto S.
- Repitiendo el proceso en los otros tres cuadrantes tendremos puntos suficientes para dibujar la solución solicitada.
Método de las circunferencias
En ésta ocasión vamos a dibujar la elipse utilizando para ello el método basado en las circunferencias principal y la del diámetro. Al igual que en ejercicios anteriores, lo que conoces son los dos ejes, determinados por los segmentos AB y CD. Tu punto de partida debería parecerse a ésto:
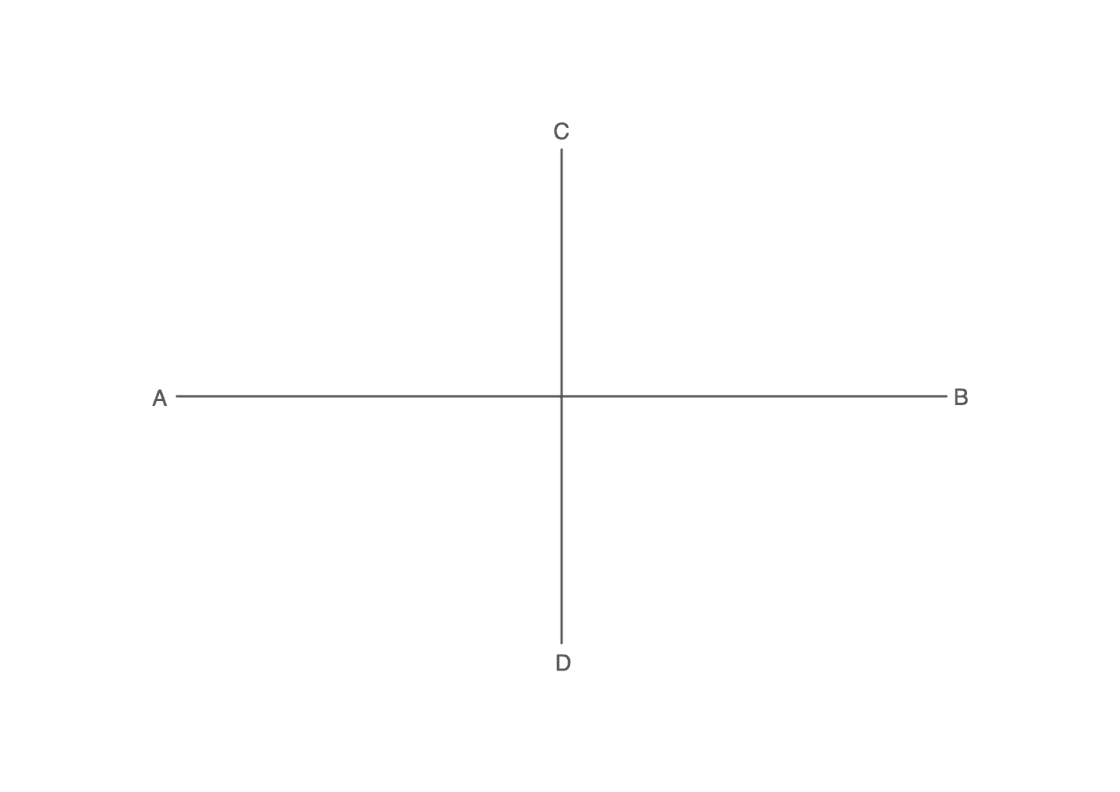

- Dibujamos la circunferencia principal y la circunferencia de diámetro.
- Trazamos una recta cualquiera que corta a ambas circunferencias en los puntos R y S, y en sus simétricos R’ y S’
- Dibujamos un par de rectas paralelas al eje mayor que pasan por R y R’
- Hacemos otro par de rectas perpendiculares al eje mayor y que pasan por S y S’
- En el punto en que se cortan dichas rectas, tenemos los puntos P y P’ que pertenecen a la elipse.
- Solo tenemos que repetir el proceso unas cuantas veces para hallar más puntos, a fin de que el resultado se más preciso.
- Para terminar solo tenemos que unir dichos puntos para hallar la solución.
Trazado a partir de envolventes
Sinceramente, éste es un método que a mi personalmente no me gusta nada. Lo menciono aquí solo a título informativo, ya que considero que no es un método nada preciso, y que además requiere bastante trabajo. Eso sí, para trabajos creativos o artísticos puede llegar a ser muy interesante.
Básicamente consiste en dibujar la circunferencia principal. Acto seguido trazamos rectas que pasan por los focos y que cortan a dicha circunferencia. Por último realizamos perpendiculares a esas rectas que pasan por los puntos de corte.
Trazado a partir de un par de diámetros conjugados
En ésta ocasión vamos a trabajar también con haces proyectantes, pero a diferencia del anterior ejercicio, ahora serán oblicuos. Tu punto de partida serán un par de ejes conjugados, algo parecido a lo siguiente:
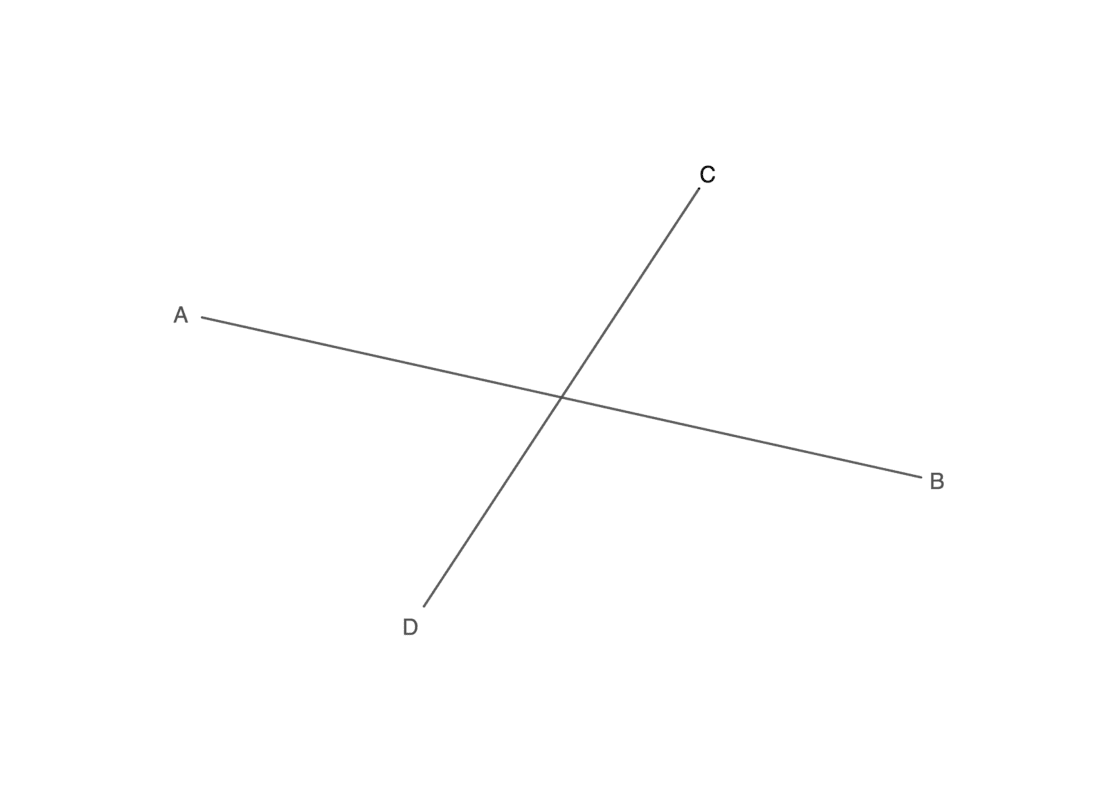


- A los extremos de los ejes los vamos a llamar A, B, C y D para mayor comodidad, siendo A y B los extremos del eje mayor y C y D los del eje menor.
- Dibujamos paralelas por cada uno de los puntos, delimitando así un romboide que contendrá a la elipse que buscamos.
- Usando el teorema de Tales dividimos en un número de partes iguales las paralelas al eje menor y el eje mayor. A esos puntos los he llamado 1, 2 y 3 en el eje mayor y 1′, 2′ y 3′ en la paralela al eje menor.
- A partir de éste punto procedemos como en el ejercicio anterior, hallando las intersecciones de C1′ con D1, C2′ con D2 y así sucesivamente, repitiendo el proceso en los cuatro cuadrantes.
- Uniendo esas intersecciones obtenemos la elipse buscada.
Método de los triángulos semejantes
Aparte del procedimiento mediante haces proyectivos, hay otra manera de hallar la elipse mediante una circunferencia y triángulos semejantes. El punto de partida es el mismo que en el ejercicio anterior, parecido a lo siguiente:



- En primer lugar trazaremos una circunferencia cuyo diámetro sea el mayor de los dos diámetros conjugados, en ésta caso el diámetro que determinan A y B.
- Trazamos una perpendicular a dicho diámetro que pasa por O. Este diámetro corta a la circunferencia en los puntos E y F.
- Para hallar la solución ahora tenemos que trazar triángulos semejantes al que forman los puntos OCE y ODF.
- Si no recuerdas como hacer triángulos semejantes, debes hacer paralelas al segmento EF, y por los puntos de corte con la circunferencia y con el diámetro AB trazas paralelas a los segmentos EC, DF y al diámetro menor CD.
Aquí abajo puedes mover el punto azul para ver como los triángulos semejantes se corresponden.
En ésta imagen he sombreado los dos triángulos que sirven de referencia, para ayudaros a comprender el concepto.
Como hallar los ejes de una elipse
Supongamos que tienes una elipse, pero no conoces ni el centro, ni los ejes, y mucho menos los focos. ¿Puedes hallar esos elementos? La respuesta es «si». Para ello vas a aplicar dos conceptos que tienes explicados más arriba. El primero se trata de la simetría de la elipse (es fundamental para resolver este problema). El segundo hace referencia a los ejes conjugados. Tu punto de partida debe parecerse a ésto:

- En primer lugar, dibuja una cuerda cualquiera de la elipse. Puedes llamarla P y P’.
- Luego dibuja otra cuerda de la elipse, pero es importante que sea paralela a la primera. La llamaremos R y R’.
- Dibuja mediatrices de ambas cuerdas para hallar sus puntos medios y une esos puntos medios con una línea.
- Esa línea que acabas de dibujar y que corta a la elipse es un diámetro de la elipse. Sabiendo esto, sabemos que su punto medio coincide con el centro de la elipse.
- Traza pues la mediatriz de ese diámetro, y así obtienes O, el centro de la elipse.
- Como sabemos que O es el centro, y que la elipse es simétrica respecto de los dos ejes, si dibujamos cualquier arco con centro en O y que corte a la elipse en cuatro puntos, haciendo las mediatrices de esos puntos tendrás los ejes. Para este ejemplo he utilizando una circunferencia de centro O y radio hasta P. Esa circunferencia corta en M, N y Q.
- Realiza las mediatrices de P y M por un lado, y de P y N por el otro. Esas mediatrices te determinan los ejes de la elipse.
- Para hallar los focos, puedes utilizar el método habitual una vez conocidos los ejes.
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti. Gracias de antemano por dejar tu comentario un poco más abajo.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
Entradas relacionadas
22 enero, 2021
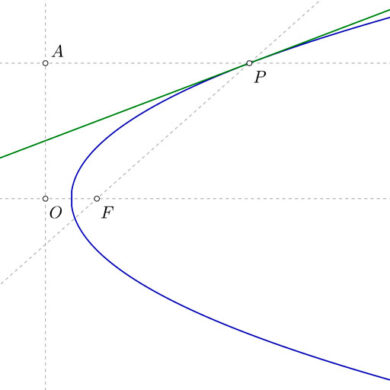

Recta tangente a la parábola
19 enero, 2020
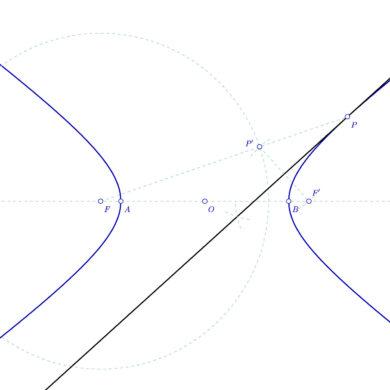

Tangente a la hipérbola
18 enero, 2020