Tangencias. Propiedades de la tangente y puntos de tangencia

En Geometría y en su aplicación a través del dibujo técnico, nos podemos encontrar con multitud de aplicaciones de tangencias o de enlace de líneas que pueden presentar un grado de mayor o menor complejidad. En ésta ocasión, me quiero centrar en especial sobre aquellos tipos de problemas de rectas y circunferencias tangentes que presentan algún tipo de aplicación práctica a la hora de resolver problemas que implican formas geométricas. El resto de problemas tienen un interés sobretodo geométrico y de resolución de problemas más complejos.

Propiedades de las tangencias

Se puede decir que una recta y una circunferencia, o dos circunferencias, son tangentes cuando solo tienen en común un único punto. Así pues, podemos afirmar que las tangencias o enlaces de líneas se basan en las siguientes propiedades:

Cuando dos circunferencias son tangentes entre si, el punto de tangencia se encuentra en la línea que une los centros de ambas.
En el caso de que una recta sea tangente a una circunferencia, el punto de tangencia correspondería al pie de la perpendicular trazada desde el centro de la circunferencia a dicha recta.
Si una circunferencia es tangente a dos rectas que se cortan, entonces el centro de la circunferencia se encuentra en la bisectriz del ángulo que forman dichas rectas.
En cualquier cuerda de circunferencia, su mediatriz pasa por el centro de la circunferencia, de modo que divide en dos partes iguales no solo la propia cuerda, sino la circunferencia y el arco que define.

Para resolver problemas de tangencias debemos tener muy en cuenta los datos que se nos proporcionan y lo que se nos solicita. En todo momento debemos ser capaces de razonar las construcciones que realicemos paso a paso, explicando el «porqué» de nuestras acciones. Debemos tener en cuenta que en más de una ocasión nos encontraremos con determinados problemas que nos brindan la posibilidad de encontrar más de una respuesta válida.

Trazado de rectas tangentes

Recta tangente a una circunferencia que pasa por un punto de la misma

Ante éste problema se nos pueden plantear dos situaciones diferentes. En el primero de ellos conocemos el centro de la circunferencia. Esta es la situación más común a la que nos podemos enfrentar. En la segunda la circunferencia es tan grande que el centro de la misma está fuera de la hoja, por lo que trabajamos solo con un arco. Este segundo caso te explicaré más abajo como resolverlo. Para este primer caso el punto de partida será este:

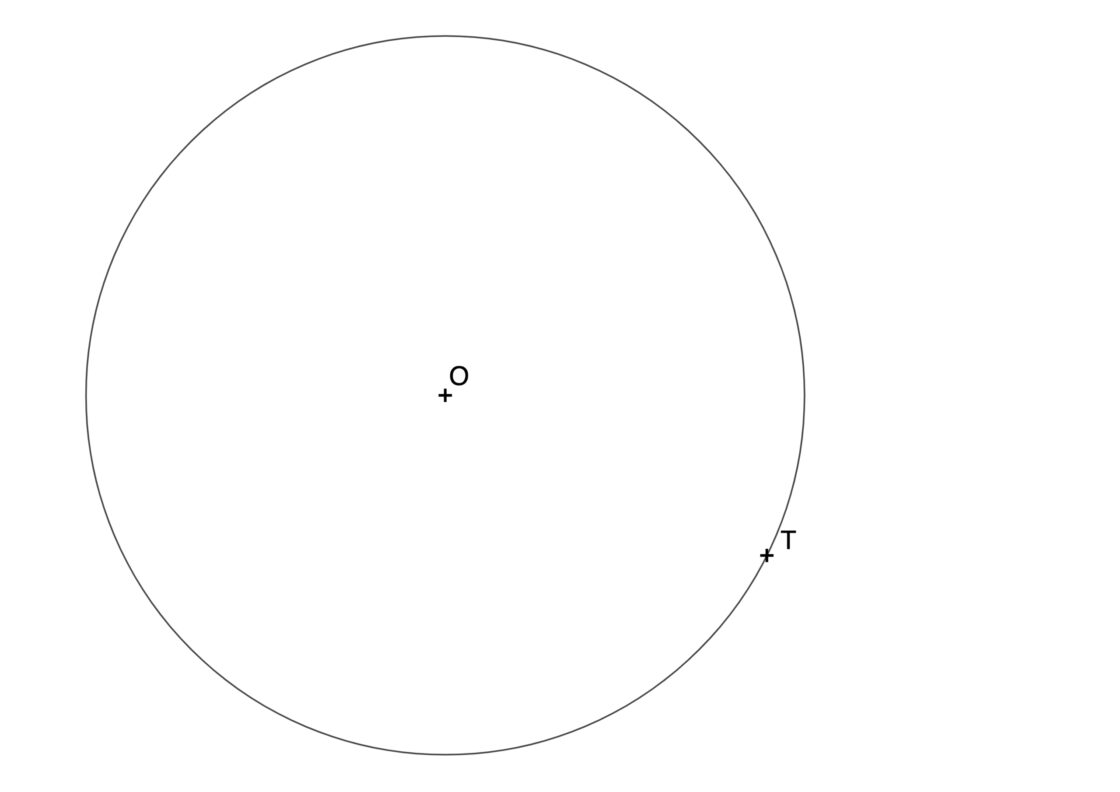
En primer lugar, unimos el centro de la circunferencia con el punto de tangencia T. Éste segmento lo vamos a prolongar un poco más porque luego lo necesitaremos.
Ahora debemos hallar la recta perpendicular al segmento O₁T.
Esa recta perpendicular será la tangente que estamos buscando.

Aquí abajo tienes un vídeo con todo el proceso, por si todavía tienes dudas de como se realiza.

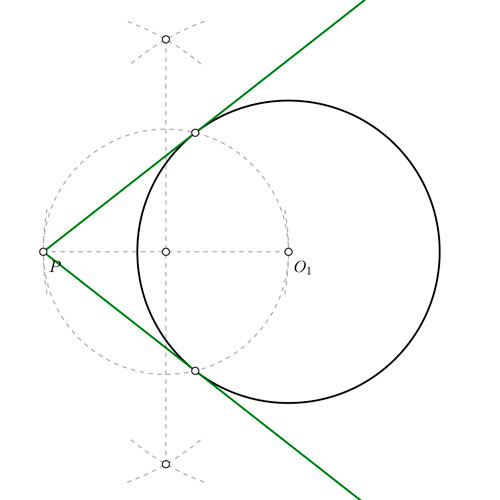
Rectas tangentes a una circunferencia por un punto exterior de la misma

Sin duda alguna, éste es el problema más recurrente en el tema de tangencias. Créeme cuando te digo que éste problema se te debe grabar a fuego. Si no te aprendes bien éste ejercicio, serás totalmente incapaz de realizar casi ninguno de los que siguen, o de niveles más avanzados, como de segundo de bachillerato. Tu punto de partida será algo parecido a esto:

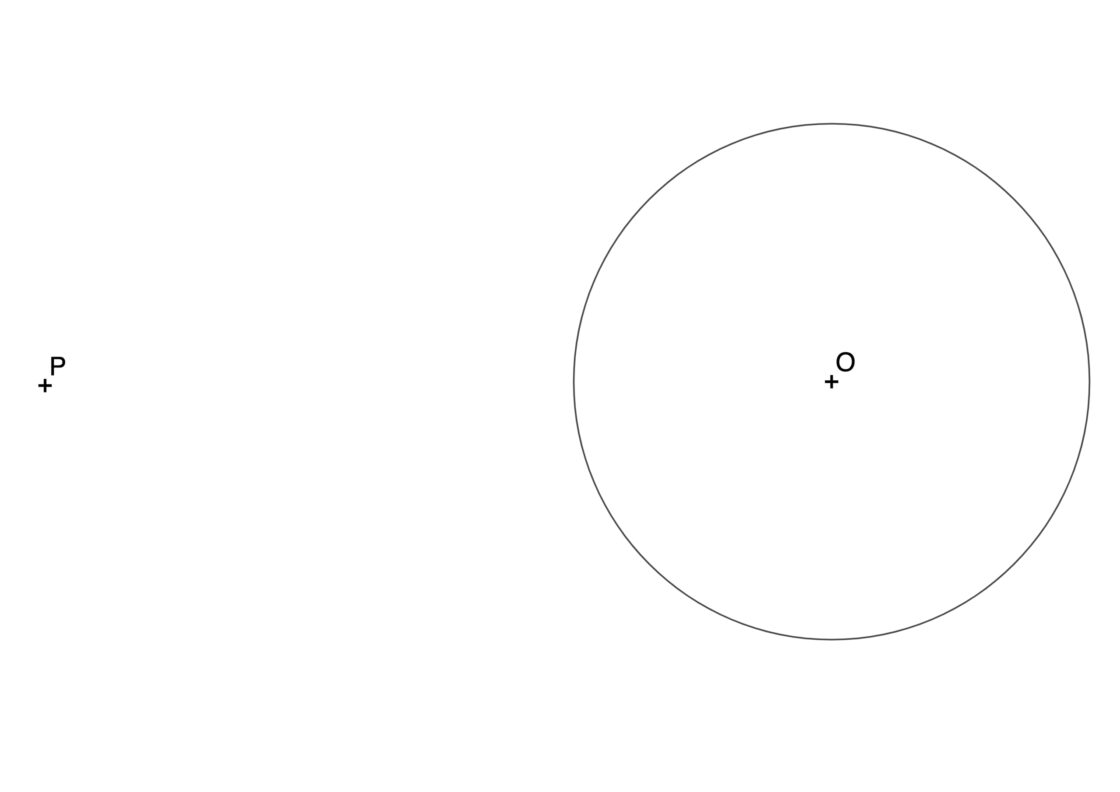
Primero debes dibujar la recta que une el punto P con el centro de la circunferencia.
¿Te acuerdas del concepto de mediatriz? Pues debes dibujar una mediatriz para hallar el punto medio de ese segmento que acabas de dibujar.
Con centro en ese punto medio, y radio hasta P, tienes que trazar un arco que cortará a la circuferencia inicial en los puntos T₁ y T₂
Para finalizar, une P con los puntos T₁ y T₂ y verás que esas son las rectas que estás buscando.

Si todavía tienes dudas acerca de dibujar este tipo de tangentes, aquí abajo tienes un vídeo donde te explico como se hace todo el proceso.

Recta tangente a un arco por un punto del mismo

En éste caso se nos pide hallar la recta tangente a un arco de circunferencia cuando conocemos el punto de tangencia T sobre el mismo. El problema en éste tipo de situaciones es que la circunferencia es tan grande que el centro de la misma se encuentra fuera del plano. Por ese motivo debemos proceder de otra manera. Tu punto de inicio será algo parecido a este:

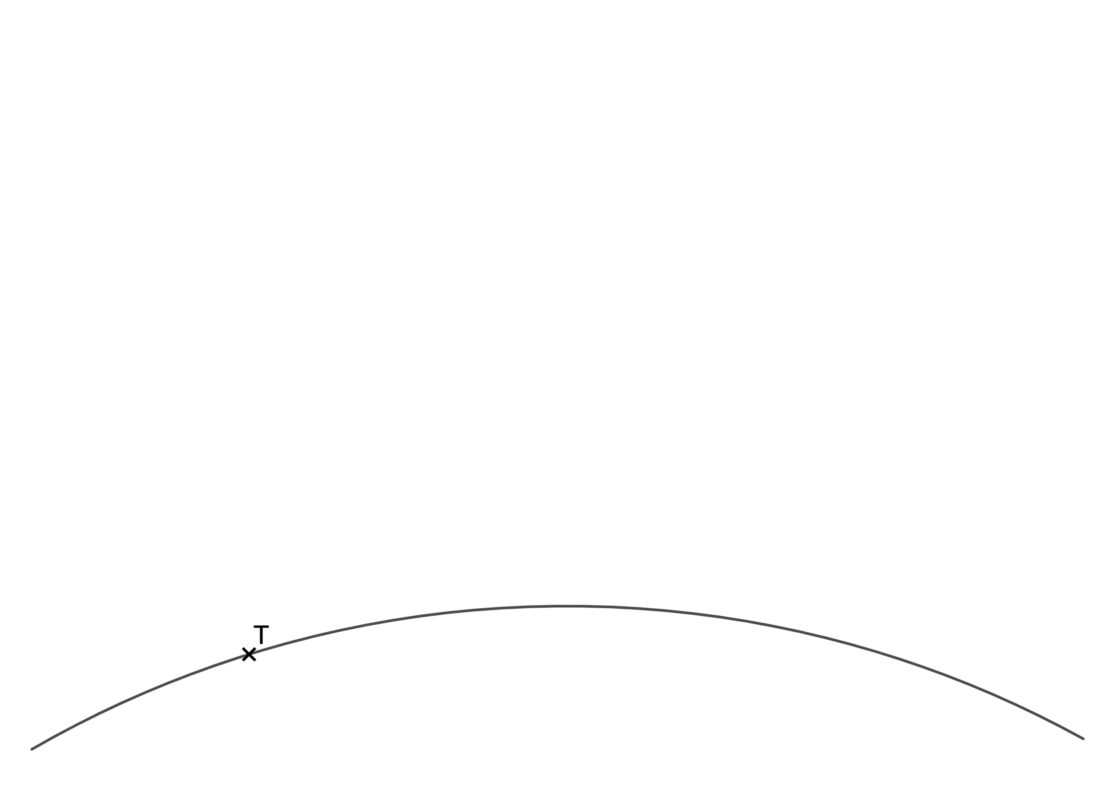
Para empezar, desde el punto de tangencia T, con un radio cualquiera, trazamos un arco que cortará al arco conocido en un punto. A éste punto lo vamos a llamar R.
Con centro desde R y exactamente el mismo radio, trazamos otro arco que cortará en el punto S al arco inicial.
Trazamos un arco con centro en T y radio TS. Donde ese arco corta al que tiene centro en R y radio RS, tenemos un punto que se encuentra sobre la recta tangente.
Uniendo el punto recién obtenido y T, estaremos dibujando la recta tangente al arco que pasa por el punto T.

Aquí abajo tienes todo el proceso en un vídeo, por si todavía tienes alguna duda.

Rectas tangentes a una circunferencia y paralelas a una recta dada

En ésta ocasión se nos pide hallar las dos rectas tangentes a una circunferencia dada de centro O₁ y que además son paralelas a una recta r que conocemos. Tu punto de partida se va a parecer a algo como esto:

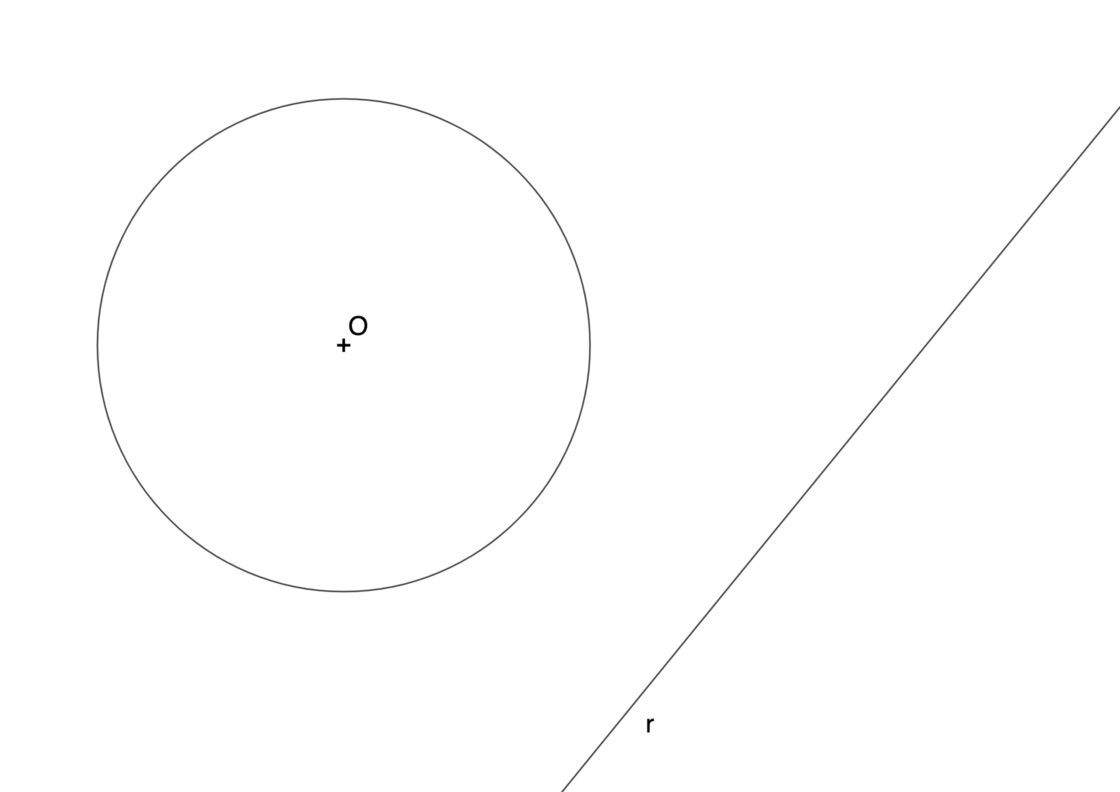
Lo primero que tienes que hacer es dibujar una recta perpendicular a la recta conocida r, pero que pase por el centro de la circunferencia.
Los puntos donde esa recta perpendicular corta a la circunferencia nos determinan los puntos de tangencia T₁ y T₂
Si trazamos paralelas a la recta original r, por los puntos T₁ y T₂ tendremos las dos rectas tangentes que estamos buscando.

Aquí abajo tienes una aplicación interactiva para comprobarlo. Puedes mover los puntos P y R para verificar la construcción.

Aquí abajo te dejo un vídeo explicativo para que veas el proceso completo en caso de que todavía tengas alguna duda.

Rectas tangentes exteriores a dos circunferencias

Este es otro problema muy típico de problemas de tangencias de primero de bachillerato. Conocemos dos circunferencias y se nos pide hallar las rectas tangentes exteriores a ambas. Tu punto de partida se parece a esto:

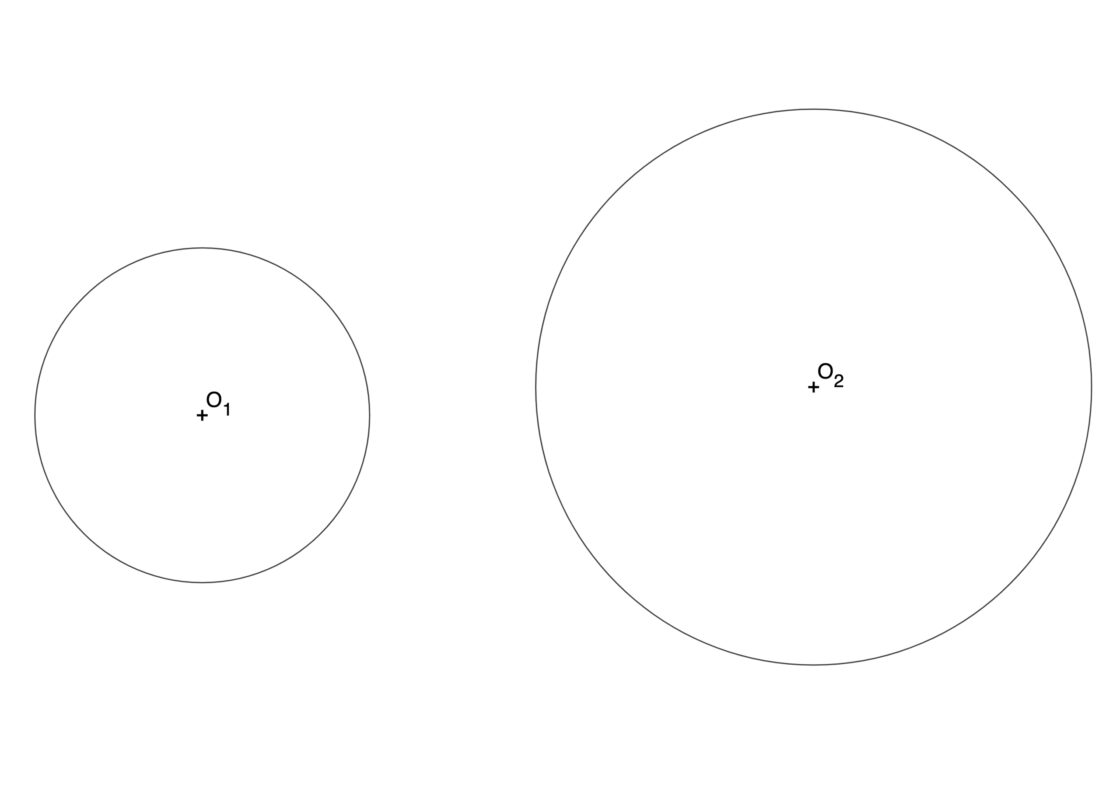
Empieza trazando la línea que une los centros de las dos circunferencias. El punto donde esa recta corta a la circunferencia de radio mayor, llámalo A.
Ahora mide con el compás el radio de la circunferencia menor, representado en este caso por el segmento O₁P y lleva esa misma medida desde el punto A, hallando el punto B. Como aclaración, la circunferencia de radio O₂B es la resta de ambas circunferencias.
A continuación tienes que hallar los puntos de tangencia del centro O₁ con la circunferencia de centro O₂ y radio O₂B
Para ello, traza la mediatríz del segmento que forman O₁ y O₂ para hallar el punto medio C
Con centro en C y radio hasta O₂ traza un arco que corta a la circunferencia de centro O₂ y radio hasta B. Los puntos de corte son T₁ y T₂
Dibuja líneas que pasen por T₁ y T₂ y prolóngalas hasta cortar a la circunferencia mayor. Los puntos de corte son T₃ y T₄
Si ahora trazas perpendiculares a los radios que forman O₂ y T₃ por un lado y O₂ y T₄ por el otro, tendrás las rectas tangentes que buscas.

Como este ejercicio es un poco más complejo que los anteriores, te recomiendo que veas el siguiente vídeo en caso de que aun tengas dudas.

Rectas tangentes interiores a dos circunferencias

Este ejercicio es similar, solo que en ésta ocasión lo que te piden son las rectas tangentes interiores. Es decir, las que pasan entre las dos circunferencias. Tu punto de partida será similar al anterior, en este caso es parecido a esto:

Empieza por trazar una recta que una los centros de las dos circunferencias. Los puntos de corte con las circunferencias serán P para la pequeña y A para la grande
Mide con el compás el radio de la circunferencia pequeña, determinado por el segmento que forman O₁ y P
Con esa medida, dibuja un arco que corte a la línea que une O₁ y O₂ en el punto B. Como aclaración, la circunferencia de radio O₂B es la suma de ambas circunferencias.
Dibuja pues a circunferencia de radio O₂B
Halla los puntos de tangencia del centro O₁ con la circunferencia que acabas de dibujar. Para ello halla el punto medio de ambos centros, que llamaremos C. Con centro en C y radio O₂C dibuja un arco que corte a la circunferencia de radio O₂B. Los puntos de corte son T₁ y T₂
Ahora dibuja líneas que unan T₁ y T₂ con el centro O₂. Los puntos donde esas líneas cortan a la circunferencia grande son T₃ y T₄
Para terminar, si trazas perpendiculares a esas líneas por los puntos T₃ y T₄ tienes las rectas tangentes interiores a las dos circunferencias.

Aquí abajo tienes un vídeo con todo el proceso. Te recomiendo que lo veas si todavía no tienes claro de como se realiza este ejercicio.

Tanto para este ejercicio, como para el anterior (o cualquier otro) si te piden hallar todos los puntos de tangencia, recuerda que solo tienes que hacer perpendiculares a las rectas tangentes que pasen por los centros de las circunferencias. Recuerda: Cualquier recta tangente a una circunferencia SIEMPRE es perpendicular al radio en el punto de tangencia.

Tangencias empleando homotecia

Los dos ejercicios anteriores se pueden resolver también empleando homotecia. La diferencia en ambos caso es si el centro de homotecia se encuentra entre las dos circunferencias o fuera de ellas. La manera de resolverlo es muy parecida en ambos casos. Veamos como se resuelve cada uno de ellos.

Como hallar las rectas tangentes exteriores a dos circunferencias empleando homotecia

Al igual que en los casos anteriores, tu punto de partida se parece a esto:

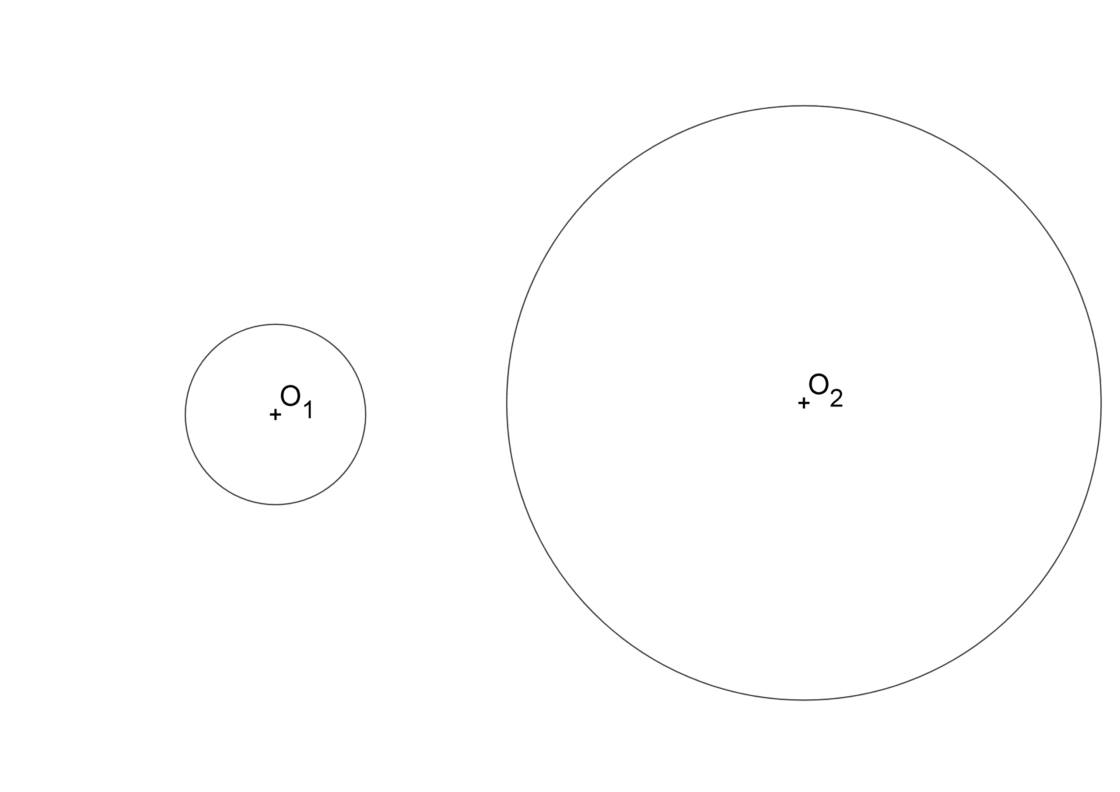
Comienza dibujando la recta que une los centros de las dos circunferencias. Sobre esa línea se encuentra el centro de homotecia.
Traza una recta cualquiera por una de las dos circunferencias. Si no te quieres liar, lo más sencillo es una perpendicular a la recta que dibujaste antes que pase por O₁ y de esa manera obtienes A.
Ahora realiza una recta paralela a la anterior que pase por O₂ y esa línea corta a la segunda circunferencia en B.
Marca la recta que une A y B hasta cortar a la línea que une O1 con O2 para hallar en su intersección O, el centro de homotecia.
Si hallas las rectas tangentes a las circunferencias que pasen por O, verás que son las mismas.

Rectas tangentes interiores a dos circunferencias empleando homotecia

Este ejercicio es similar al anterior, la diferencia principal es que A y B se trazan en direcciones opuestas, forzando que el centro de homotecia se encuentre entre ambas circunferencias. Así pues, tu punto de partida se parece a esto:

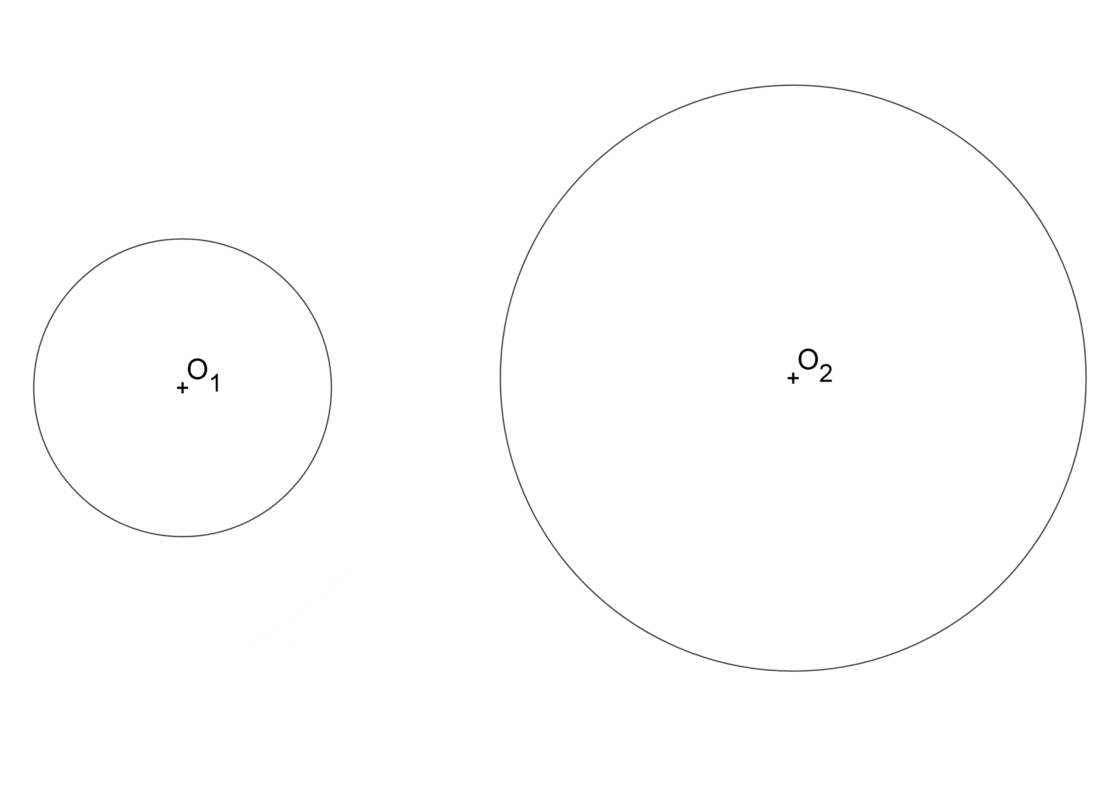
Comienza trazando la recta que une O₁ y O₂.
Realiza perpendiculares a esa línea que pasen por O₁ y O₂. La perpendicular que pasa por O₁ corta en la parte inferior de la circunferencia en A, y la que pasa por O₂ corta en la parte superior de la circunferencia en B.
Une A con B con una línea, donde esa línea corta a la que une O₁ con O₂ tienes el centro de homotecia O.
Halla las rectas tangentes a las circunferencias que pasan por O, esas son las rectas que estás buscando.