Sección plana de un cilindro con un plano proyectante vertical y su verdadera magnitud

Hallar la sección que produce un plano proyectante vertical con un cilindro de revolución es un ejercicio recurrente en el apartado de sistema diédrico en los exámenes de la EVAU. Pero este es un ejercicio mucho más sencillo de lo que puedes pensar. Para resolverlo te proporcionan las proyecciones diédricas del cilindro y el plano proyectante vertical, representado por sus trazas vertical y horizontal.

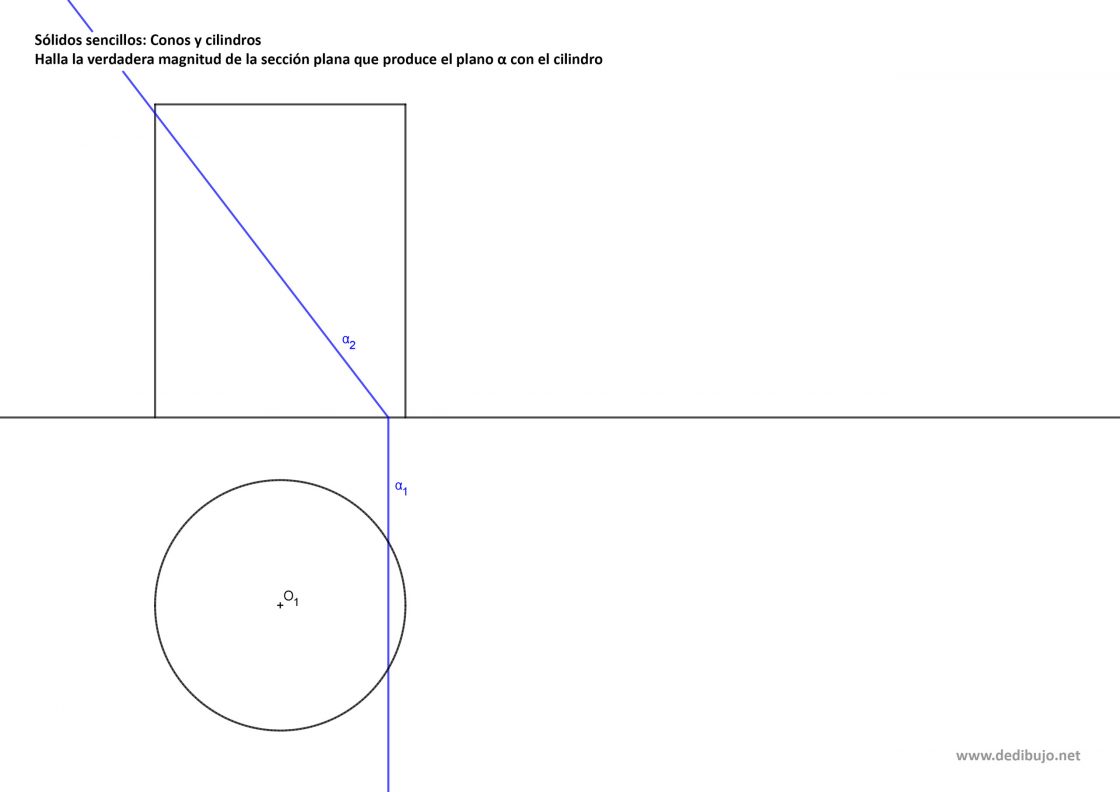
Tu punto de partida será algo parecido a ésto:

Como consejo personal, para entender este ejercicio te recomiendo que lo visualices cono como una superficie curva, sino como un prisma regular octogonal. Como verás a continuación se resuelve de la misma manera. En especial si no te piden dibujar la curva. Si ya has estudiado algo de perspectiva caballera, cónica o isométrica, el proceso recuerda vagamente a la construcción de círculos.

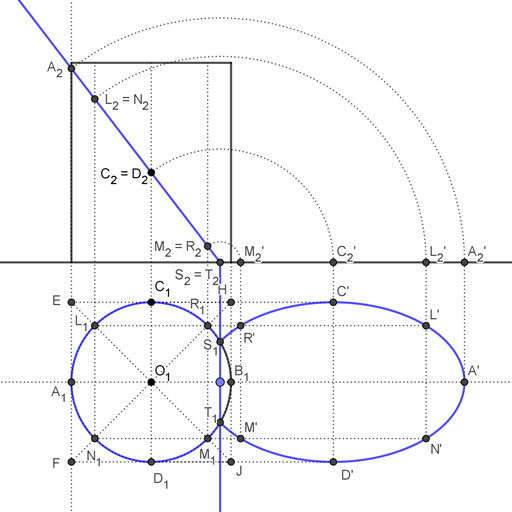
1. Empieza por dibujar una línea paralela a la línea de tierra y que pase por el centro de la base. De esa manera determinas los puntos A₁ y B₁. Prolóngala hacia la derecha, porque luego la necesitarás para hallar la verdadera magnitud de la sección.
2. Ahora traza una perpendicular a la línea de tierra que pase por el centro de la base. De esa manera no solo determinas los puntos C₁ y D₁. También determinas los puntos C₂ y D₂ (son el mismo punto) donde esa perpendicular corta a la traza vertical del plano.
3. Dibuja paralelas a la línea de tierra que pasen por C₁ y D₁. Prolóngalas hacia la derecha, ya que luego las vas a necesitar para hallar la verdadera magnitud de las sección. Por otra parte, dibuja perpendiculares a la línea de tierra que pasen por A₁ y B₁. Donde todas esas líneas se cortan tienes los puntos E, F, H y J, que determinan los vértices del cuadrado que contiene a la base.
4. Une E con J con una línea y F con H con otra. Esas líneas cortan a la circunferencia de la base en los puntos L₁, M₁, N₁ y R₁.
5. A continuación realiza perpendiculares a la línea de tierra que pasen por L₁ y R₁. Donde esas perpendiculares cortan a la traza vertical del plano tienes los puntos L₂ y N₂ (que son el mismo). Y por otra parte, M₂ y R₂ (que también coinciden).
6. Marca los puntos donde la traza horizontal del plano proyectante corta a la base. Esos puntos llámalos S₁ y T₁. Las proyecciones verticales de esos puntos se encuentran donde la traza corta a la línea de tierra. Son los puntos S₂ y T₂.
7. Continúa trazando paralelas a la línea de tierra que pasen por L₁ y N₁ y prolóngalas hacia la derecha. Ya has hallado la sección, ahora toca hallar su verdadera magnitud.
8. Con centro en S₂ haz arcos con radio hasta C₂, L₂, M₂ y A₂. Donde esos arcos cortan a la línea de tierra tienes los puntos C₂‘, L₂‘, M₂‘ y A₂‘. Ahora traza perpendiculares a la línea de tierra que pasen por esos puntos.
   1. Donde la perpendicular que pasa por A₂‘ corta a la paralela que pasa por A₁ tienes el punto A’.
   2. La perpendicular que parte de L₂‘ corta a las paralelas que pasan por L₁ y N₁ en los puntos L’ y N’ respectivamente.
   3. Los puntos donde la perpendicular que pasa por C₂‘ corta a las paralelas que pasan por C₁ y D₁ son C’ y D’.
   4. Por último, la perpendicular que pasa por M₂‘ corta a las paralelas que pasan por R₁ y M₁ en los puntos R’ y M’
9. Uniendo T₁, M’, D’, N’, A’, L’, C’, R’ y S₁ tienes la verdadera magnitud de la sección plana que produce el plano proyectante vertical con el cilindro de revolución.

Aquí abajo puedes mover el punto azul para ver las distintas posibilidades que te puedes encontrar, según si corta también a la base superior, o si no corta a ninguna de ellas.