En este caso se pide hallar la sección plana de un octaedro regular con un plano α paralelo a la línea de tierra. Este problema se puede resolver de dos maneras distintas; mediante un cambio de plano vertical, o mediante la tercera proyección. En el primer caso el nuevo plano vertical formará un ángulo de 90 grados con el plano vertical inicial. Desde mi punto de vista, la segunda opción es más sencilla, pues a estas alturas ya deberías ser capaz de dibujar la tercera proyección de una figura sin problemas.
Como hallar la sección plana de un octaedro causada por un plano paralelo a la línea de tierra
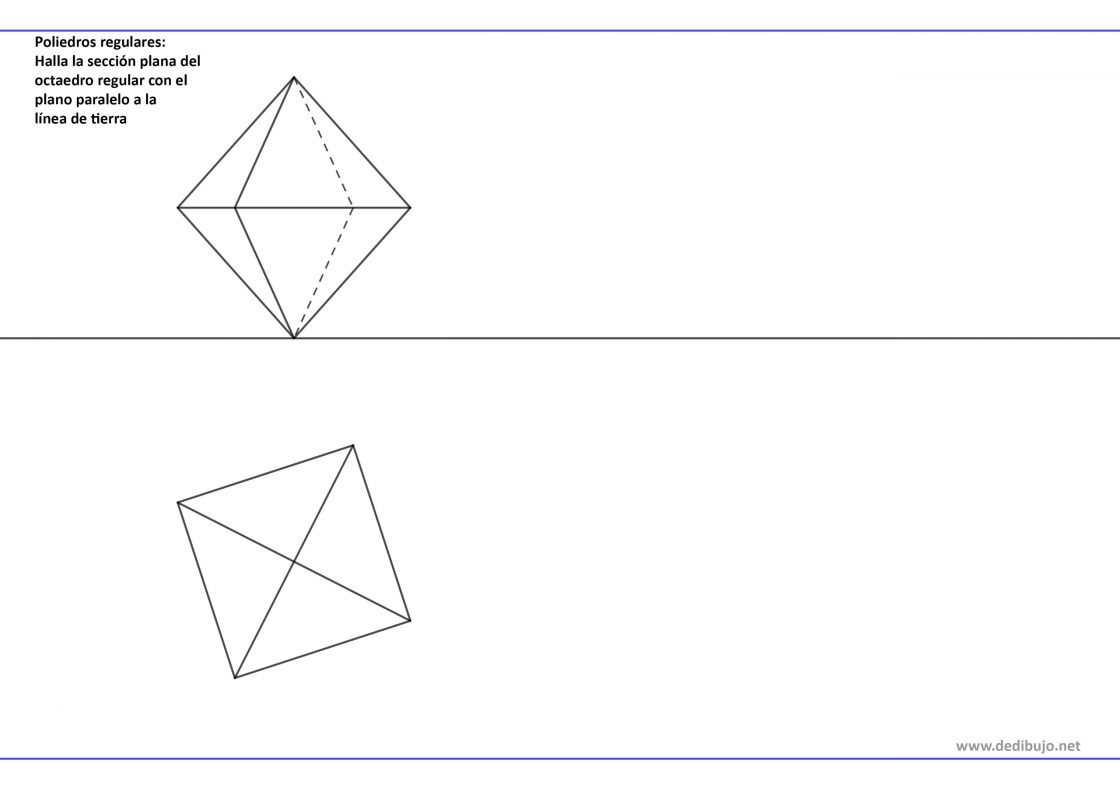
Lo más habitual es partir conociendo las proyecciones del octaedro. Esto es así más que nada para acortar el ejercicio, ya que puede ser bastante tedioso. No obstante, también se podría dar el caso de que te pidieran dibujar el octaedro y después hallar la sección. El plano α esta representado por sus trazas, que son dos líneas paralelas a la línea de tierra. Aquí abajo las puedes ver como las dos líneas azules.
Tu punto de partida será algo parecido a esto:
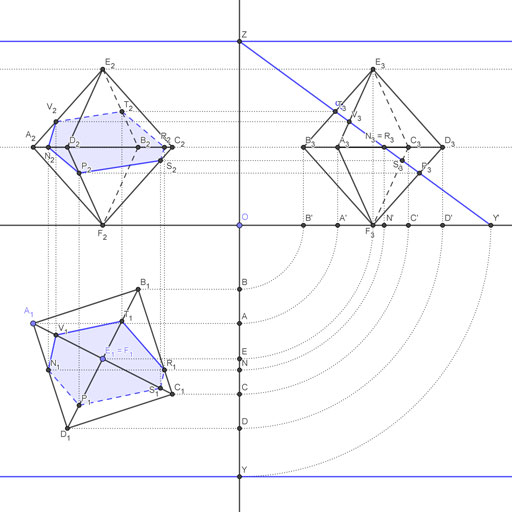
Resolver este ejercicio directamente es bastante complicado, por no decir imposible. Por ello para poder resolverlo vamos a recurrir a la tercera proyección. De esta manera el plano se transforma en un plano proyectante y podrás hallar los puntos de intersección de forma mucho más sencilla. Lo más complicado en este ejercicio es no confundir las líneas al trasladar el punto de intersección. Por eso te recomiendo que pongas nombre a todos los puntos para poder identificar las aristas. Aquí abajo a los puntos iniciales del octaedro los he llamado A, B, C, D, E y F, representados por sus proyecciones A1, A2, B1, B2… etc.
- Empieza dibujando una perpendicular a la línea de tierra por un punto cualquiera. A ese punto lo llamaremos O, ya que será el centro del triedro que representan las tres proyecciones. Los puntos de intersección de la perpendicular con las trazas del plano α llámalos Y sobre la traza horizontal y Z sobre la traza vertical.
- Traza paralelas a la línea de tierra que pasen por A1, B1, C1, D1 y E1 (que coincide con F1). Donde estas paralelas cortan a la perpendicular que dibujaste antes tienes A, B, C, D, E y F.
- Con centro en O y radio hasta A, B, C, D, E, F e Y, traza arcos que corten a la línea de tierra. De esa manera obtienes A’, B’, C’, D’, E’, F’ e Y’.
- Ahora dibuja paralelas a la línea de tierra que pasen por A2, B2, C2, D2 y E2. Dibuja también perpendiculares a la línea de tierra que pasen por A’, B’, C’, D’, E’, F’ e Y’. En la intersección de la paralela por A2 y la perpendicular por A’ tienes A3. Donde se cortan la paralela por B2 y la perpendicular por B’ tienes B3 y así sucesivamente.
- Une E3 con A3, E3 con B3, E3 con C3… y así sucesivamente para obtener la tercera proyección del octaedro. Como te decía es importante hacerlo bien para representarlo correctamente. Recuerda también representar las líneas ocultas como discontinuas, para ver la figura de forma más clara (y correcta).
- Lo siguiente será unir el punto Z con Y’ para obtener la traza sobre el plano de perfil del plano α (su tercera proyección). Donde esta línea corta a las diferentes aristas del tetraedro tienes los puntos N3, P3, R3, S3, T3 y V3, que son los puntos de intersección del plano paralelo a la línea de tierra con el octaedro vistos en tercera proyección. Date cuenta que R3 y N3 coinciden en la tercera proyección.
- Traza paralelas a la línea de tierra que pasen por T3, V3, S3 y P3. Donde estas paralelas cortan a las mismas líneas sobre las que se encuentran en la proyección vertical tienes T2, V2, S2 y P2. Esta parte puede resultar un poco compleja. Para aclararlo un poco, si T3 se encuentra en el segmento que une B3 y E3, entonces T2 estará en el segmento que une B2 con E2… y así con todos los demás. Luego, una vez que tienes las proyecciones verticales de los puntos, dibuja perpendiculares a la línea de tierra que pasen por T2, V2, S2 y P2. Donde esas perpendiculares cortan a las líneas que les corresponden en la proyección horizontal tienes T1, V1, S1 y P1.
- Los puntos R3 y N3 no los puedes hallar como los otros porque al trazar la paralela, esta contiene a las líneas, por lo que es imposible saber así donde cortan. Así pues, lo primero que debes hacer es una perpendicular a la línea de tierra que pase por ellos. Recuerda que N3 y R3 coinciden en la tercera proyección, por lo que solo tienes que hacer una. Donde esta perpendicular corta a la línea de tierra tienes el punto N’. A continuación traza un arco con centro en O y radio hasta N’ hasta cortar a la perpendicular a la línea de tierra que pasa por O. Ese arco corta a esa perpendicular en N.
- Traza una paralela a la línea de tierra que pase por N. Donde esa paralela corta a las aristas del octaedro que son paralelas al plano horizontal tienes los puntos N1 y R1. Si trazas perpendiculares a la línea de tierra que pasen por esos puntos, obtienes N2 y R2 sobre la proyección vertical de esas líneas.
- Para terminar, solo debes unir los puntos para dibujar la sección plana. Es importante marcar correctamente las partes visibles y ocultas de la misma. En la proyección vertical serán ocultos los segmentos que unen V2 con T2, T2 con R2 y R2 con S2. Por otra parte, en la proyección horizontal son ocultos los segmentos que unen R1 con S1, S1 con P1 y P1 con N1.
