El hexaedro o cubo es un sólido poliédrico formado por seis caras que son cuadrados perfectos iguales. Uniendo sus vértices dos a dos se obtienen cuatro diagonales que son iguales, oblicuas y que además se cortan en el centro geométrico del mismo. A partir de la arista de una de sus caras se puede conocer la diagonal de la cara, y a través de ella, la diagonal del hexaedro.
Como dibujar un hexaedro con una de sus caras apoyadas en el plano horizontal conociendo la arista
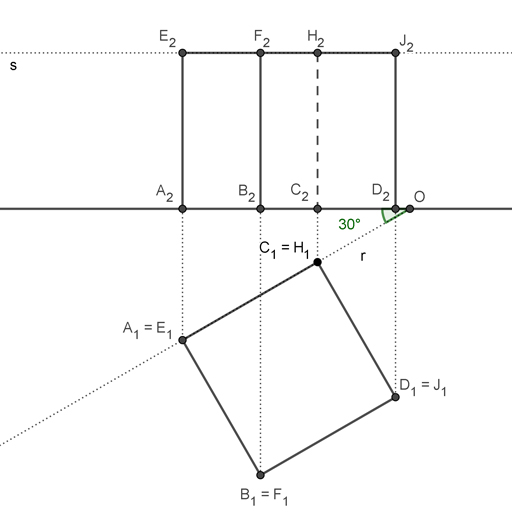
Para este tipo de ejercicios se conoce la longitud de la arista de una de las caras del hexaedro. Al tratarse de un ejercicio realmente sencillo, se suele solicitar que la base tenga cierto ángulo, que coincida con determinados elementos, o cualquier tipo de complicación parecida. El cualquier caso, el proceso es realmente sencillo. Empieza por dibujar la base, si no recuerdas como, te recomiendo visitar la entrada donde hablo de como dibujar un cuadrado conociendo su lado. Para darle un poco de gracia, vamos a considerar que dos de los lados del hexaedro forman un ángulo de 30º respecto a la línea de tierra. La arista del hexaedro mide 6cm.
- Empieza por marcar un punto cualquiera sobre la línea de tierra al que llamaremos O. A partir de O traza una línea que forme los 30º que se solicitan en este ejercicio. A esa recta puedes llamarla r para identificarla.
- Sobre la recta r marca un punto cualquiera al que llamaremos A1.
- Dibuja una perpendicular a la línea de tierra que pase por A1. Donde esa perpendicular corta a la línea de tierra tienes A2. Si prolongas esa línea, y a partir de A2 mides sobre ella la longitud de la arista hallas el punto E2.
- Traza una perpendicular a r que pase por A1. Sobre esa perpendicular mide la longitud de la arista para hallar B1.
- Marca una perpendicular a la línea de tierra que pase por B1. Donde esa perpendicular corta a la línea de tierra tienes B2.
- Traza una paralela a la línea de tierra que pase por E2. Para referirnos a ella, llamaremos s a esta perpendicular. Donde s corta a la perpendicular que pasa por B1 tienes el punto F2.
- A partir de A1 mide la distancia de la arista. De esa manera obtienes C1. Traza ahora una perpendicular a la línea de tierra que pase por C1. Donde esa perpendicular corta a la línea de tierra tienes C2, y donde corta a s tienes H2.
- Con centro en C1 y radio igual a la arista traza un arco. Luego traza otro arco con centro en B1 y el mismo radio. Donde ambos arcos se cortan tienes el punto D1.
- Dibuja una perpendicular a la línea de tierra que pase por D1. Donde esa perpendicular corta a la línea de tierra tienes D2, y donde corta a s tienes J2.
Sección principal del hexaedro
El hexaedro tiene seis secciones principales. Estas son rectángulos formados por dos lados que son las diagonales de una cara, y dos aristas del mismo. Así pues, puedes dibujar la sección principal del cubo con solo conocer la medida de la arista. Para ello debes hacer lo siguiente:
- Dibuja un cuadrado con la longitud de la arista que conoces. Sus vértices serán A, B, C y D.
- Con centro en C y radio hasta B, traza un arco que corta a la prolongación del lado CD en el punto E.
- El rectángulo que determinan los lados AC y DE es la sección principal del hexaedro.
Desarrollo del cubo
El desarrollo del cubo o hexaedro son seis cuadrados unidos por sus lados de tal manera que cada dos de ellos comparten un lado. Hay varias formas de realizar este desarrollo. A continuación tienes algunas de ellas. Por supuesto, no son todas las posibilidades que hay, seguro que ahora mismo se te está ocurriendo alguna que no aparece aquí abajo.
