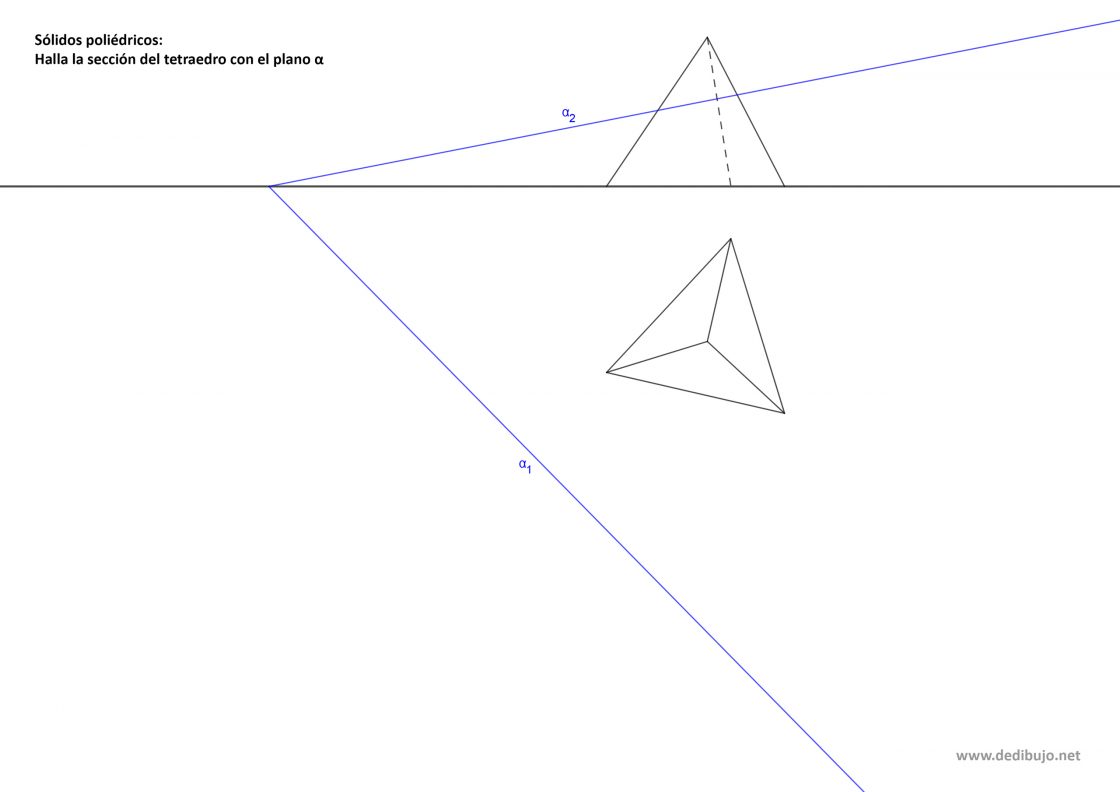
Un ejercicio común cuando hablamos del sistema diédrico en lo que se refiere a segundo de bachillerato, y que te puedes encontrar en tus exámenes de acceso a la universidad es la sección que se produce mediante un plano oblicuo. Para que te sea más fácil realizar este ejercicio, a continuación tienes una lámina que puedes imprimir. Tu punto de partida será algo parecido a lo siguiente:
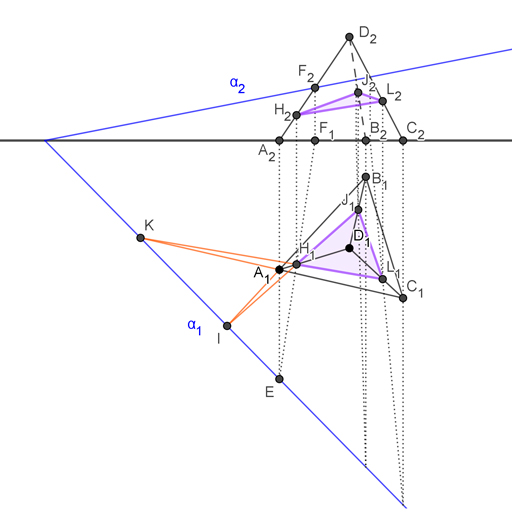
- El primer paso es empezar por poner nombre a los cuatro vértices del tetraedro, para poder referirnos a ellos. De esa manera tienes los puntos A, B, C y D, representados por sus proyecciones vertical y horizontal A1, A2, B1, etc…
- Aunque pienses que es un ejercicio complejo, si sabes realizar intersecciones en sistema diédrico (y a estas alturas deberías ser capaz de hacerlas sin problema), el problema no es tan difícil. Empieza con la intersección del plano α con la arista representada por el segmento AD. Veamos como:
- Incluye el segmento AD en un plano proyectante vertical. Para ello dibuja una perpendicular a la línea de tierra que pase por A2. Donde esta perpendicular corta a la traza horizontal del plano α tienes el punto E.
- A este plano proyectante puedes llamarlo β. Lo que debes hacer ahora es hallar la intersección de β con el plano α. Eso lo consigues dibujando la línea que une los puntos donde ambas trazas se cortan. Donde la traza vertical de α corta a la traza vertical de β tienes F2. Si realizas una perpendicular a la línea de tierra que pase por F2 obtienes F1, que es la proyección horizontal del punto F.
- Ahora une E con F1. Esa es la proyección horizontal de la intersección de los planos α y β. Donde esa línea corta al segmento AD tienes H1. Si levantas una perpendicular a la línea de tierra que pase por H1, donde esa perpendicular corta a la proyección vertical del segmento AD tienes H2. El punto que representan H1 y H2 es el primer punto de intersección del plano oblicuo con el tetraedro.
- El siguiente paso será hallar la intersección del plano α con la arista que representa el segmento BD. Puedes realizarlo repitiendo los pasos que te acabo de explicar más arriba, pero quiero explicarte un sistema alternativo más rápido.
- Prolonga la línea que une A1 con B1 hasta cortar a la traza horizontal del plano en el punto I.
- Dibuja una recta que pase por H1 y el punto I y prolóngala hasta cortar al segmento que forman B1 y D1. El punto donde corten será el punto J1. Con este proceso estás determinando un plano que pasa por I, A1 y H1. Por tanto la intersección de ese plano con α es al mismo tiempo la intersección con el tetraedro.
- Levanta una perpendicular a la línea de tierra que pase por J1 hasta cortar al segmento que forman B2 y D2. Ese punto de intersección será J2.
- Lo siguiente será hallar el último punto de intersección.
- Traza una recta que pase por A1 y C1 hasta cortar a la traza horizontal del plano en el punto K.
- Dibuja una línea que pase por K y H1 hasta cortar al segmento que une C1 y D1. Ese punto de intersección será L1.
- Realiza una perpendicular a la línea de tierra que pase por L1 hasta cortar a la arista que representan C2 y D2. El punto de corte será L2.
Aquí abajo he hallado también los puntos J y L mediante planos proyectantes, para que puedas comprobar que el resultado es el mismo. Te recomiendo ponerlo a pantalla completa y hacer zoom, porque las líneas y los puntos están muy juntos.
