Ángulo que forman dos planos en sistema diédrico, tipos y ejemplos

Al igual que pasaba entre distancias en sistema diédrico, cuando hablamos del ángulo que forman dos planos en sistema diédrico, nos referimos a medido en perpendicular desde la traza que forma la intersección de ambos planos. Ten en cuenta que siempre (o casi siempre) se hace referencia al ángulo agudo, por lo que su valor se va a encontrar comprendido entre los 0º y los 90º.

Planos que forman 90º con los planos proyectantes

Ángulo que forma un plano paralelo al plano vertical con el plano proyectante horizontal

Como puedes ver aquí abajo, el ángulo que forman será siempre de 90 grados.

Ángulo que forma un plano paralelo al plano horizontal con el plano proyectante vertical

Este tipo de planos siempre formarán un ángulo de 90 grados respecto al plano proyectante vertical, como puedes ver aquí abajo.

Ángulo que forma un plano de perfil con los planos proyectantes

Los planos de perfil siempre forman ángulos de 90 grados con los planos proyectantes, como se puede verificar aquí abajo.

Como hallar el ángulo que forma un plano oblicuo con el plano horizontal

¿Recuerdas la recta de máxima pendiente? Es aquella que estando contenida en un plano forma el ángulo máximo con el plano horizontal. Pues gracias a ella puedes averiguar el ángulo que forma un plano oblicuo con el plano horizontal.

Por un punto cualquiera de la traza horizontal del plano al que puedes llamar H₁, traza una perpendicular a la misma. Esta perpendicular corta a la línea de tierra en el punto V₁.
Levanta una perpendicular a la línea de tierra por H₁ hasta cortar a la línea de tierra en H₂. Por otra parte, traza una perpendicular a la línea de tierra que pase por V₁ hasta cortar a la traza vertical del plano en V₂.
Uniendo H₂ con V₂ obtienes la proyección vertical de la recta de máxima pendiente. Si unes H₁ con V₁ puedes hallar la proyección horizontal de la recta de máxima pendiente.
Dibuja una recta perpendicular al segmento que une H₁ con V₁ y que pase por V₁.
Con centro en V₁ y radio hasta V₂ dibuja un arco que corte a la perpendicular anterior en el punto V’
El ángulo que forman V₁, H₁ y V’ es el ángulo que forma el plano con el plano horizontal en verdadera magnitud.

Ángulo que forma un plano oblicuo con el plano vertical

Este caso es muy similar al anterior, pero con la diferencia de que en esta ocasión la recta que te va a ayudar a averiguar el ángulo es la recta de máxima inclinación. Esta recta es la que, estando contenida en un plano, forma el ángulo máximo con el plano proyectante vertical.

Por un punto cualquiera V₂, realiza una perpendicular a la traza vertical del plano. Esta recta cortará a la línea de tierra en H₂.
Traza una perpendicular a la línea de tierra por V₂ hasta cortar en V₁. Luego traza una perpendicular a la línea de tierra que pase por H₂ hasta cortar a la traza horizontal del plano en H₁.
Ahora realiza una paralela a la traza vertical del plano que pase por H₂.
A continuación dibuja un arco con centro en H₂ y radio hasta H₁ hasta cortar a la paralela anterior en H’
El ángulo que forman H’, V₂ y H₂ es el ángulo que forma el plano oblicuo con el plano proyectante vertical.

Cómo dibujar un plano que forma un ángulo α con el plano horizontal

Este tipo de problemas son muy comunes. Se te proporciona un ángulo determinado α (en este caso supondremos un valor de 45º) y se te pide dibujar un plano que forme ese ángulo con el plano horizontal. Si no te proporcionan más datos, hay infinitas soluciones, ya que el plano podría girar sobre un eje sin variar el ángulo. Por ejemplo, podrías solucionarlo dibujando un plano proyectante vertical que formara ese ángulo.

Aquí abajo tienes la demostración. Puedes mover el punto H₁ y cualquiera de los planos resultantes mantendría el ángulo α con el plano horizontal.

Así pues, vamos a complicarlo un poco más.

Dibujar un plano que forma un ángulo α con el plano horizontal y que contiene a la recta r

Lo primero que debes recordar es que cuando una recta está contenida en un plano, sus trazas se encuentran sobre las trazas del plano. Por ese motivo, solo necesitas dos puntos más sobre las trazas para poder dibujar el plano. Para este ejercicio el ángulo α solicitado será de 60 grados. Tu punto de partida será parecido a esto:

Marca un punto cualquiera A sobre la recta, representado por sus proyecciones A₁ y A₂. El punto B será la intersección de la línea que une A₁ y A₂ con la línea de tierra.
Dibuja un ángulo α sobre la línea de tierra que pase por A₂, de esa manera determinas el punto C.
Con centro en A₁, dibuja una circunferencia de radio BC. Date cuenta de que esa circunferencia determina la base de las infinitas rectas de máxima pendiente que se pueden dibujar que pasen por A₂. Pero de todas ellas, al ser la traza perpendicular a la recta, solo habrá dos soluciones que pasen por H₁.
Supongo que a estas alturas ya habrás descubierto que esos dos puntos son los que determinan las rectas tangentes a la circunferencia y que pasan por H₁. Así obtienes los puntos D y E.
Si unes H₁ con D y lo prolongas hasta cortar la línea de tierra tienes la traza horizontal del plano β. Donde esa línea corta a la línea de tierra tienes O, que es el vértice del plano. Si unes O con V₂ tienes la traza vertical del plano β.
Como te explicaba antes, hay dos soluciones posibles. La otra sería uniendo H₁ con E hasta cortar la línea de tierra en el punto O’. Esa será la traza horizontal del plano γ. Si unes O’ con V₂ obtienes la traza vertical del plano γ.

Como trazar un plano que forma un ángulo α con el plano vertical y contiene a la recta r

Este ejercicio es muy similar al anterior. La diferencia está en que los pasos los vas a realizar tomando como referencia el plano vertical. Por hacer algo distinto, en este caso vamos a considerar que el ángulo α es de 30 grados. Tu punto de partida será algo similar a esto:

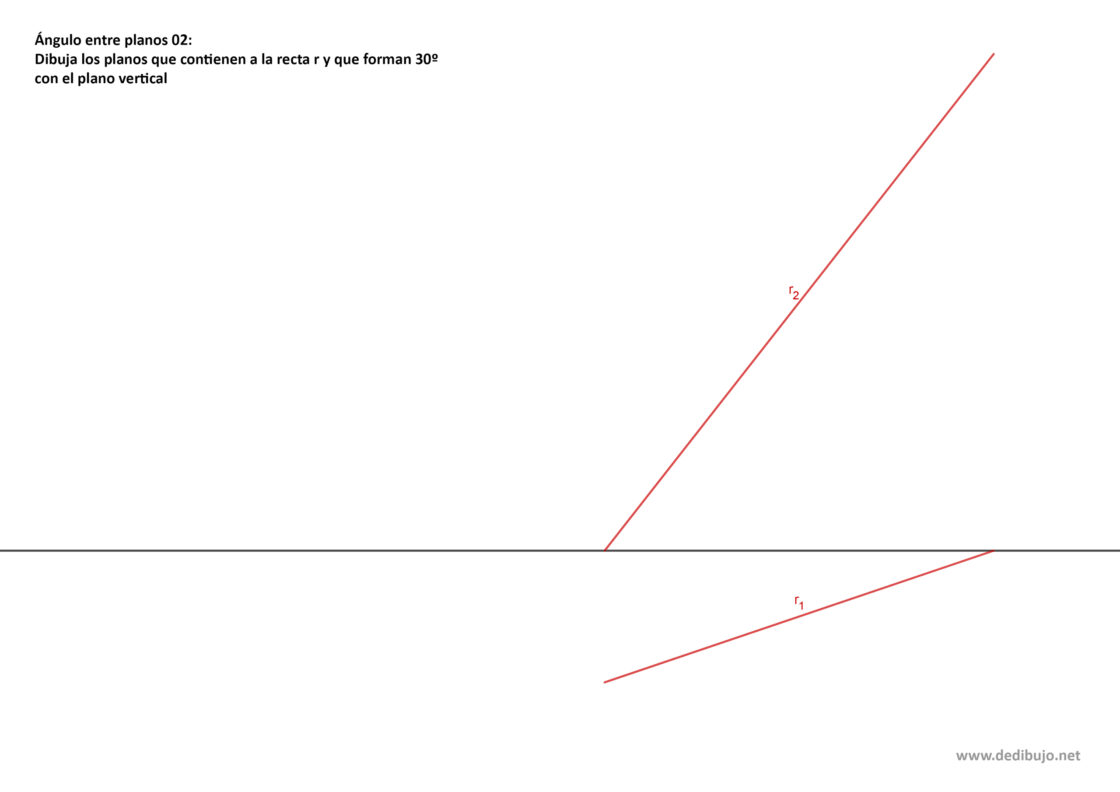
Empieza marcando un punto cualquiera A, representado por sus proyecciones A₁ y A₂ sobre la recta r. El punto de intersección de la línea que une A₁ con A₂ es el punto B.
Dibuja una línea que forme un ángulo α con la línea de tierra y que pase por A₁. De esa manera obtienes el punto C.
Ahora traza una circunferencia con radio BC y centro A₂. Ese círculo determina la traza de todas las rectas de máxima inclinación que forman un ángulo α y que pasan por A.
Como la traza formará un ángulo recto con la recta de máxima inclinación y además pasará por V₂, la solución la obtienes hallando las tangentes a esa circunferencia que pasan por V₂. Esos son los puntos E y F.
Si unes V₂ con E obtienes la traza vertical del plano, y donde esa traza corta a la línea de tierra, el punto O, que es el vértice del plano. Uniendo O con H₁ tienes la traza horizontal del plano. Esa es una de las dos soluciones posibles.
Uniendo V₂ con F tienes la traza vertical del segundo plano posible. Donde esa traza corta a la línea de tierra tienes el punto O’, que es el vértice de ese plano. Ahora uniendo O’ con H₁ obtienes la traza horizontal de ese plano.

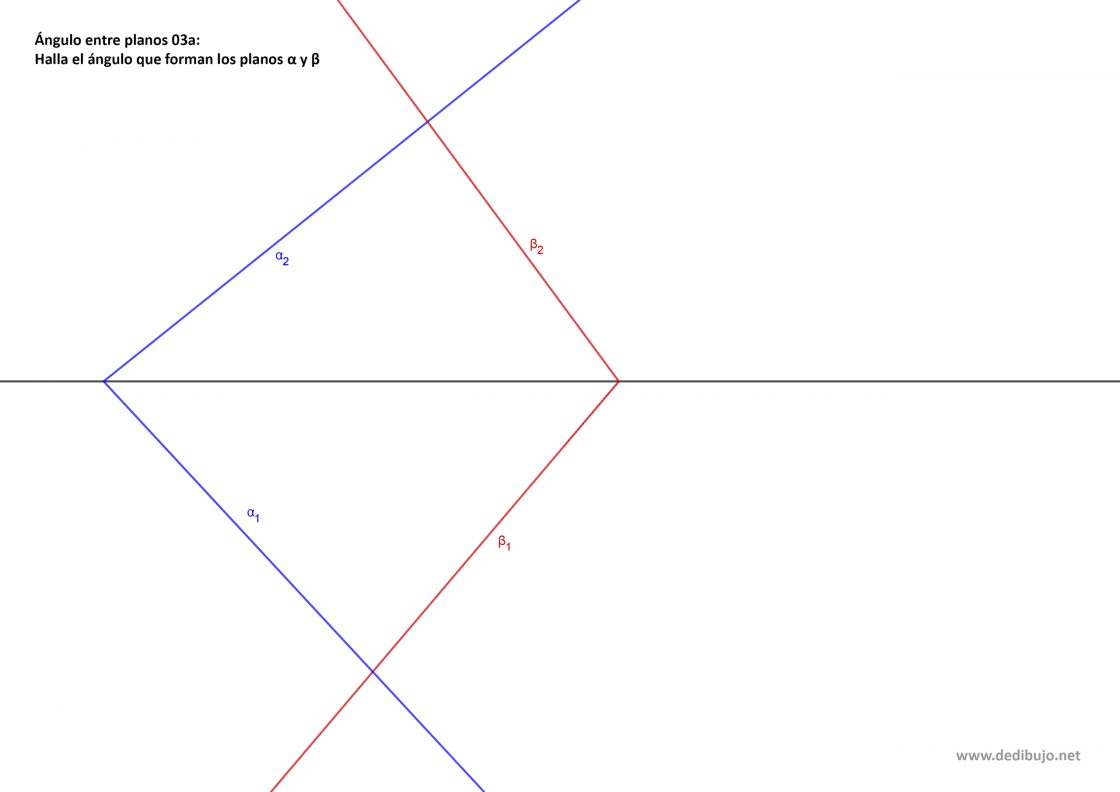
Ángulo que forman dos planos cualquiera

Para explicarte este concepto, primero debes entender como se mide este ángulo. La parte más importante es entender que los ángulos se deben medir siempre en perpendicular. Es decir, si tenemos dos planos α y β, para medir el ángulo que forman debemos hallar la recta intersección. Luego trazamos un plano perpendicular a esa intersección por un punto cualquiera de la misma. Para terminar solo tienes que abatir ese plano, con las rectas que forman el punto que elegiste y los puntos de intersección de los planos. Pero vamos a verlo poco a poco para que lo veas más claro. Tu punto de partida será algo parecido a esto:

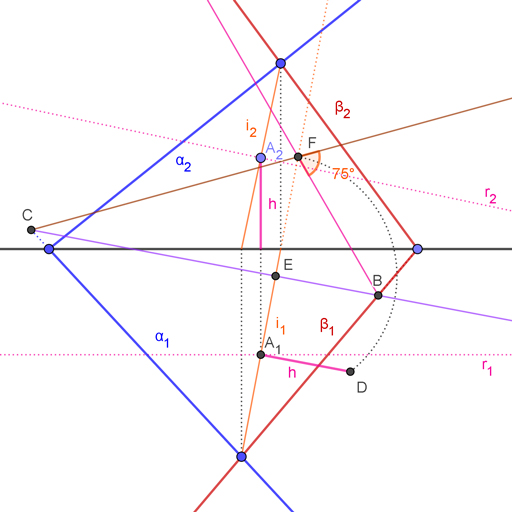
Empieza hallando la intersección entre ambos planos. En este ejemplo lo tienes representado por la recta naranja, a la que llamaremos i, con sus proyecciones i₁ e i₂.
Sobre esta línea, marca un punto cualquiera A, representado por sus proyecciones A₁ y A₂.
El siguiente paso es dibujar un plano perpendicular a esta recta intersección por el punto A. Date cuenta de que al ser perpendicular a la intersección, es por tanto perpendicular tanto a α como β al mismo tiempo. Si no recuerdas como se hace, lo vamos a dibujar con una recta frontal.
Dibuja una recta perpendicular a la recta i₂ que pase por A₂. Esa recta corta a la línea de tierra en el punto H₂. Esta recta la puedes llamar r₂.
Traza una recta paralela a la línea de tierra que pase por A₁ a la que puedes llamar r₁ para identificarla. Luego traza una perpendicular a la línea de tierra que pase por H₂, donde esta perpendicular corta a la paralela tienes el punto H₁, que forma parte de la traza del plano perpendicular a ambos planos y que pasa por A.
Si trazas una recta perpendicular a i₁ que pase por H₁ tienes δ₁, que es la traza horizontal del plano perpendicular. Lo que te interesa ahora es ver donde esa traza corta a las trazas horizontales de los planos α y β para poder realizar la intersección.
El punto donde la traza horizontal δ₁ corta a β₁ tienes el punto B. Por otra parte, donde corta a α₁ tienes el punto C. No te preocupes si B ó C se van detrás del plano vertical, no pasa nada. Solo prolonga las trazas del plano.
Si te das cuenta, realizando el abatimiento del las rectas que forman C y A₁ por un lado y B y A₁ por el otro tienes el ángulo que forman ambos planos. No obstante, recuerda que cuando te piden el ángulo que forman dos planos, por lo general se refieren al agudo.
La dificultad añadida si tienes los planos dispuestos de esta manera es que el abatimiento lo debes realizar hacia arriba en vez de hacia abajo. Pero como vas a ver, el procedimiento es igual.
Empieza midiendo la altura del punto A₂, en este caso representado por el segmento h.
Ahora traza una perpendicular a i₁ que pase por A₁, y sobre ella mide h, obteniendo así el punto D.
El punto de intersección entre i₁ y δ₁ llámalo E. Pues bien, con centro en E y radio hasta D traza un arco hasta cortar a la prolongación de i₁ en F.
Uniendo C con F por un lado y B con F por el otro tienes el abatimiento de las rectas que forman B con A1 y C con A1, que además representan la intersección del plano perpendicular a i con los planos α y β. Así obtienes el ángulo que forman ambos planos, marcado en naranja en este caso.

Método 2

Existe un segundo procedimiento para hallar el ángulo que forman dos planos. Dependiendo de la posición que ocupen las trazas de ambos planos, será más fácil solucionar el problema utilizando un procedimiento u otro. Este segundo método se basa en marcar un punto cualquiera del espacio, y por ese punto trazar perpendiculares a ambos planos.

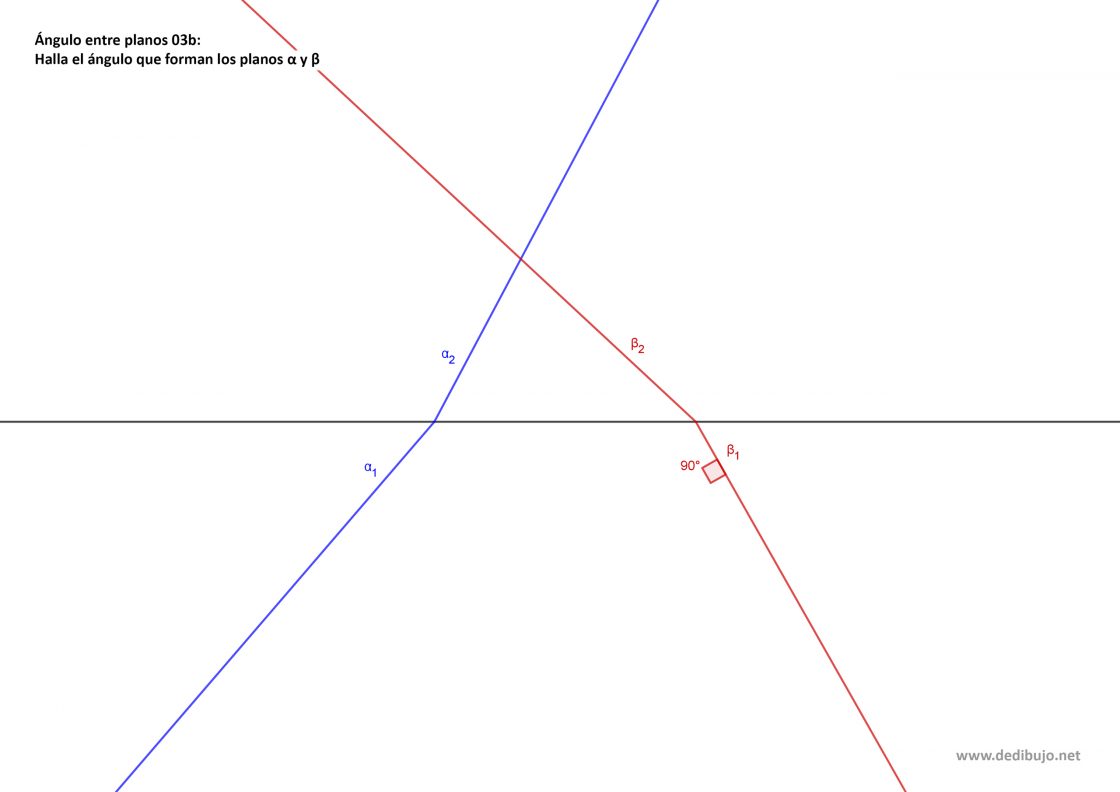
Empieza como te decía, por marcar un punto cualquiera del espacio. En este caso es el punto A, representado por sus proyecciones A₁ y A₂.
El siguiente paso es dibujar rectas perpendiculares a ambos planos, pero que pasen ambas por el punto A. Para ello traza una perpendicular a β₁ que pase por A₁, esa será r₁. Luego dibuja una perpendicular a β₂ que pase por B₂, esa será r₂. Las trazas de la recta r son los puntos B y C, representados por sus proyecciones B₁, B₂, C₁ y C₂.
Ahora toca dibujar una recta perpendicular a α por el punto A. Para ello traza una perpendicular a α₁ que pase por A₁, y luego una perpendicular a α₂ que pase por A₂. Esta será la recta s, representada por sus proyecciones s₁ y s₂. Las trazas de la recta s son D₁ con D₂ y E₁ con E₂.
Lo siguiente será abatir el punto A₁. Para ello dibuja la línea que une B₁ con E₁.
Continua dibujando una perpendicular a la línea que dibujaste en el paso anterior, pero que pase por A₁. Donde esa perpendicular corta a la recta que une B₁ con E₁ tienes el punto F.
Ahora mide la altura del punto A₂, representada en este caso por el segmento h.
Traza una paralela al segmento que une B₁ con E₁ que pase por A₁, y a partir de A₁ mide el segmento h. De esa manera obtienes el punto H.
Con centro en F, y radio hasta H, traza un arco que corte a la perpendicular que pasa por A₁ hasta cortar en el punto J.
Si unes B₁ con J por un lado, y E₁ con J tienes r’ y s’, que son el abatimiento de las rectas r y s. El ángulo que forman estas rectas (marcado aquí en naranja) es el ángulo que forman los planos α y β. En caso de que no sepas que ángulo es el que forman los planos, opta siempre por el ángulo agudo.