Los cambios de plano cuando trabajamos con rectas nos sirven para transformar rectas oblicuas en frontales, horizontales, verticales, de punta y paralelas a la línea de tierra. Esto sirve para hallar sus verdaderas magnitudes y trabajar con mayor comodidad.
Para obtener las proyecciones de una recta tras un cambio de plano es necesario tomar dos puntos como referencia y luego hallar sus nuevas proyecciones en el plano que cambia. Yo te recomiendo que siempre que puedas utilices una traza como uno de esos puntos. De esa manera te ahorrarás mucho trabajo y dolores de cabeza.
Convertir una recta oblicua en frontal con un cambio de plano
Para realizar este ejercicio debes girar el plano vertical hasta que quede paralelo a la recta. Por lo tanto lo que no cambiará será la altura de los elementos.
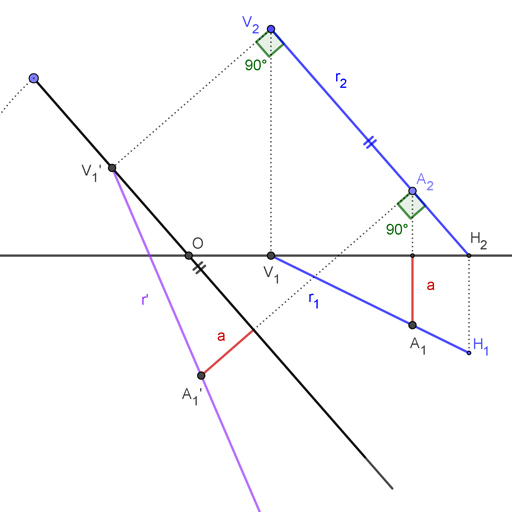
Para este ejercicio te proporcionan una recta oblicua, representada por las proyecciones vertical y horizontal. En este caso es la recta r, marcada aquí en azul. Tu punto de partida pues será algo similar a este:
- Empieza por dibujar una recta paralela a r1, ya que lo que pretendes es convertir la recta en frontal. Esa será la nueva línea de tierra una vez girado el plano vertical.
- A continuación dibuja una perpendicular a esa recta que pase por H1. De esa manera determinas H2‘, que corresponde a la nueva proyección vertical de la traza horizontal de la recta una vez girado el plano.
- Marca una punto cualquiera A que utilizarás como referencia, y delimita sus proyecciones vertical y horizontal como A2 y A1 respectivamente. Acto seguido mide la altura de A2, que vas a necesitar en el paso siguiente. A esa altura puedes llamarla h.
- Ahora traza una perpendicular a la nueva línea de tierra que pase por A1 a partir del punto de intersección de esa recta con la nueva línea de tierra debes medir la altura del punto A2, que era igual al segmento h. Así estás delimitando A2‘, que será la nueva proyección vertical de la recta.
- Para terminar, dibuja la recta que pasa por H2‘ y A2‘. Esa es la nueva proyección vertical de la recta. Date cuenta de que al tratarse de una recta frontal, no hay traza vertical de la recta.
Cambiar de plano para convertir una recta oblicua en horizontal
Para convertir una recta oblicua en horizontal gracias a un cambio de plano, el plano que debes mover es el horizontal. El proceso consiste en situar el plano horizontal de tal manera que quede paralelo a la recta. De esa manera, al proyectar sobre el plano, la recta pasa a ser horizontal. Lo importante en este proceso es recordar que al cambiar el plano de lugar, los alejamientos no se modifican, tan solo cambia la cota.
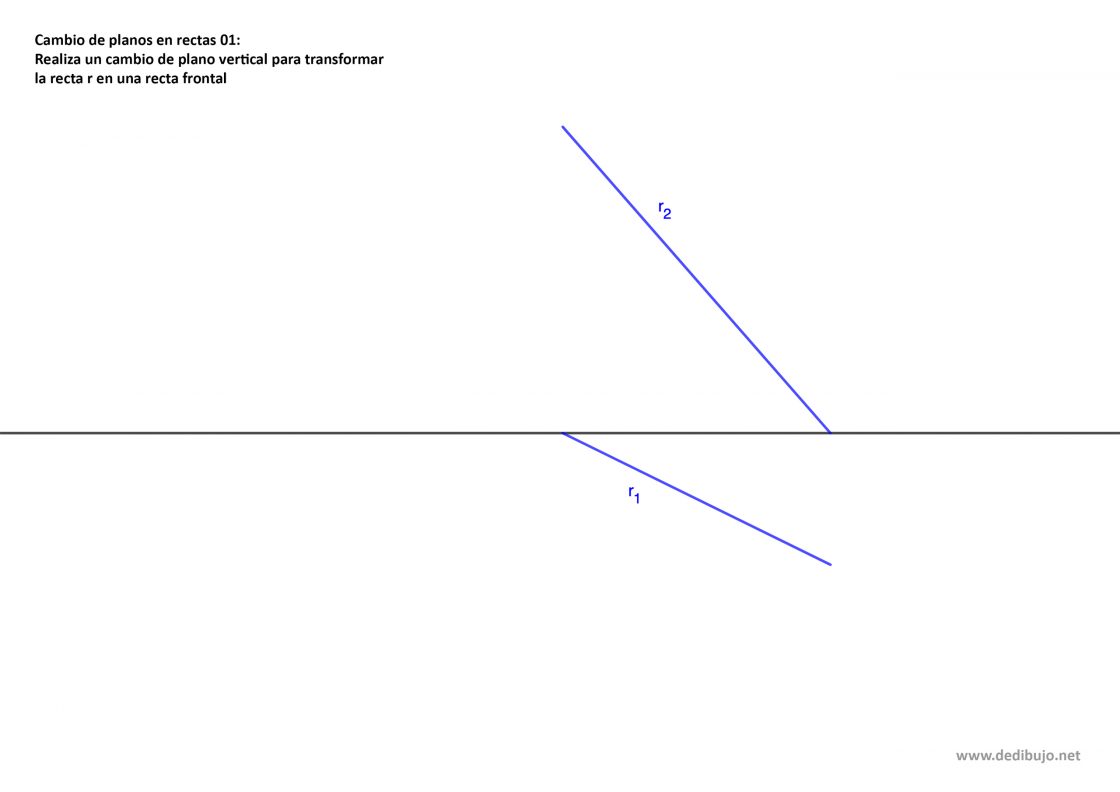
En este caso, lo que se pide es transformar la recta r en una recta horizontal. Tu punto de partida será algo parecido a esto:
Para ello debes hacer lo siguiente:
- Para cambiar de plano una recta debes mover dos puntos. En este caso te recomiendo usar la traza vertical de la recta, definida por V1 y V2 y un punto cualquiera al que llamaremos A, definido por sus proyecciones A1 y A2.
- Como quieres transformar la recta en horizontal, la nueva posición de la línea de tierra debe ser paralela a la proyección vertical de la recta. Así pues, por un punto cualquiera al que llamaremos O de la línea de tierra, traza una paralela a la proyección vertical de la recta.
- Traza una perpendicular por V2 hasta cortar a la nueva línea de tierra. Ese punto será V1‘
Girar el plano vertical para transformar una recta horizontal en una de punta
Para transformar una recta horizontal en una recta de punta debes hacer un cambio de plano vertical. Al hacer este procedimiento, la altura de los puntos de la recta no varía en ningún momento.
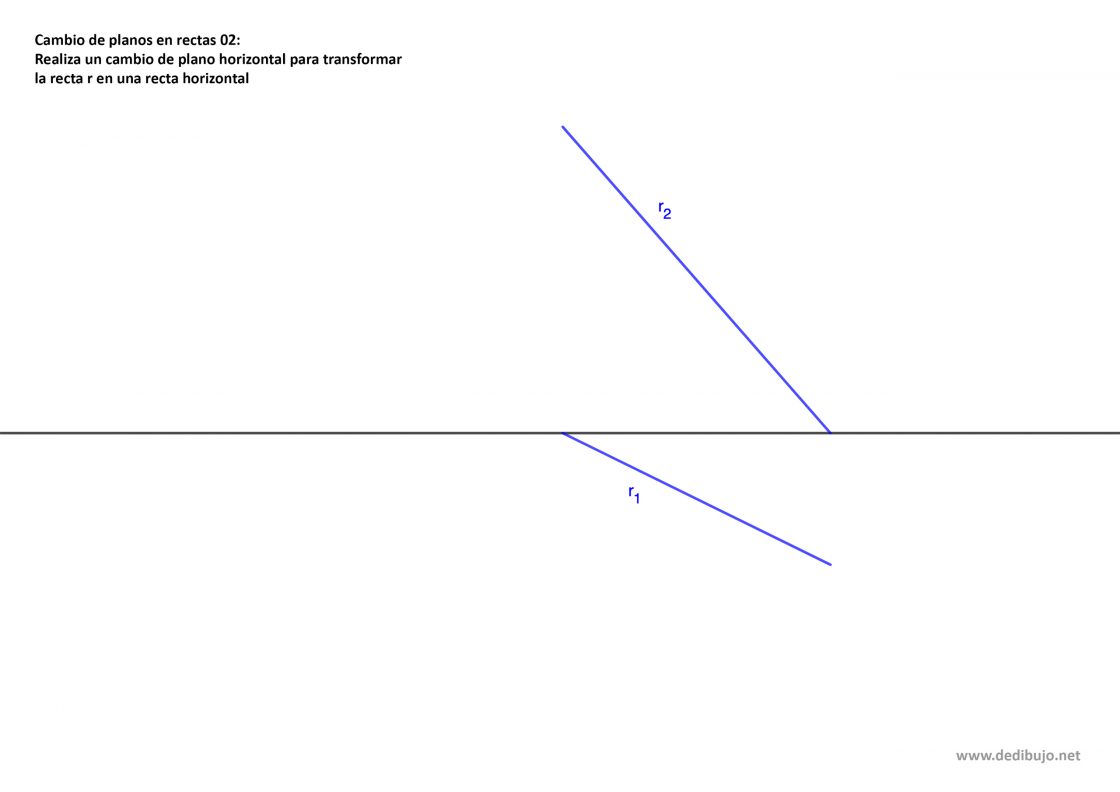
En este caso conoces una recta horizontal representada por sus proyecciones r1 y r2. Tu punto de partida será parecido a esto:
- Como una recta de punta tiene su proyección horizontal perpendicular a la línea de tierra, la nueva línea de tierra debe tener esa posición. Así pues, dibuja una recta perpendicular a la proyección horizontal de la recta por un punto cualquiera O de la línea de tierra.
- Donde esa perpendicular corta a la proyección horizontal de la recta tienes V1‘, que será la nueva proyección horizontal de la traza de la recta una vez realizado el cambio de plano.
- Mide la altura de la traza vertical de la recta, representada aquí por el segmento h. Luego lleva esa misma altura a partir de V1‘ para determinar V2‘, la nueva traza vertical de la recta de punta.
Transformar una recta frontal en una vertical cambiando el plano horizontal
En este caso, lo que no varía en ningún momento es el alejamiento de los puntos, ya que lo que se cambia es el plano vertical.
- Una recta vertical tiene su proyección vertical perpendicular a la línea de tierra. Por lo tanto, lo primero que debes hacer es dibujar la nueva línea de tierra. Para ello realiza una línea perpendicular a la proyección vertical de la recta por un punto cualquiera O de la línea de tierra.
- El punto donde esa perpendicular corta a la propia proyección vertical de la recta llámalo H2‘, ya que será la nueva proyección vertical de la traza de la recta.
- Mide el alejamiento de la traza horizontal del plano al que llamaremos a. En ningún caso el alejamiento varía, por lo que será este valor el que utilizaremos para hallar la nueva traza horizontal.
- A partir de H2‘ mide el alejamiento sobre la proyección vertical de la recta, obteniendo de ese modo el punto H1‘, que representa la nueva proyección horizontal de la traza horizontal de la recta vertical.
Transformar una recta horizontal en paralela a la línea de tierra cambiando el plano vertical
En este tipo de ejercicios la altura de los puntos no varía en ningún momento. Para hacer el cambio de plano no necesitas ningún punto de referencia. Yo los he puesto aquí para ilustrar la operación, pero realmente lo único que necesitas saber es a que altura está la proyección vertical sobre la línea de tierra. Tu punto de partida será el mismo que antes, es decir, algo muy parecido a esto:
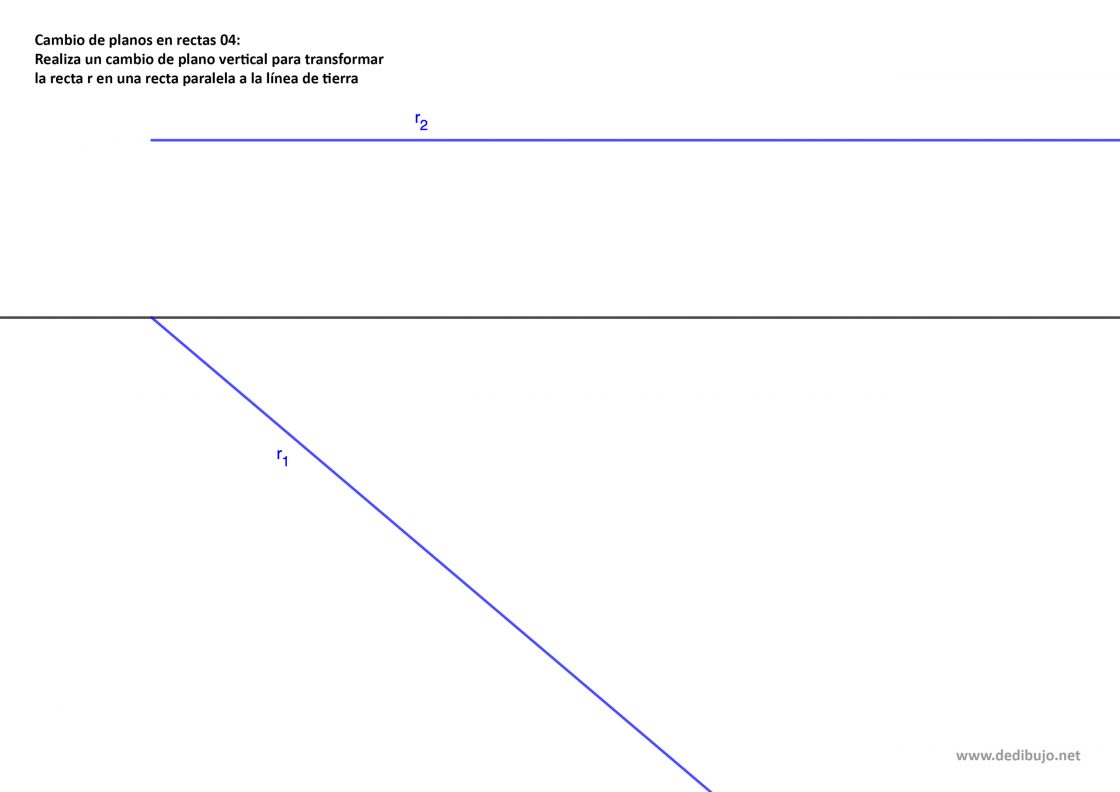
- Dibuja una recta paralela a la proyección horizontal de la recta que pase por un punto cualquiera que puedes llamar O, esa será la nueva línea de tierra.
- Mide la altura a la que se encuentra la proyección vertical de la recta. En este caso representada por el segmento h.
- Dibuja una paralela a la nueva línea de tierra que se encuentre a una distancia h sobre ella. Esa será la nueva proyección vertical de la recta. Ten en cuenta que la proyección horizontal no cambia.
Aquí abajo los puntos A y B los he puesto solo para aclarar como funciona el proceso. No obstante date cuenta de que realmente no los necesitas para nada.
Girar el plano horizontal para transformar una recta frontal en paralela a la línea de tierra
Para este procedimiento el valor que permanece constante es el alejamiento de los puntos. Al igual que en el caso anterior no necesitas ningún punto de referencia. Yo he añadido aquí A y B solo para ilustrar el cambio de plano, pero date cuenta de que lo único que necesitas es conocer el alejamiento de la proyección horizontal de la recta.
Tu punto de partida será parecido a esto:
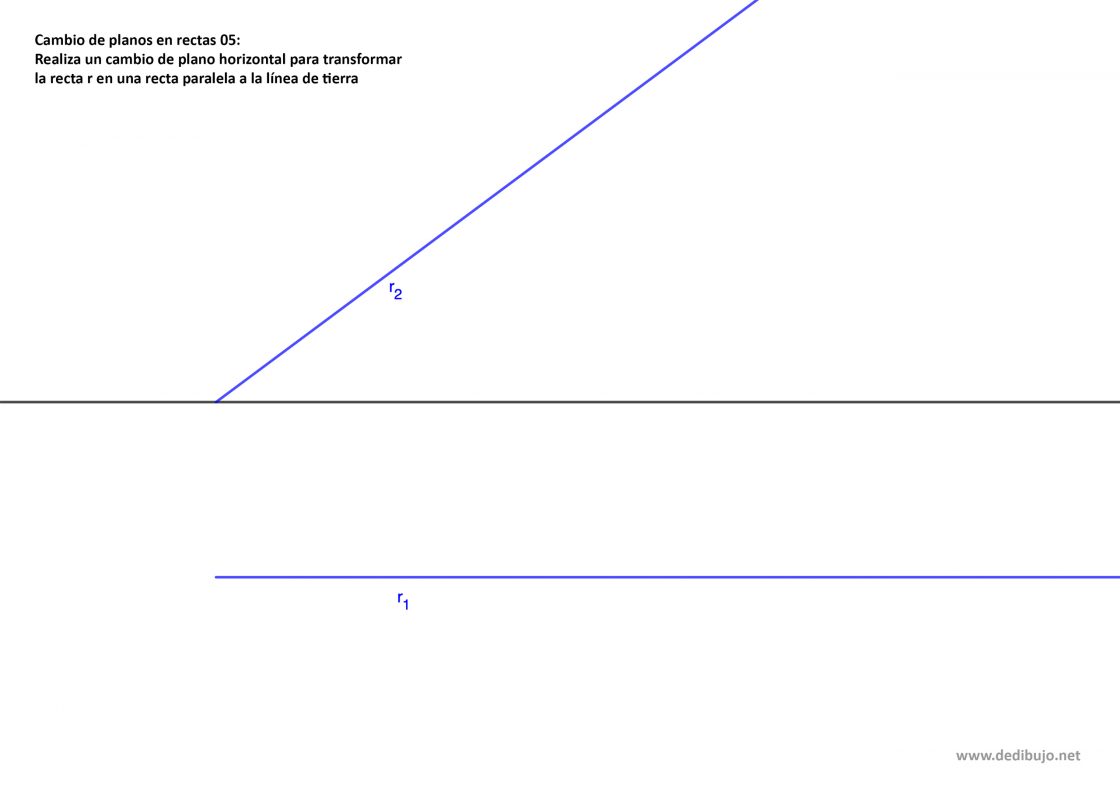
- Mide el alejamiento de la proyección horizontal de la recta a la línea de tierra. En el ejemplo de aquí abajo la tienes representada por el segmento a.
- Por un punto cualquiera O de la línea de tierra traza una paralela a la proyección vertical de la recta. Esa línea será la nueva línea de tierra.
- Para terminar dibuja una paralela a esa línea de tierra que se encuentre a una distancia igual al alejamiento. Esa será la nueva proyección horizontal de la recta. Dependiendo de donde pongas el punto O, la línea de tierra estará más cerca o más lejos de la proyección vertical de la recta.
