Distancias entre puntos, rectas y planos en sistema diédrico

Al hablar de distancia entre puntos, rectas y planos en el sistema diédrico nos estamos refiriendo a la verdadera magnitud de una distancia. Date cuenta de que no puedes medir directamente una distancia utilizando las proyecciones de las formas. Bueno, la excepción es cuando las formas son paralelas a los planos de proyección. Lo más habitual para hallar verdaderas magnitudes y distancias es utilizar algunos métodos operativos que se estudian en segundo de bachillerato, como giros, abatimientos o cambios de plano. En este caso te explicaré otra manera de resolverlos un poco más sencilla, utilizando la perpendicularidad.

Distancia entre dos puntos

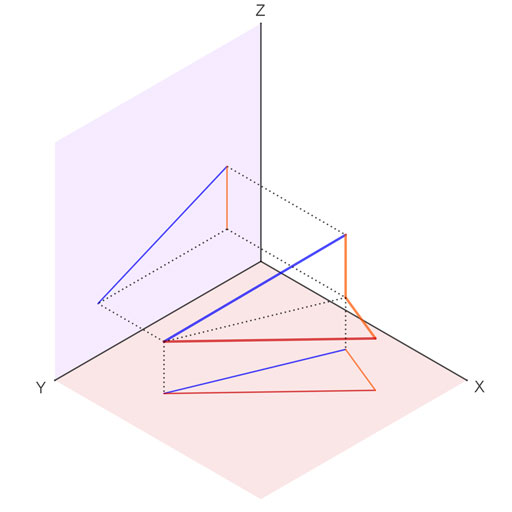
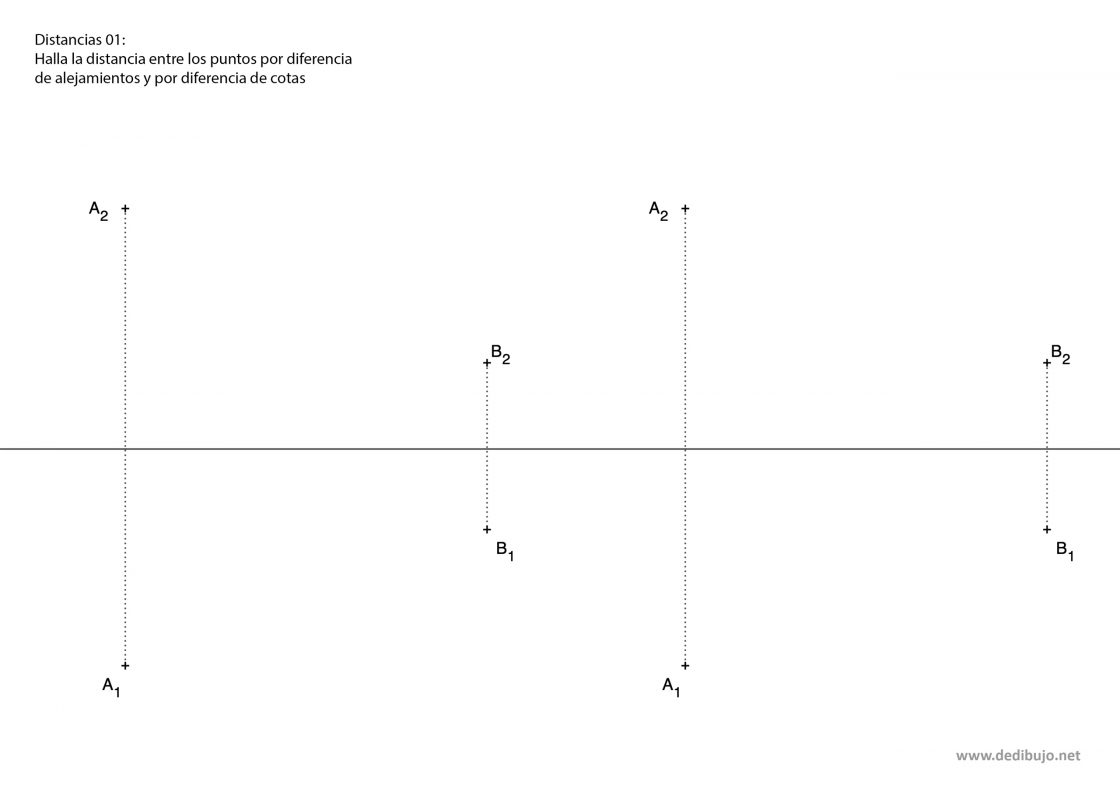
Para determinar la distancia entre dos puntos conocidos A y B tienes que hallar la hipotenusa de un triángulo rectángulo cuyos catetos sean la distancia entre A₁ y B₁ por un lado y la diferencia de alturas por el otro. O bien la distancia entre A₂ y B₂ por un lado y la diferencia de alejamientos por el otro. A continuación tienes un ejercicio para practicar.Te he puesto dos juegos de puntos para que puedas hallar la distancia por diferencia de alejamientos y por diferencia de cotas. En ambos casos, tu punto de partida sería similar a esto:

En el ejemplo de aquí abajo, la distancia entre A1 y C representa la diferencia de alejamientos y el segmento AB representaría la distancia entre los puntos A y B.

Date cuenta de que este proceso lo puedes realizar también sobre la proyección horizontal. Aquí abajo he repetido el ejercicio, pero construyendo el triángulo rectángulo tomando como uno de los catetos la distancia entre A₁ y B₁, y como el otro cateto la distancia entre A₂ y C. Como puedes comprobar, el resultado es el mismo.

Aquí abajo tienes una representación tridimensional de este concepto que espero que te aclare un poco las ideas.

Distancia entre un punto y una recta

Dados un punto P determinado por sus proyecciones P₁ y P₂ y una recta r determinada por sus proyecciones r₁ y r₁. La distancia entre P y r se calcula trazando un plano perpendicular a la recta r que pase por P. Luego debes hallar la distancia entre ese punto de intersección (llamémoslo D) y P del modo habitual.

Para este ejercicio conoces una recta r y un punto P. Tu punto de partida sería algo similar a esto:

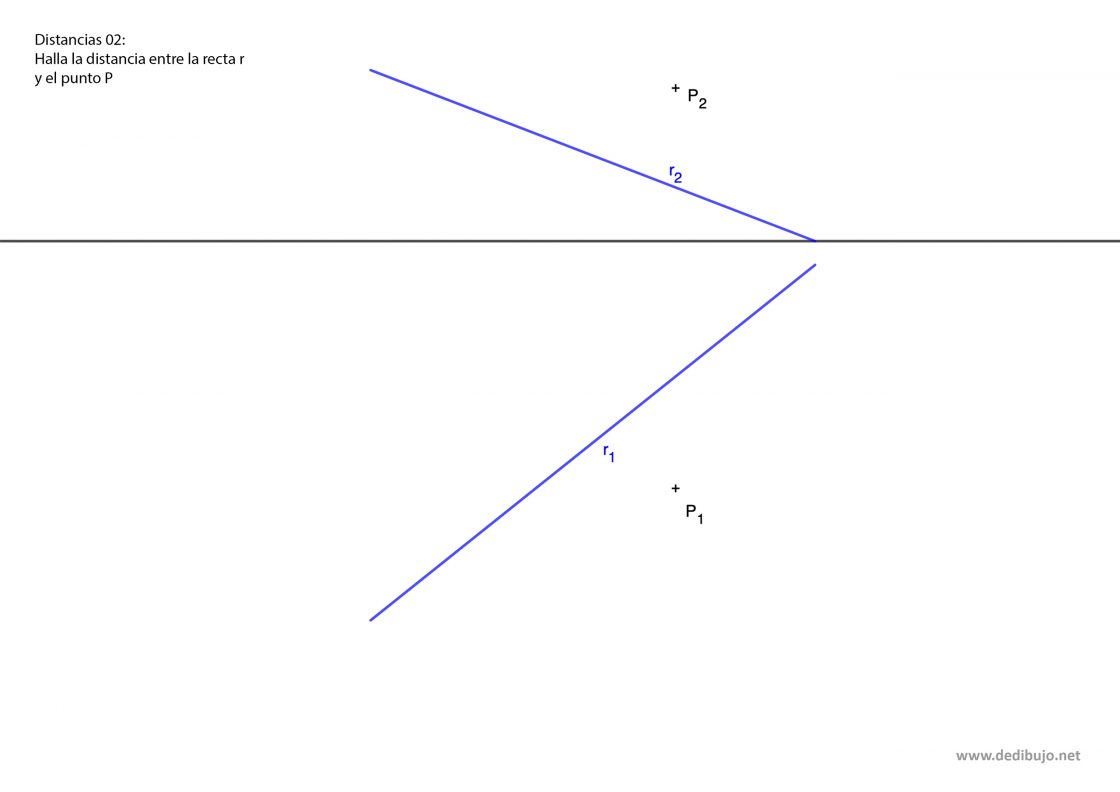
El proceso sería el siguiente:

Dibujar un plano perpendicular a la recta r que pase por P.
1. Para empezar debes dibujar una recta frontal que contenga ese punto. Recuerda que su proyección vertical debe ser perpendicular a la proyección vertical del plano r. El punto donde esa recta corta a la línea de tierra llámalo A₂.
2. Dibuja una perpendicular a la línea de tierra que pase por A₂.
3. Ahora traza una paralela a la línea de tierra que pase por P₁. Donde esta recta corta a la perpendicular del paso 2 tienes el punto A₁. Este punto es la traza horizontal de la recta frontal, y pertenece a la traza horizontal del plano vertical.
4. Lo siguiente que debes hacer es dibujar una recta perpendicular a la traza horizontal del plano y que pase por A₁. Esa recta corta a la línea de tierra en el punto B. Ese punto es común a las trazas del plano perpendicular.
5. Para terminar de dibujar el plano perpendicular, debes dibujar su traza vertical. Para ello dibuja una línea perpendicular a la proyección vertical de la recta y que pase por B.
El siguiente paso será hallar la intersección de la recta r con el plano perpendicular que acabas de dibujar. Para ello debes dibujar un plano proyectante vertical que contenga la recta r.
1. Así pues, empieza dibujando un plano proyectante vertical que contenga a la recta r. Su traza vertical coincidirá con la proyección vertical de la recta r. Su traza horizontal será una perpendicular que pase por C₂.
2. El punto de intersección de las trazas verticales de ambos planos llámalo D₂.
3. La proyección horizontal de ese punto será D₁.
4. Por otra parte, la intersección de las trazas horizontales de ambos planos será E.
5. Si unes D₁ con E con una línea, donde esa línea corta a la proyección horizontal de la recta r tienes el punto F₁.
6. El punto F₁ es la proyección horizontal de la intersección de la recta r con el plano perpendicular. Si levantas una perpendicular a la línea de tierra que pase por F₁, donde esa perpendicular corta a la proyección vertical de la recta tienes F₂.
Ahora para terminar, debes hallar la distancia entre F y P. En este ejemplo utilizaremos la diferencia de alejamientos.
1. Dibuja una paralela a la línea de tierra que pase por F₁. Donde esa paralela corta a la línea que une P₁ con P₂ tienes el punto H. El segmento que une H y P₁ (al que puedes llamar a) es la diferencia de alejamientos.
2. Traza una perpendicular que pase por P₂, y sobre ella mide el segmento a (la diferencia de alejamientos). De esa manera obtienes el punto I.
3. Une F₂ con I, esa es la distancia existente entre la recta r y el punto P.

Distancia de un punto a un plano

Para hallar la distancia entre un punto P y un plano α, debes dibujar una recta perpendicular al plano que pase por ese punto. Luego solo tienes que medir la distancia entre el punto de intersección (vamos a llamarlo D) y P.

Para este ejercicio conoces un plano determinado por sus trazas y un punto P. Tu punto de partida sería parecido a esto:

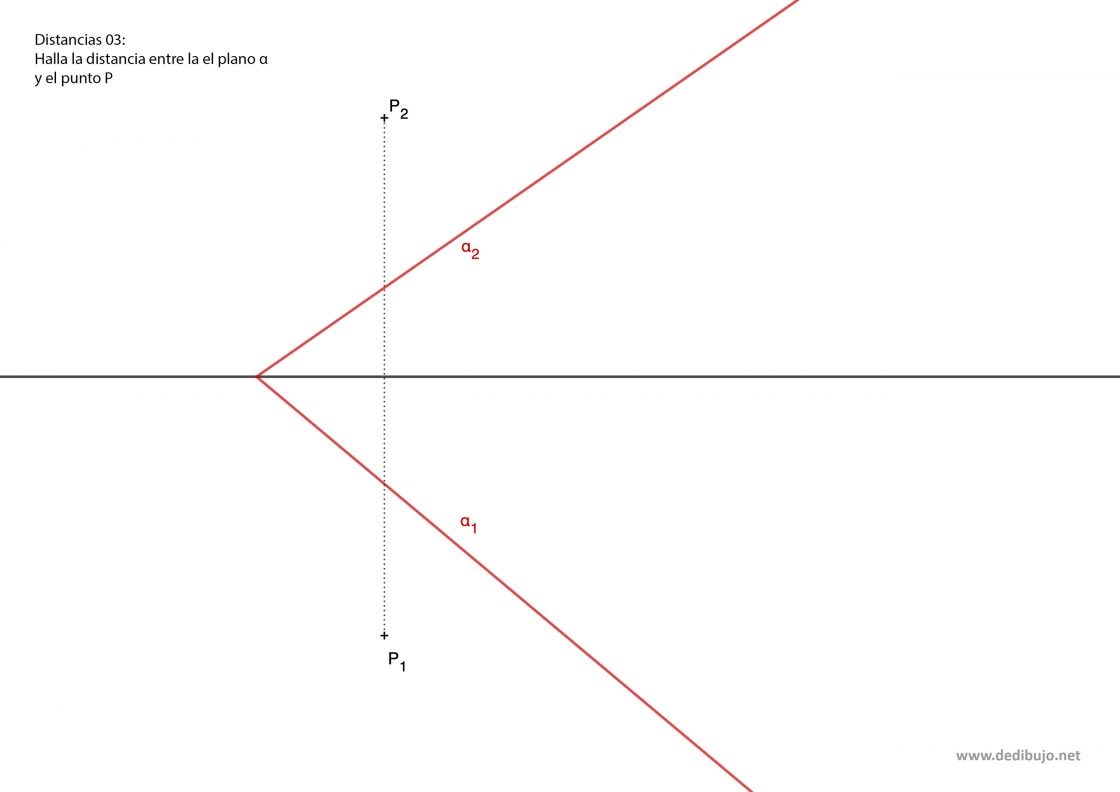
El procedimiento para resolverlo sería el siguiente:

El primer paso es dibujar una recta perpendicular al plano que pase por el punto que conoces, tal como te decía antes.
1. Para ello dibuja una línea perpendicular a la traza vertical del plano que pase por P₂. Esa es la proyección vertical de la recta, llámala r₂.
2. Luego dibuja una línea perpendicular a la traza horizontal del plano que pase por P₁. Así tienes la proyección horizontal de la recta, que puedes llamar r₁.
3. Una vez que tienes las proyecciones de la recta, debes hallar sus trazas. En este caso H₂ y H₁.
Ahora debes encontrar el punto de corte de esa recta que acabas de dibujar con el plano que conoces. Recuerda que el procedimiento es dibujar un plano proyectante vertical que contenga a la recta.
1. Dibuja una línea perpendicular a la línea de tierra que pase por la traza horizontal del plano. Es decir, tanto por H₁ como por H₂. Esa será la traza horizontal del plano proyectante.
2. Donde esa perpendicular corta a la traza horizontal del plano tienes el punto C₁. Ese punto es donde las trazas horizontales de ambos planos se cortan. El punto C₂ coincide con H₂, porque ambos están sobre el plano horizontal.
3. El punto donde la proyección vertical de la recta (que coincide con la traza vertical del plano proyectante vertical), tienes el punto B₂. Ese punto sería donde las trazas verticales se cortan.
4. Traza una línea de B₁ a C₁. Donde esa línea corta a la proyección horizontal de la recta tienes el punto D₁, que es el punto de intersección.
5. Levanta una perpendicular a la línea de tierra que pase por D₁. Donde esa línea corta a la proyección vertical de la recta tienes el punto D₂, que es la proyección vertical de la intersección del plano con la recta.
Ahora que conoces el punto D, el problema se reduce a hallar la distancia entre P y D. Te lo recuerdo de forma breve.
1. Calcula la diferencia de alejamientos entre D y P. en este caso se representa con el segmento a.
2. Dibuja una perpendicular a la proyección vertical de la recta que pase por P₂ y sobre ella mide el segmento a.
3. El punto que obtienes es E.
4. La distancia entre E y D₂ representa la distancia entre el punto y el plano.

Distancia entre dos rectas paralelas

Para calcular la distancia existente entre dos rectas paralelas debes dibujar un plano perpendicular a esas rectas. De ese modo podrás hallar la distancia existente entre ambas rectas calculando la distancia entre los dos puntos de corte. Para este ejercicio te proporcionan dos rectas paralelas, r y s y te piden hallar la distancia existente entre ambas. Tu punto de partida será como esto:

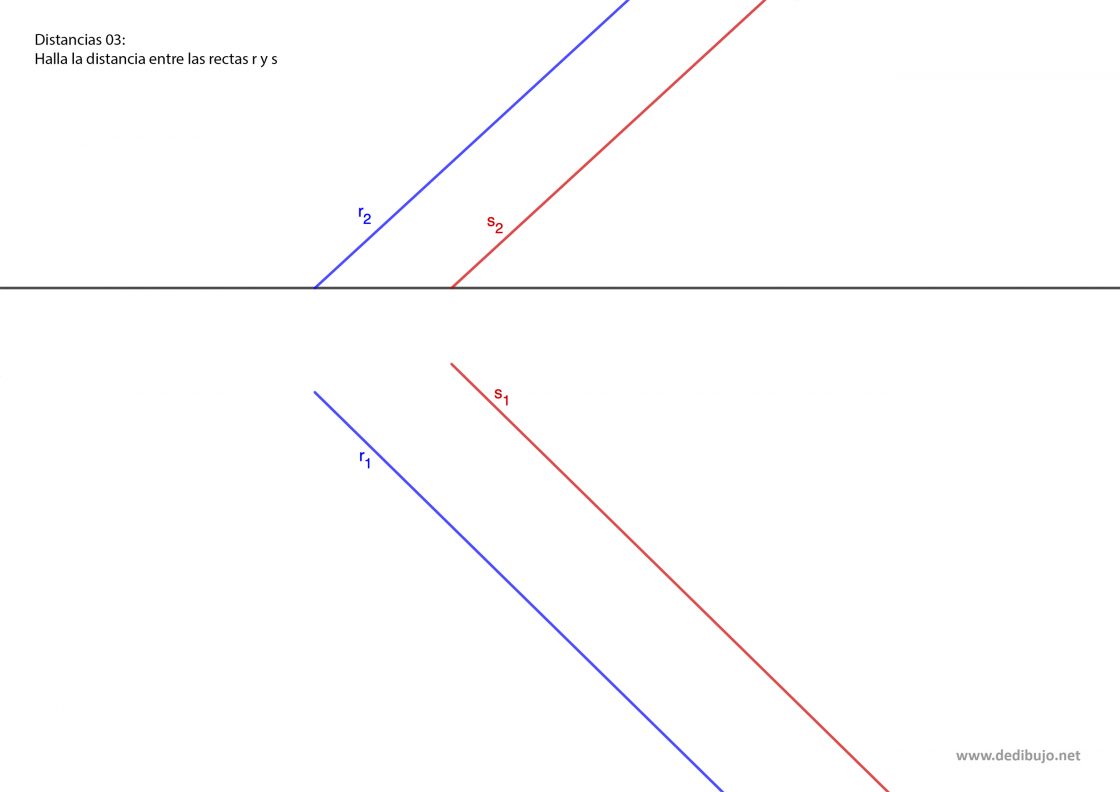
Empieza dibujando las trazas de un plano perpendicular a ambas rectas. Donde las traza vertical de ese plano corta a la proyección vertical de la recta r tienes el punto A₂. Por otra parte, donde esa traza corta a la proyección vertical de la recta s tienes el punto B₂.
Luego dibuja la traza horizontal del plano perpendicular. En el lugar en que esa traza corta a la proyección horizontal de la recta r tienes el punto D₁. A su vez, donde esa traza corta a la proyección horizontal de la recta s tienes el punto F₁.
A continuación debes hallar los puntos de intersección de ese plano con las rectas. Para ir paso a paso, empieza por la recta r. Recuerda que para ello lo más sencillo es un plano proyectante vertical. Así pues, dibuja una línea perpendicular a la línea de tierra que pase por el punto H₂. Donde esa perpendicular corta a la traza horizontal del plano perpendicular tienes el punto C₁.
1. Halla la proyección horizontal del punto A. Eso se hace trazando una perpendicular por A₂ hasta cortar a la línea de tierra. Ese punto llámalo A₁.
2. Une C₁ con A₁ con una línea. Donde esa línea corta a la proyección horizontal de la recta r tienes el punto D₁, que es la proyección horizontal de la intersección de esa recta con el plano perpendicular.
3. Levanta una perpendicular a la línea de tierra que pase por D₁. Donde esa perpendicular corta a la proyección vertical de la recta r tienes del punto D₂, que es la proyección vertical de la intersección de la recta r con el plano perpendicular.
Ahora te toca hallar la intersección de la recta s con ese plano perpendicular.
1. Dibuja una perpendicular a la línea de tierra que pase por H₂‘. El punto donde esa perpendicular corta a la proyección horizontal de la recta s te permite marcar E₁.
2. Halla la proyección horizontal del punto B. Para ello traza una perpendicular a la línea de tierra que pase por B₂. Donde esa perpendicular corta a la línea de tierra tienes el punto B₁.
3. Une E₁ con B₁ usando una línea. Donde esa línea corta a la proyección horizontal de la recta s tienes el punto F₁. Ese punto es la proyección horizontal del punto de intersección con el plano vertical.
4. Traza una perpendicular a la línea de tierra que pase por el punto F₁. Donde esa línea corta a la proyección vertical de la recta s tienes el punto F₂, que es la proyección vertical del punto de intersección de la recta con el plano vertical.
Para terminar, ya solo tienes que hallar la distancia existente entre el punto D y el punto F. En este ejemplo te voy a explicar a hacerlo mediante la diferencia de alejamientos.
1. Traza una paralela a la línea de tierra que pase por F₁. Donde esa línea corta a la línea que une D₂ con D₁ tienes el punto I.
2. La distancia entre el punto I y el punto D₁ representa la diferencia de alejamientos. A ese segmento puedes llamarlo a para identificarlo.
3. Une D₂ con F₂ con una línea. A continuación dibuja una perpendicular a esa línea que acabas de dibujar que pase por D₂.
4. Sobre la perpendicular que dibujaste en el paso anterior mide el tamaño de a (la diferencia de alejamientos). De esa manera obtienes el punto J.
5. Para terminar dibuja el segmento que une J con F₂. Esa es la distancia existente entre ambas rectas.

Distancia entre dos planos paralelos

Para hallar la distancia existente entre dos planos paralelos lo que debes hacer es trazar una recta perpendicular a ambos planos. Luego es tan sencillo como hallar la distancia entre los puntos de intersección de esa recta con ambos planos. Para este ejercicio conoces dos planos, α y β y te piden hallar la distancia entre ambos. Tu punto de partida será como esto.

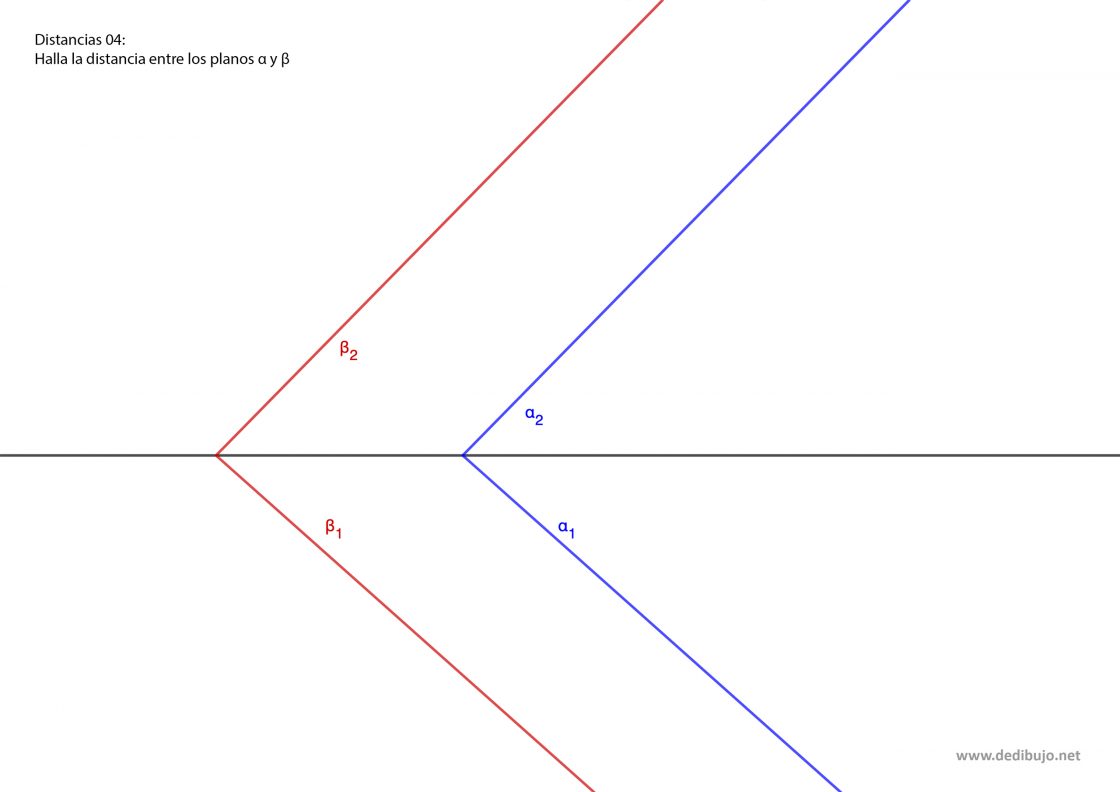
El primer paso es dibujar una recta perpendicular a ambos planos. Yo para hacerlo más sencillo te recomiendo que hagas coincidir la traza de la recta con la traza del plano. De ese modo te ahorras pasos intermedios. Así pues, en este ejemplo marca un punto cualquiera A₂ sobre la traza vertical del plano α.
Para que la recta sea perpendicular, sus proyecciones deben ser perpendiculares a las trazas del plano. Llámalas r₂ y r₁.
Ahora toca determinar los puntos de corte de esa recta que acabas de dibujar con ambos planos. Date cuenta de que el punto A₂ ya es un punto de corte, por lo que solo te falta la intersección con el plano β.
Por cambiar un poco, en este caso traza un plano proyectante horizontal que contenga a la recta r. Los puntos de corte de ese plano con β son B₂ y C₁.
Halla la proyección vertical del punto C₁. Esto lo consigues dibujando una perpendicular a la línea de tierra que pase por C₁ y viendo dónde corta a la misma. Ese punto será C₂, la proyección vertical del punto C.
Une C₂ con B₂ con una línea. Donde esa línea corta a la proyección vertical de la recta r tienes el punto D₂, que es la proyección vertical del punto D. Este es el punto de intersección de la recta r con el plano β.
Traza una perpendicular a la línea de tierra que pase por D₂, donde corta a la proyección horizontal de la recta r tienes el punto D₁, que es la proyección horizontal del punto de intersección.
Para terminar, debes hallar la distancia entre D y A.
1. Sobre la línea que une D₁ con D₂, mide la distancia que hay entre D₁ y la línea de tierra. Esa es la diferencia de alejamientos. A esa distancia puedes llamarla a.
2. Traza una línea perpendicular a la proyección vertical de la recta r y que pase por D₂. Sobre esa perpendicular mide la diferencia de alejamientos. De esa manera tienes el punto E.
3. La distancia existente entre E y A₂ es la distancia que hay entre los dos planos paralelos.

Distancia mínima entre dos rectas oblicuas (perpendicular común)

Cuando hablamos de distancia entre dos rectas, nos referimos a la recta que es perpendicular a ambas. Esta recta se denomina perpendicular común. Date cuenta de que solo puede haber una recta que sea perpendicular a ambas rectas al mismo tiempo (a menos que las rectas sean paralelas). Esta recta determina además la distancia mínima entre ambas rectas.

Cuando una de las rectas es de punta o vertical

Para este tipo de problemas la solución es sencilla, ya que se puede resolver directamente. Te voy a explicar ambos casos. En primer lugar, si una de las dos rectas es vertical, debes hacer lo siguiente:

Traza una recta perpendicular a la proyección horizontal r₁ de la recta oblicua que pase por la traza horizontal s₁ de la recta de punta. El punto de corte D₁ determina la proyección horizontal del segmento que determina la distancia mínima. Por otra parte, la propia traza horizontal de la recta vertical se superpone a la proyección C₁ del punto C que determina el otro extremo del segmento.
La distancia entre D₁ y s₁ (o C₁ si prefieres llamarlo así) te determina la distancia mínima, a la que puedes llamar d.

En caso de que una de las dos rectas sea de punta, entonces tienes la solución sobre la proyección vertical. Para resolverlo haz lo siguiente:

Traza una recta perpendicular a la proyección vertical de la recta oblicua r que pase por la traza vertical de la recta de punta s. Es decir, que pase por s₂.
Donde esa perpendicular corta a r₂ tienes el punto D₂. La distancia entre D₂ y s₂ determina la distancia entre esas dos rectas. Esto significa que ese segmento es la perpendicular común o distancia mínima entre esas rectas.

Cuando las rectas son oblicuas

Este procedimiento es de los más complejos a la hora de calcular distancias, vamos a verlo poco a poco, para que no te pierdas. Básicamente tienes que construir un plano paralelo a una de las rectas, y luego hacer una perpendicular para calcular la distancia. Suponiendo que las rectas iniciales son r y s, sería algo parecido a esto si lo vieras en tres dimensiones.

Si has llegado hasta aquí, entiendo que ya tienes conocimientos básicos del sistema diédrico. Por ese motivo voy a resumir un poco es desarrollo para que no sea tan largo. Tu punto de partida será algo parecido a lo que ves a continuación:

Puedes imprimir esta imagen para practicar el ejercicio

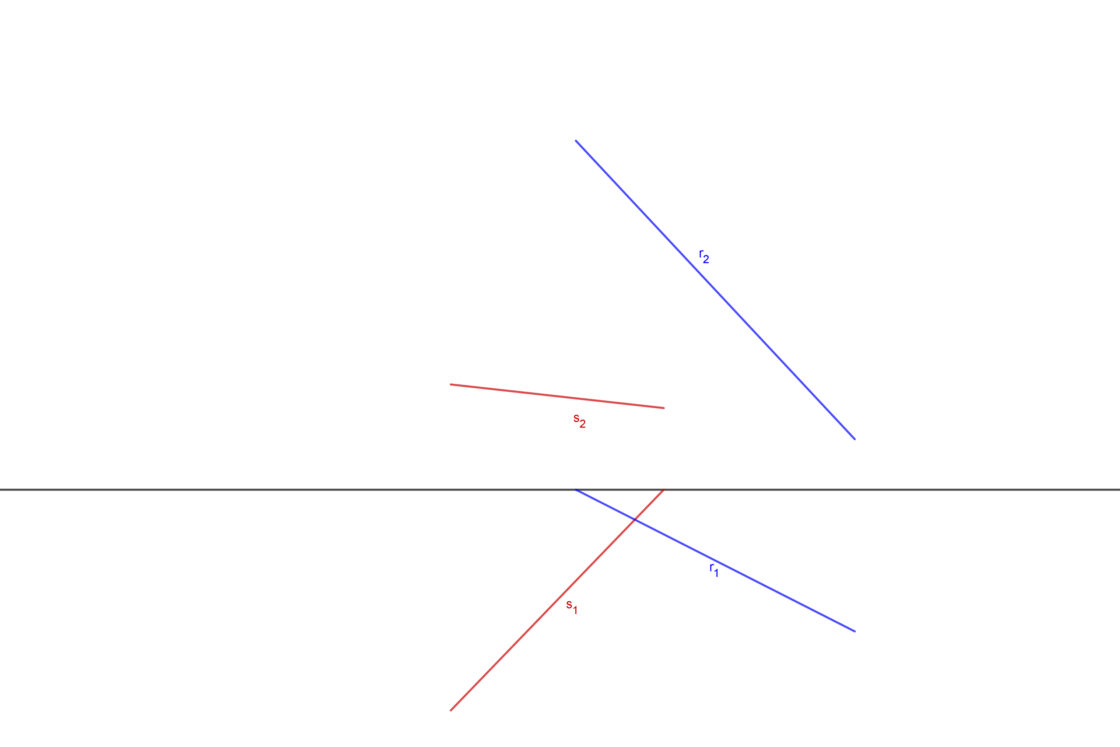
Lo primero es determinar un plano paralelo a r y que contenga a s. Para ello dibuja una recta paralela a r y que corte a s en un punto cualquiera. A esa recta puedes llamarla t y al punto de corte A.
Ahora dibuja las trazas del plano que forman s y t. Ese plano puedes llamarlo α.
Dibuja una recta perpendicular al plano α y que pase por un punto cualquiera de r. Ese punto cualquiera llámalo B y a ésta recta perpendicular llámala n.
Calcula la intersección de n con el plano α. El punto de intersección puedes llamarlo C.
La distancia entre C y B es equivalente a la distancia entre ambas rectas.

Ayúdame a mejorar esta entrada

¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti. Gracias de antemano por dejar tu comentario un poco más abajo.

«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.