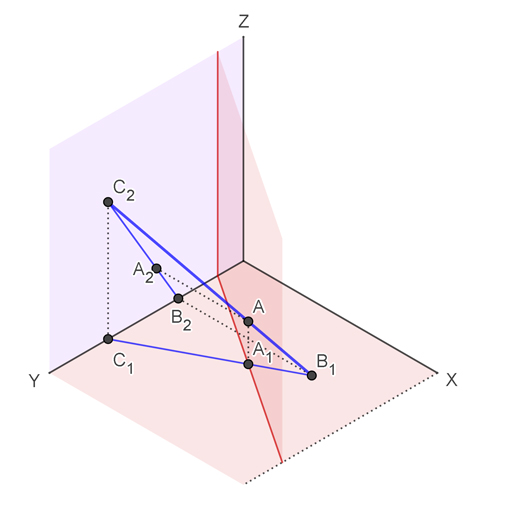
Estos tipos de intersecciones son casos bastante particulares en lo que a la intersección de rectas y planos en sistema diédrico se refiere. Algunos de ellos son muy útiles a la hora de resolver otros ejercicios más complejos, por lo que es recomendable saber solucionarlos correctamente.
Intersección de una recta con un plano proyectante horizontal
En este caso, la intersección de la traza horizontal del plano coincide con la proyección horizontal del punto de intersección, al que en este caso he llamado A1. Para hallar la proyección vertical del punto de intersección solo tienes que levantar una perpendicular a la línea de corte que pase por A1, donde esa perpendicular corta a la proyección vertical de la recta tienes el punto A2, que es la proyección vertical del punto de intersección.
Intersección de una recta de punta con un plano cualquiera
La proyección vertical del punto de intersección coincide con la traza de la recta con el plano vertical (esto es muy obvio). Para hallar la proyección horizontal del punto de intersección debes realizar una recta horizontal contenida en el plano.
- Empieza por dibujar una recta paralela a la línea de tierra que pase por A2. Donde esa recta corta a la traza vertical del plano tienes el punto B2.
- Traza una perpendicular a la línea de tierra que pase por B2. Donde esa perpendicular corta a la línea de tierra tienes el punto B1.
- Dibuja una recta paralela a la traza horizontal del plano que pase por B1. Donde esa paralela corta a la proyección horizontal de la recta de punta tienes el punto A1. Ese punto es la proyección horizontal del punto de intersección.
Aquí abajo puedes ver como se resolvería en diédrico.
Intersección de una recta vertical con un plano oblicuo
Como puedes ver, este ejercicio es muy similar al anterior. La diferencia radica en que la proyección horizontal del punto de corte coincide con la traza horizontal de la recta. Para hallar la proyección horizontal del punto de intersección puedes realizar una recta horizontal o frontal contenida en el plano.
- Empieza por dibujar una recta paralela a la traza horizontal del plano que pase por A1. Donde esa recta corta a la línea de tierra tienes el punto B1.
- Traza una perpendicular a la línea de tierra que pase por B1. Donde esa perpendicular corta a la traza vertical del plano tienes el punto B2.
- Dibuja una recta paralela a la línea de tierra que pase por B2. Donde esa paralela corta a la proyección vertical de la recta vertical tienes el punto A1. Ese punto es la proyección vertical del punto de intersección.
Intersección de una recta con el primer bisector
Date cuenta de que al encontrase la intersección sobre el primer bisector, la distancia de las proyecciones del punto a la línea de tierra deben ser iguales. Por lo tanto, la forma más fácil de hallar el punto de intersección es dibujar una recta simétrica a una de las dos proyecciones de la recta respecto de la línea de tierra. Si este proceso te resulta confuso, una forma bastante fácil de resolverlo es utilizando la tercera proyección sobre el plano de perfil.
En este ejemplo, puedes ver que he dibujado una recta simétrica a la que forman A2 y B2 respecto de la línea de tierra. Donde esa recta corta a la proyección horizontal de la recta tienes el punto C, que es el punto de intersección de la recta con el primer bisector.
Intersección de una recta con el segundo bisector
Este tipo de ejercicios no es demasiado frecuente, ya que no es usual tener que hallar intersecciones más allá del primer diedro. Seamos sinceros, cualquier tipo de problema referente a los otros diedros se podría solucionar cambiando el centro de los ejes de tal manera que todos los puntos de las figuras a representar queden en el primer diedro. No obstante, déjame que te explique como solucionarlo (por si acaso).
Si te das cuenta, este ejercicio es parecido al anterior. La principal diferencia radica en que al cortar fuera del primer diedro (el segundo o el cuarto), las proyecciones del punto de corte coincidirán. Si corta en el segundo diedro (detrás) coincidirán en el plano vertical. Por otra parte, si corta en el cuarto diedro (debajo) las proyecciones coincidirán en el plano horizontal. En cualquier caso, date cuenta de que al tratarse de un punto de la recta, y además ser sus proyecciones coincidentes, por definición el punto será la intersección de ambas proyecciones. Da igual si se corta con el segundo bisector en el segundo o cuarto diedro. En caso de cortar en el cuarto diedro, entonces las proyecciones estarán debajo de la línea de tierra.
Intersección de una recta horizontal con un plano oblicuo
Tanto este ejercicio, como el siguiente, se podrían solucionar con un plano proyectante auxiliar. El problema de este tipo de ejercicios es que lo plantean de tal manera que el plano proyectante cortaría a las trazas del plano fuera del espacio de trabajo, para confundirte. En realidad, este caso es bastante sencillo, ya que puedes utilizar la proyección vertical de la recta como proyección vertical de una recta auxiliar que te ayudará a solucionar el problema. Donde la recta auxiliar corta a la recta horizontal tienes la solución.
Intersección de una recta frontal con un plano oblicuo
Este problema se soluciona igual que en el ejercicio anterior, lo que te recomiendo es que utilices la proyección horizontal de la recta que te proporcionan. De esa manera te ahorras parte del trabajo.
Intersección de una recta paralela a la línea de tierra con un plano oblicuo
Claro, ves este problema y lo primero que te planteas es «¿y como hago yo un plano proyectante a ésto?». Pues la respuesta es muy sencilla… Se trata de un plano frontal u horizontal. Aquí abajo yo lo he solucionado con un plano frontal, aunque también podría haber usado un plano horizontal. Como puedes ver, primero he hallado la traza horizontal de la intersección de ambos planos, y con ella he podido hallar la intersección con la recta haciendo una recta paralela a la traza vertical del plano oblicuo.
Intersección de una recta paralela al plano de perfil con un plano oblicuo
Para resolver este problema, lo más sencillo es recurrir a la tercera proyección.
