Definición de triángulo
Un triángulo es una figura plana delimitada por tres rectas que se cortan dos a dos. Está compuesta por tres lados y tres ángulos. Para definirlo debemos nombrar sus lados y ángulos. Una forma correcta de realizar la nomenclatura de los triángulos sería la siguiente:
- Los ángulos se nombran con letras mayúsculas
- Los lados se designan con letras minúsculas, correspondiéndose con las que tienen los ángulos opuestos.
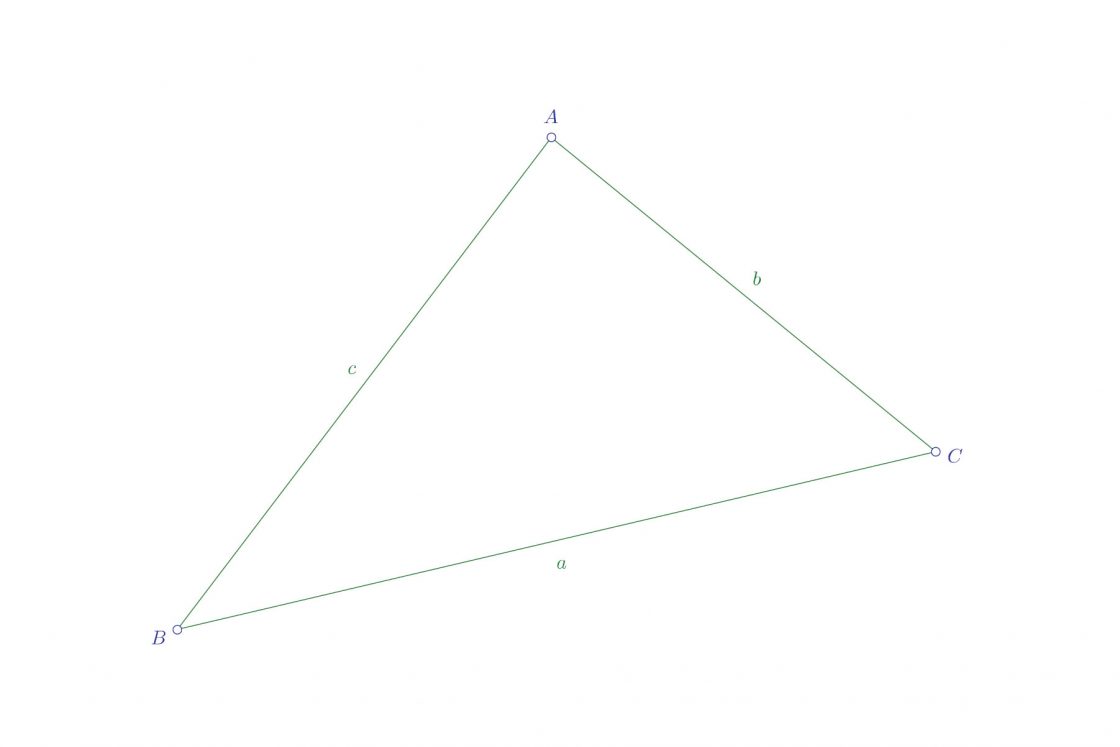
Como podéis ver, el ángulo C se corresponde con el lado opuesto c, y así sucesivamente con todos los lados del triángulo.
Propiedades de los triángulos
Una propiedad muy interesante de los triángulos y que nos ayudará a construir y comprender polígonos más complejos es que la suma de sus ángulos es siempre 180º
Relacionado con sus lados, hay un par de propiedades que también soy muy interesantes, a saber:
- Cada lado es siempre menor que la suma de sus lados opuestos.
- Cada lado es siempre mayor que la diferencia de sus lados opuestos.
Si no te lo crees, lo puedes comprobar aquí abajo moviendo los puntos A, B y C.
Clasificación y tipos de los triángulos
Los triángulos se pueden clasificar en función de sus lados o sus ángulos. En el primer caso, dependiendo de las relaciones existentes entre sus lados los podremos clasificar en:
- Equiláteros: Cuando sus tres lados son iguales. Se da además la propiedad de que al cumplirse esta condición, sus tres ángulos también serán iguales.
- Isósceles: Cuando dos de sus lados son iguales. De forma similar a lo que pasaba con el caso anterior, en esta ocasión se cumple que los ángulos opuestos a los lados iguales también son iguales.
- Escaleno. En este caso, sus tres lados son diferentes, y también lo son sus ángulos.
En función de sus ángulos, podemos encontrar los siguientes tipos de triángulo:
- Acutángulos: Cuando sus tres ángulos son agudos (es decir, menores de 90 grados)
- Rectángulos: Cuando uno de sus ángulos mide 90 grados, es decir se trata de un ángulo recto. Se cumple la propiedad de que siempre la suma de los dos lados opuestos al recto es de 90 grados.
- Obtusángulo: Cuando uno de sus lados es mayor de 90 grados, es decir, obtuso.
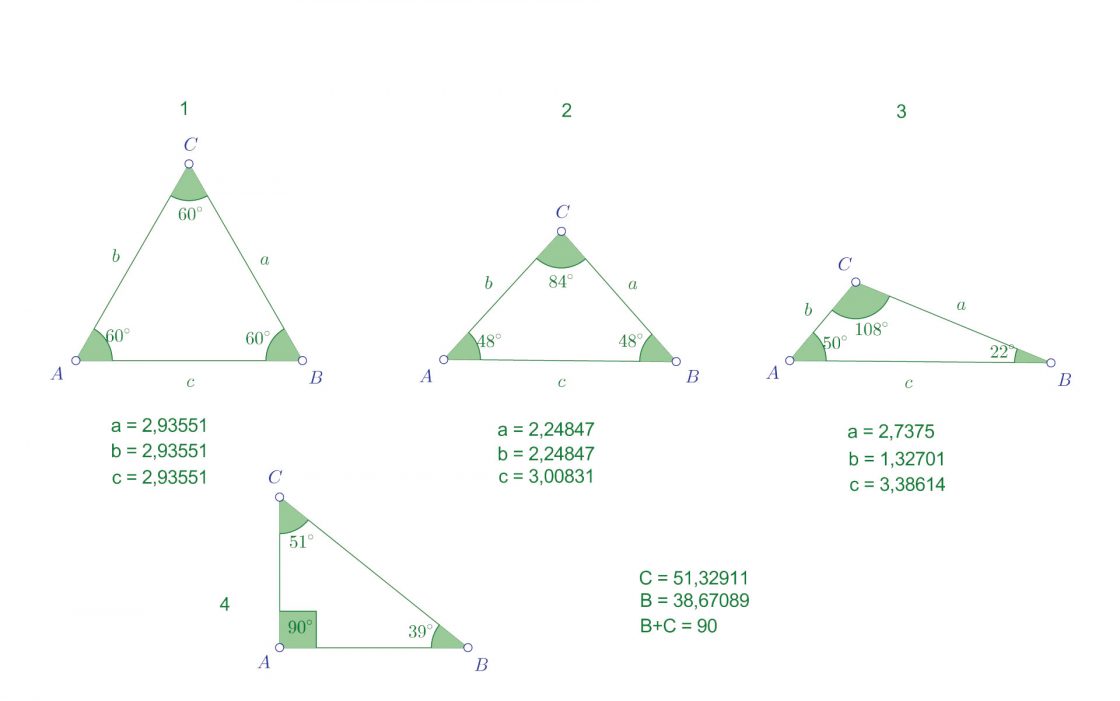
En la siguiente imagen podéis ver los diferentes tipos de triángulos según su clasificación por sus lados y ángulos. El número uno sería un triángulo equilátero. El número dos sería al mismo tiempo isósceles y acutángulo, ya que tiene dos lados iguales y todos sus ángulos son menores de 90 grados. El tres sería al mismo tiempo obtusángulo, ya que tiene un ángulo mayor de 90 grados, y escaleno, ya que todos sus lados son distintos.
Líneas notables en el triángulo
Las líneas notables del triángulo son:
- Mediana: Es la línea que va desde un vértice a la mitad del lado opuesto.
- Mediatriz: Es la línea perpendicular a un lado que pasa por la mitad del mismo.
- Bisectriz: Es la línea que divide un ángulo del triángulo en dos partes iguales.
- Altura: Es la línea perpendicular a un lado que pasa por el vértice opuesto.
Aquí abajo puedes mover los puntos A, B y C para modificar el triángulo y ver como se comportan los distintos tipos de líneas notables del triángulo.
La mediana parte la altura por la mitad
Una propiedad interesante de la mediana, y que se suele usar en la resolución de algunos problemas de triángulos es que al mismo tiempo que parte el lado en la mitad, también parte la altura del triángulo en la mitad. Aquí abajo tienes una demostración práctica. Puedes mover los puntos A y C, la mediana y la altura se ajustarán solas. Podrás comprobar como al mismo tiempo que partes la mediana, si realizas una paralela a la base por el punto medio del lado c, también obtendrás la mitad de la altura.
La altura no puede ser mayor que la mediana
Esta es otra propiedad interesante que se suele ver a la hora de plantear ejercicios de triángulos. Si en algún momento te dan un valor para una altura que es mayor que el de la mediana, te están poniendo a prueba. Di que hay un error en el enunciado. ¿No te lo crees? Puedes comprobarlo moviendo los puntos A y C aquí abajo. Como mucho, podrían llegar a ser iguales.
También te puede interesar…
29 octubre, 2020

Trapecios y trapezoides
23 octubre, 2020

Cuadriláteros y paralelogramos, definición y clasificación
15 noviembre, 2019
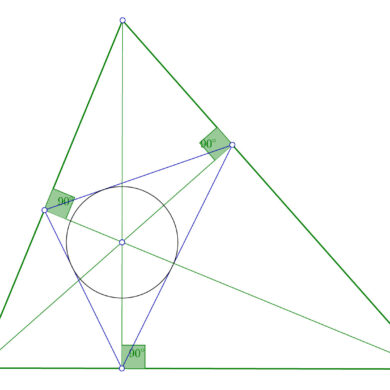
Baricentro, ortocentro, circuncentro, incentro ⚠️ Propiedades y definición
Como siempre espero que hayáis encontrado interesantes estos recursos didácticos. Recordad que para construir triángulos necesitaréis escuadra y cartabón y conocimientos básicos sobre la contrucción de perpendiculares y otras rectas notables. Y si queréis saber más sobre los triángulos, podéis continuar con este tema visitando la explicación del baricentro, ortocentro, incentro y circuncentro, los puntos notables de los triángulos.
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti. Gracias de antemano por dejar tu comentario un poco más abajo.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
