¿No te has preguntado nunca por qué las cosas son como son? Ves algún tipo de explicación y te dices: «Vale, se como se hace, pero… ¿Por qué se hace así y no de otra manera?». Hace tiempo leí que las personas que se hacen este tipo de preguntas suelen tener una mente inquisitiva que demuestra una capacidad intelectual más alta de la media. Algunas de estas personas se dedican a la investigación y son las que hacen que el mundo sea un lugar mejor. Hoy quiero dedicar esta entrada a todas esas personas.
Esta entrada es tan solo para explicar el que considero que es el problema más importante referente a tangencias de primero de bachillerato. Como hallar las rectas tangentes a una circunferencia que pasan por un punto exterior a la misma. Hay muchas formas de explicarlo, tanto matemática como geométricamente. A continuación explicaré algunas de ellas, las que creo que son más relevantes.
Justificación mediante las propiedades de las tangencias
Empiezo por esta porque creo que es la más importante. Si no las conoces, te recomiendo visitar el enlace donde hablo de las propiedades de las tangencias, porque creo que son muy importantes. Las dos que hacen referencia a este problema son las siguientes:
- Una circunferencia tangente a una recta siempre tendrá su centro sobre la perpendicular a dicha recta por el punto de tangencia.
- Una circunferencia a dos rectas siempre tendrá su centro sobre la mediatriz del ángulo que formen dichas rectas.
La primera propiedad se explica fácil porque una circunferencia tangente a una recta solo comparte un punto con la misma. Si comparte dos, ya no es tangente, sino secante. En el caso de la segunda propiedad, se puede explicar pensando que es una construcción simétrica.
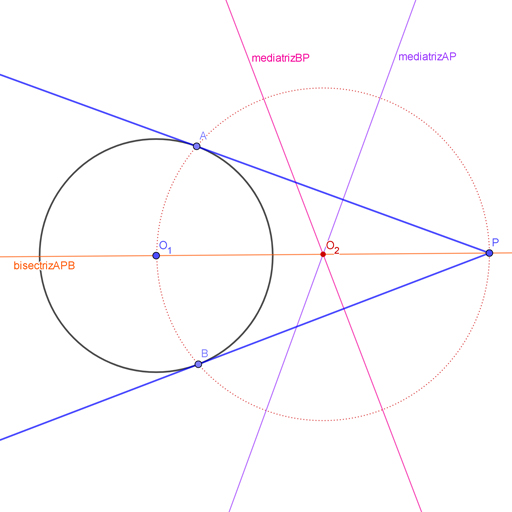
A continuación te propongo un juego. Puedes mover los puntos P, A y B para modificar las rectas. También puedes mover el punto O1 para mover el centro de la circunferencia. Trata de mover los puntos A y B para que las rectas sean tangentes. Al hacerlo fíjate en lo que pasa con las perpendiculares, con la bisectriz y con el centro O2, que es el centro de la circunferencia que pasa por A. B y P. ¿Dónde acaba O2? Justo a medio camino entre O1 y P.
Explicación por circunferencias
Supongo que sabes como dibujar una circunferencia que pase por tres puntos. Si no, te lo explico que es muy sencillo. Imagina una circunferencia que pase por A, P y B. La forma de determinar el centro es hacer la mediatriz del segmento que formen dos de esos puntos, por ejemplo AP y BP. Donde esos puntos se cortan tienes el centro. Ahora bien, como te comentaba antes, Si una recta es tangente, entonces solo toca a la circunferencia en un punto. A continuación lo puedes comprobar. Como antes puedes mover los puntos A y B para modificar las rectas. También puedes mover el punto O1 para cambiar la posición de la circunferencia. Por supuesto también puedes mover P.
Trata de mover los puntos A y B para que se encuentren sobre los puntos de tangencia. ¿Qué pasa con las mediatrices de AP y de BP? ¿Dónde acaba el centro de la circunferencia que pasa por A, P y B? De nuevo se repite la situación de antes.
Explicación por potencias
Este tal vez sea el método más complejo para explicar porqué T1 y T2 son los puntos de tangencia. Se explica mediante el concepto de potencia, que se suele explicar en segundo de bachillerato. No voy a entrar en detalle, si quieres saber un poco más sobre este tema, te recomiendo visitar la entrada donde hablo de las propiedades de las potencias y su aplicación en el tema de las tangencias. Por resumirlo mucho, si dibujas líneas que pasen por P y que corten a la circunferencia, el resultado de multiplicar los segmentos resultantes entre P y los puntos de corte es siempre constante. Por ejemplo, si multiplicas PA por PC, el valor siempre será constante. Partiendo de la base de que Si las rectas son tangentes A y C están en el mismo sitio, y por tanto PA y PC son iguales, entonces la distancia entre P y los puntos de tangencia debe ser la raíz cuadrada de PA por PC.
Como te digo, este concepto es un poco complejo. De todas formas, aquí abajo te dejo una aplicación para que lo compruebes por ti mismo. Puedes mover los puntos A y B para mover las rectas. También el punto P y para terminar el centro de la circunferencia O1 para mover el centro de la circunferencia. Te recomiendo ponerlo a pantalla completa para verlo mejor.
