Dibujar una elipse a partir de cinco puntos

Este podría parecer un problema típico cuando se aprenden curvas cónicas y elipses, pero no es así. Se trata de un complejo problema de homología. Para dibujar una elipse a partir de cinco puntos lo que debes recordar es que la figura homóloga de una circunferencia es un círculo. También debes saber que si esa circunferencia corta al eje, entonces tendrá dos puntos homólogos de si mismos. Es decir, su representación en la elipse no cambiará. A continuación te expongo dos maneras distintas de resolverlo, y como colofón, como hallar los ejes de una elipse cuando conocemos el eje de homología, el centro de homología, la circunferencia homóloga y una recta límite.

Dibujar una elipse a partir de cinco puntos

Unimos los puntos mediante líneas, determinando un polígono. Si estos puntos encierran un pentágono cóncavo, entonces la figura resultante será una elipse. A cada uno de los puntos llámalos V₁, V₂, V₃, V₄ y V₅, que son los vértices del pentágono irregular que define la elipse. Las líneas que unen esos vértices son los lados del pentágono que puedes llamar L₁, L₂, L₃, L₄ y L₅.
Prolonga L₁ y L₄, donde esas rectas se cortan tienes el punto A.
A continuación prolonga L₂ y L₅, donde esas rectas se cortan tienes el punto B.
Dibuja la línea que pasa por A y B. Esa línea que acabas de dibujar es la Recta de Pascal, en este ejemplo la he llamado RPascal, para que puedas identificarla.
Ahora prolonga L₃ hasta cortar a esa línea. El punto de corte será C.
Lo siguiente que debes hacer es dibujar la línea que pasa por C y V₁. Esa es la recta tangente a la elipse por el punto V₁. Para que puedas identificarla la he llamado RTangente.
Para poder continuar vamos a considerar que V₁ es el centro de la homología.
Continúa dibujando una perpendicular a RTangente que pase por V₁. Marca cualquier punto de esa perpendicular como O₁, y dibuja una circunferencia de centro O₁ y radio hasta V₁.
El siguiente paso es hallar el eje de homología. Para ello vamos a hallar los puntos homólogos de algunos que conozcamos. Donde la prolongación de L₁ corta a esa circunferencia que acabas de dibujar tienes V₂‘, homólogo de V₂. Donde la prolongación de L₅ corta a la circunferencia tienes V₅‘, que es el homólogo de V₅. Como necesitas otro punto más, dibuja una línea que pase por V₃ y V₁. Donde esa línea corta a la circunferencia tienes el punto V₃‘, homólogo de V₃.
Ahora con todas esas líneas vamos a hallar el eje. Recuerda que dos rectas homólogas siempre se cortan en el eje, así pues, dibuja las rectas que pasan por V3 y V5, y comprueba donde se cortan con la recta que pasa por V3′ y V5′. Ese punto de corte llámalo D.
Repite el proceso trazando líneas que pasen por V2 y V3 (es la prolongación del lado L2) y que pasen por V2′ y V3′. Esas dos líneas se cortan en el punto E.
Tanto D como E son homólogos de si mismos. Por tanto se encuentran sobre el eje de homología. Es decir, si trazas la recta que pasa por D y E ya tienes dibujado el eje de homología.
Una vez que tienes el centro de homología y el eje, puedes resolver el problema de la forma habitual que se utiliza para dibujar la figura homóloga de un círculo.
Si quieres hallar los ejes de la elipse, necesitarás una recta límite. Para ello dibuja una recta paralela a la recta que pasa por V3 y V5 que pase por V1. Donde esa recta corta a la que pasa por V3′ y V5′ tienes el punto F, que pertenece a la recta límite, que llamaremos RLimite. Trazando una recta paralela al eje que pase por F ya tienes la recta límite.

Continuación del ejercicio anterior: Hallar los ejes

Llegados al punto anterior, he borrado todo aquello que no necesito para terminar el ejercicio. Me he quedado con la circunferencia, el eje, la recta tangente y la recta límite. El punto de partida será algo similar a esto.

Marca el punto de intersección de RTangente con Rlimite. A ese punto llámalo A.
Dibuja una circunferencia de centro A y radio hasta V₁. Los puntos donde esa circunferencia corta a Rlimite llámalos B y C.
Ahora dibuja una recta tangente a la circunferencia que pase por B. El punto de tangencia será T₁. Une el punto de tangencia con C.
A continuación dibuja una recta tangente a la circunferencia que pase por C. El punto de tangencia lo llamaremos T₂. Dibuja la recta que pasa por T₂ y B.
El lugar donde se cortan estas dos rectas llámalo O₂. El punto O₂ es el homólogo del centro de la elipse.
Los puntos donde estas rectas cortan a la circunferencia llámalos D y E. Estos puntos, junto con los puntos de tangencia T₁ y T₂ son homólogos de los vértices que marcan los ejes de la elipse.
Ahora dibuja una recta cualquiera que pase por T₂. Los puntos donde corta al eje y a la recta límite llámalos L y L’.
Marca el segmento que forman V₁ y L. Luego haz una paralela a ese segmento que pase por L’.
Une T₂ con V₁, donde corta a la recta que dibujaste en el paso anterior tienes el punto T₂‘, que determina uno de los extremos de uno de los ejes.
Para hallar D’ tienes que repetir el proceso. Dibuja una línea cualquiera que pase por D y que corte a la recta límite en M y al eje en M’. Une V₁ con M. Traza una paralela a ese segmento que pase por M’. Donde esa recta corta a la que pasa por D y V₁ te está marcando el punto D’.
El segmento que forman D y D’ te determina uno de los ejes de la elipse.
Ahora dibuja una recta cualquiera que pase por T₁, esa recta corta a la recta límite en K y al eje en K’. Une V₁ con K. Dibuja una paralela a esa recta que pase por K’. Donde esa recta corta a la que pasa por T₁ y V₁ tienes el punto T₁‘.
Vamos a determinar el último punto de los ejes. Dibuja una recta cualquiera que pase por T₂. Esta recta corta al eje en el punto N y a la recta límite en el punto N’. Une N con V₁. Dibuja una recta paralela a ese segmento que pase por N’. Donde esa recta corta a la que pasa por T₂ y V₁ tienes el punto T₂‘, homólogo de T₂.
El segmento T₂‘ y T₁‘ determina el otro eje de la elipse.

Como trazar una elipse a partir de cinco puntos

Este procedimiento lo tengo aquí para que no se me olvide repasarlo. Me lo he encontrado en una página web, pero no sale bien el resultado. Tengo que repasar todos los pasos uno por uno porque me temo que hay alguno que está equivocado.

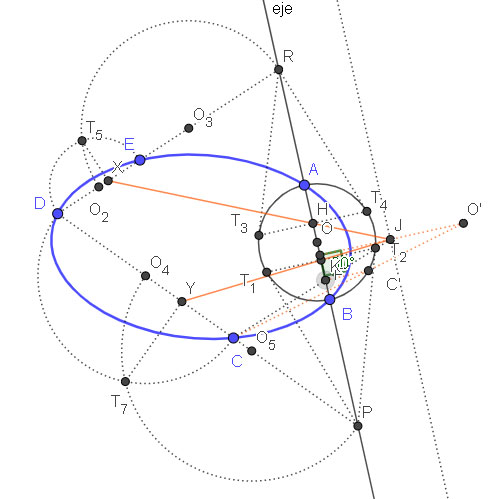
Selecciona dos puntos de la elipse que conoces. Para este ejemplo toma como referencia A y B. Vamos a considerar que estos puntos están sobre el eje de homología, y que por tanto son homólogos de si mismos.
Halla el punto medio entre A y B, al que llamaremos O.
Dibuja una circunferencia de centro O y radio hasta A.
Prolonga la recta que une A y B, ya que esta será el eje de homología.
Ahora dibuja líneas que pasen por los otros puntos de la elipse que conoces. Una por C y D, y otra por D y E. Donde esas rectas cortan al eje tienes los puntos P y R, que también son homólogos de si mismos.
Halla la recta polar del punto P respecto a la circunferencia de centro O. Para ello tienes que hallar los puntos de tangencia de la circunferencia de centro O. Esos puntos son T₁ y T₂. Une esos puntos con un segmento, donde esos puntos cortan al eje tienes el punto F.
A continuación tienes que hallar la polar de R respecto a la circunferencia de centro O. Para ello tienes que hallar los puntos de tangencia de las rectas que pasan por R con la circunferencia de centro O. Esos puntos serán T₃ y T₄. Si unes esos puntos con una línea, donde cortan al eje tienes el punto H.
El siguiente paso es hallar los puntos armónicos conjugados tanto de F como de H. Te lo explico poco a poco para no liar más de la cuenta este ejercicio.
Halla el punto medio del segmento DE, que puedes llamar O₂. Dibuja la circunferencia (en realidad solo necesitas media) y luego halla los puntos de tangencia de R respecto a esta circunferencia, que serían T₅ y T₆ (solo he marcado T₅ y he hecho una perpendicular para evitar líneas innecesarias). El punto donde corta a la recta que pasa por D, E y R es X. Ese punto es el polo de la circunferencia de centro O₂ respecto de R. Ese punto es el conjugado armónico de H.
Ahora marca el punto medio de C y D. Ese punto es O₄. Dibuja la circunferencia de centro O₄ y radio hasta C. A continuación debes hallar los puntos de tangencia de las rectas que pasan por P y son tangentes a esa circunferencia. Esos puntos serían T₇ y T₈ (como antes, solo he marcado uno y he hecho perpendicular para abreviar). Si unes esos puntos obtienes Y, que es el polo de esa circunferencia respecto a P.
Lo siguiente que debes hacer es dibujar las líneas que unen Y con F por un lado y X con H por el otro. Donde ambas rectas se cortan tienes el punto J. Este punto se encuentra sobre la perpendicular que une el centro de homología O con el eje.
Para hallar el centro de homología necesitas un par de puntos homólogos. En este ejemplo vas a hallar el homólogo de C. Para ello traza la línea que une C con J y mira donde corta al eje. Ese punto llámalo K. Ahora dibuja una perpendicular al eje que pase por K. Donde esa perpendicular corta a la circunferencia de centro O tienes C’.
Une C con C’ con una línea y prolóngala hasta cortar a la perpendicular al eje que pasa por J. Ese punto de corte es el centro de homología O’.
Llegados a este punto puedes resolverlo usando la forma habitual para dibujar la figura homóloga a un círculo.

Aquí abajo tienes una aplicación interactiva para que veas como funciona. Te recomiendo ponerlo a pantalla completa y hacer zoom sobre cada zona, ya que son muchos puntos y están todos muy juntos.

Hallar los ejes de la elipse conociendo el eje, una recta límite, el centro de homología y la circunferencia homóloga

Los datos que conoces serían la circunferencia inicial, el centro de homología y el eje de homología. Si no te proporcionan la recta límite, te deben proporcionar un par de puntos homólogos para resolver el ejercicio. Si no sabes que son y como se hallan las rectas límite, te recomiendo visitar el enlace donde explico como hallar rectas límite en homología. Yo voy a continuar con el primer ejercicio, pero borrando todos los pasos intermedios que ya realicé para que el ejercicio quede más claro. Así pues, el punto de partida es algo parecido a ésto.

Empieza hallando la recta polar del centro de homología O’ respecto de la circunferencia de centro O. Es decir, hallas los puntos de tangencia de las rectas que pasan por O’ con la circunferencia. Esos puntos llámalos T1 y T2.
Si unes T1 y T2 con una línea, donde esa línea corta al segmento que forman O y O’ tienes el punto F, polo de la circunferencia con el centro de homología.
Ahora halla el punto medio de O’ y F, al que puedes llamar H.
Dibuja una perpendicular al segmento que forman O y O’ que pase por por H y mira donde corta a la recta límite. Ese punto de corte llámalo I.
Con centro en I y radio hasta O’ dibuja una circunferencia que corta a la recta límite en los puntos J y K.
Ahora dibuja líneas que unan J y K con el centro O de la circunferencia. Donde esas líneas cortan a la circunferencia que dibujaste en el paso anterior (la de centro I) tienes los puntos de corte L y M.
El siguiente paso es dibujar una línea que pase por K y L hasta cortar a la circunferencia. Los dos puntos de corte con la circunferencia son N y P.
A continuación dibuja una recta que pase por J y M. Donde esa recta corta a la circunferencia tienes los puntos R y S.
Los segmentos RS y NP son las líneas homólogas a los ejes de la elipse. Al punto donde se cortan llámalo T. El punto T es el punto homólogo al centro de la elipse.