Potencia, eje radical y centro radical

Hay multitud de problemas referentes a circunferencias tangentes que se pueden solucionar empleando diversos usos del concepto de potencia. En esta ocasión vamos a ver las más comunes. Pero lo primero de todo…

¿Qué es el concepto de potencia?

El concepto de potencia es una constante de un punto respecto a una circunferencia. Si trazamos una línea cualquiera que parte del punto P y que corta a la circunferencia en dos puntos distintos R y S, esta constante será igual a PR multiplicado por PS. Aquí abajo os pongo un vídeo muy breve donde os lo demuestro con números para que lo veáis más claro.

Por si lo no te lo crees, lo puedes comprobar aquí abajo moviendo P, R y O.

Potencia de un punto interior a la circunferencia

La forma de calcular la potencia de un punto interior a la circunferencia se realiza trazando rectas secantes que pasen por ese punto. En el siguiente ejemplo puedes ver que se han creado dos segmentos para cada recta. La potencia en este caso se calcula multiplicando entre si los segmentos que se encuentran en la misma cuerda de la circunferencia. La única diferencia es que al tratarse de un punto interior, la potencia se considera negativa.

Segmento representativo de potencia

A la hora de hablar del segmento representativo de potencia nos estamos refiriendo a aquel que multiplicado por si mismo nos devuelve el valor de la potencia. En el caso de un punto exterior es fácil, ya que sólo tienes que hallar las rectas tangentes a la circunferencia y que pasan por P. Si quieres comprobarlo, puedes verificarlo un poco más arriba.

El el caso de tratarse de un punto interior, la cosa cambia ligeramente. Para ello debes trazar el radio que contiene a P, y luego hacer una perpendicular a dicho radio que pasa por P. El segmento que tienes entre P y la circunferencia es el segmento representativo de potencia. Aquí abajo puedes mover los puntos A y P y verás que siempre se cumple. Ten en cuenta que en este caso el valor es negativo porque es un punto interior.

Eje radical de dos circunferencias

Ahora que ya sabes lo que es el concepto de potencia, te voy a explicar otro concepto que está muy relacionado; el eje radical. Se define como «El lugar geométrico de los puntos del plano que tienen una misma potencia respecto de dos circunferencias, representándose como una recta.» Y así es, si calcularas todos los puntos que tienen la misma potencia respecto de dos circunferencias, estos formarían una línea. Se dan tres casos particulares; cuando las circunferencias están alejadas, cuando son tangentes y cuando se cortan. En el caso de que se corten, la línea pasará por los puntos de corte. Si son tangentes entre si, el eje radical será la recta tangente a ambos. Hay varias maneras de hallar el eje, a continuación te explicaré las mas comunes.

Método 1, mediante una circunferencia secante

En mi opinión, este es el método más sencillo. Los demás los pongo solo a modo de complemento, aunque no los explico en clase para no complicarle la vida a mis alumnos, y todavía no he visto ningún examen de la EVAU en el que exijan usar uno u otro, y que no se pueda resolver con éste método. Así pues, tu punto de partida será semejante a esto:

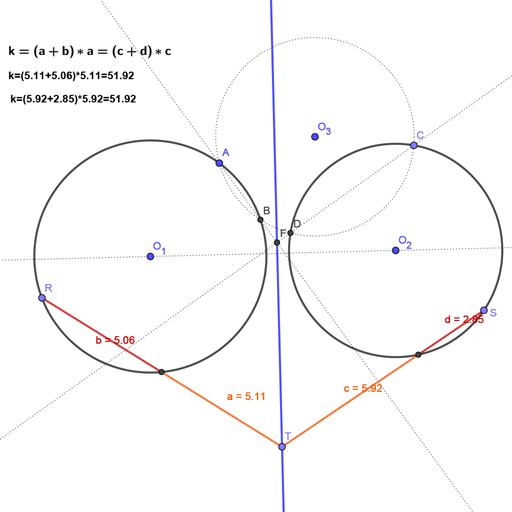
Dibuja una circunferencia cualquiera, con centro cualquiera, y radio cualquiera, que corte a ambas circunferencias. Aquí abajo es la circunferencia de centro O₃, que corta a las circunferencias iniciales en los puntos A, B, C y D.
Dibuja la línea que pasa por A y B.
Ahora traza la recta que pasa por C y D.
El punto donde se cortan las dos rectas anteriores puedes llamarlo F.
pA continuación dibuja la línea que une los centros de las dos circunferencias iniciales, O₁ y O₂
Haz una recta perpendicular a esa recta, que pase por el punto F que habías hallado antes. Esa recta es el eje radical.

Puedes mover los puntos R, S y T para verificar que la potencia de cualquier punto de esa recta es siempre constante respecto a cualquier punto de cualquiera de las dos circunferencias. Fíjate en las posiciones particulares del eje radical moviendo el centro O₂.

Si las circunferencias son tangentes, el eje radical es una recta tangente a ambas.
Cuando son secantes, el eje radical pasará por los puntos de corte de ambas circunferencias.
En caso de que una circunferencia inscriba a la otra, se calcula exactamente igual, y el eje radical se encontrará fuera de ambas, como en cualquier otra situación.

Método 2, mediante rectas tangentes

Este método consiste en dibujar las rectas tangentes a ambas circunferencias. Después solo queda hallar los puntos medios entre los puntos de tangencia y unirlos con una recta. Esa recta es el eje radical de ambas circunferencias. Si no recuerdas como dibujar las tangentes, te recomiendo visitar la entrada donde explico como hallar las tangentes más básicas.

Método 3: Mediante arcos de circunferencia

Aquí tienes una tercera manera de hallar el eje radical de dos circunferencias. Te lo explico brevemente, es muy sencillo.

Como en problemas anteriores, dibuja una línea auxiliar que una O₁ con O₂.
Dibuja un radio cualquiera de la primera circunferencia, la de centro O₁ en este caso. Al punto de corte con la circunferencia llámalo A.
Dibuja una perpendicular a ese radio (es una tangente), y lleva una medida cualquiera sobre ella, hallando el punto B.
Con centro en O₁ y radio hasta B, dibuja un arco de circunferencia.
Continúa haciendo lo mismo, pero con la otra circunferencia. Es decir, dibuja un radio cualquiera de la circunferencia de centro O₂. El punto de corte con la circunferencia es C.
Ahora traza una perpendicular al radio O₂C que pase por C.
Sobre esa perpendicular mide la longitud del segmento AB, de esa manera obtienes el punto D.
Dibuja un arco con centro O₂ y radio D. Ese arco corta con el que dibujaste antes en el punto E.
El eje radical de ambas circunferencias será la recta perpendicular a la línea que une O₁ y O₂ y que pasa por E.

Eje radical de un punto y una circunferencia

Del mismo modo que puedes hallar el eje radical de dos circunferencias, puedes hallar el eje radical de un punto y una circunferencia. Una forma muy gráfica de visualizar esto sería imaginar que una de las dos circunferencias es tan pequeña que parece un punto. ¿Cómo sería una circunferencia de radio cero? Pues un punto. ¿Cómo solucionar éste problema? Tu punto de partida se debe parecer a esto:

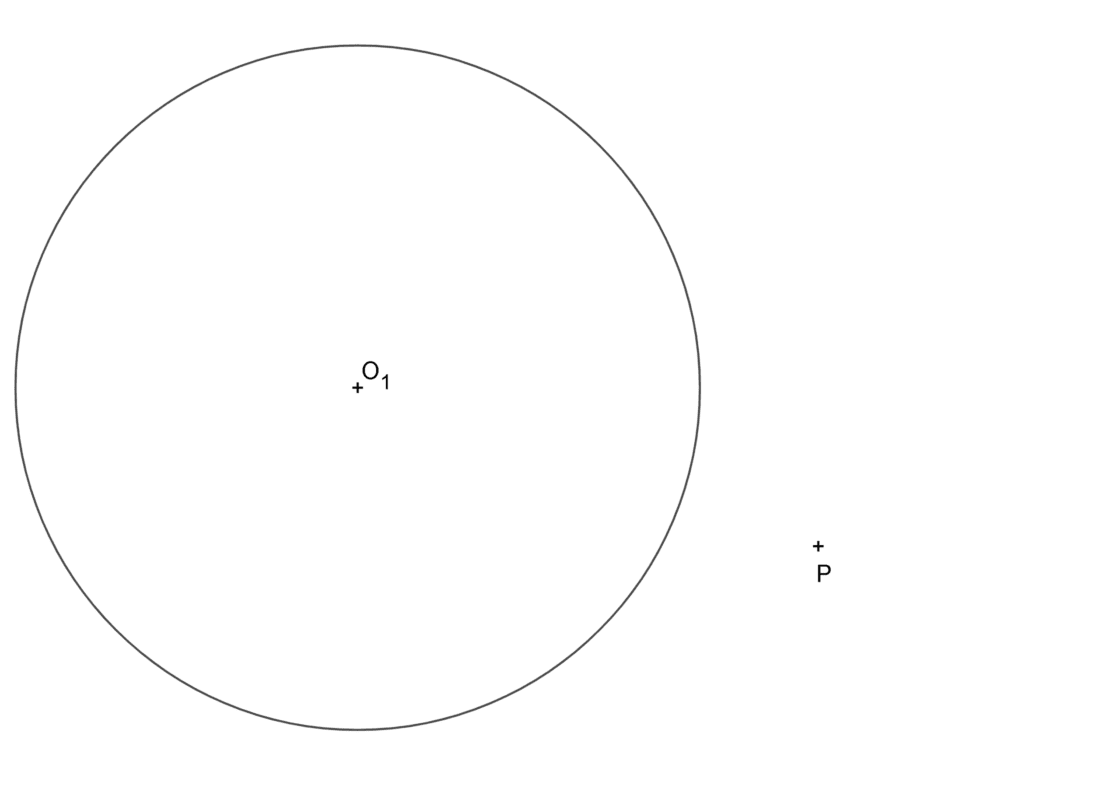
Empieza por dibujar una línea que una el centro de la circunferencia O₁ con P.
El siguiente paso es dibujar una recta perpendicular a esa línea que acabas de dibujar, y que pase por P.
Con un radio cualquiera, marca el centro O₂ sobre esa perpendicular, pero haz el radio bastante grande como para que luego la circunferencia de centro O₂ corte a la circunferencia de centro O₁
Ahora traza una circunferencia de centro O₂ y radio hasta P, esas dos circunferencias se cortan en los puntos B y A.
Dibuja la línea que pasa por B y por A. Esta línea corta a la que pasa por O₁ y P en el punto C.
Trazando una perpendicular a la recta que pasa por O1 y P que además pase por el punto C obtienes el eje radical que estás buscando.

¿Quieres ver algo curioso? La siguiente aplicación interactiva en apariencia es idéntica a la anterior, ¿verdad? Pues haz un pequeño experimento. Haz zoom sobre el punto P, verás lo que pasa.

Al igual que podemos decir que una recta es una circunferencia que tiene su centro en el infinito, podríamos afirmar que un punto es una circunferencia minúscula. Al ser tan pequeña, los puntos de corte de la circunferencia auxiliar se solaparán sobre la recta que une O₁ y P. En realidad P sería el centro de ésta circunferencia diminuta.

Eje radical de una circunferencia y una recta

Este problema tiene truco, ya que el eje radical es la propia línea. Así a simple vista igual resulta un poco difícil de entender. Intenta visualizarlo de otra forma… Imagina que la circunferencia es tan grande que el centro está en el infinito. En tal caso los puntos de corte de la circunferencia auxiliar que utilizas para cortar serán dos puntos de la recta. Eso siempre y cuando estés usando el método de la circunferencia secante.

Para que lo entiendas un poco mejor, te he preparado un ejemplo muy visual aquí a continuación. A simple vista no tiene nada de especial. Es el procedimiento habitual para hallar el eje radical de dos circunferencias. Pero he dejado todos los puntos fijos menos uno, el centro O₂. Haz lo siguiente:

Pon la aplicación a página completa usando el icono que parece un cuadrado que hay abajo a la derecha en la misma debajo de la lupa (lo verás mucho mejor).
Mueve el centro O₂ hacia la derecha.
Haz zoom usando la rueda del ratón para hacer mucho más pequeña la imagen.
Mueve el centro O₂ todavía más a la derecha y vuelve a hacer zoom para alejarte aún más.
Repite los pasos 2 y 3 un par de veces más.
Ahora haz zoom al revés, para acercarte y así ver bien la circunferencia de centro O₁.

Mira lo que pasa con los puntos C y D y lo que pasa con el eje radical. Seguro que te sorprende. Cuánto más te alejes, más se acercará la recta hacia la circunferencia. Si el centro estuviera en el infinito, la circunferencia sería una recta, y se solaparían.

Centro radical de tres circunferencias

El concepto de centro radical es muy semejante al del eje radical. La diferencia es que en éste caso se trata de un único punto. Hallar este punto es fácil, solo tienes que hallar los ejes radicales de dos pares de circunferencias. El punto donde se cortan es el único punto del plano en el que la potencia respecto a los tres ejes es la misma.

No voy a explicarte como se halla el centro radical porque como ya he dicho. Solo tienes que hallar los ejes radicales de dos pares de circunferencias y ver donde se cruzan. Si no sabes como, el proceso lo tienes justo antes de este. Para que practiques, aquí tienes una lámina que puedes imprimir.

Una pequeña aclaración… Ahora que ya conoces el concepto de centro radical, échale un ojo al inicio. A la forma de hallar el eje radical de dos circunferencias usando una circunferencia secante. Te lo voy a poner a continuación para que lo veas más rápido. Piensa un momento en el punto F y en las dos rectas que pasan por A, B y por C, D. ¿Qué son?

La recta que pasa por A y B es el eje radical de las circunferencias de centro O₁ y O₃.
El punto F es el centro radical de las tres circunferencias de centros O₁, O₂ y O₃.
Para terminar, la recta que pasa por C y D es el eje radical de las circunferencias de centro O₂ y O₃.

Circunferencias coaxiales

Las circunferencias coaxiales son aquellas que tienen la misma potencia respecto a una recta. Dicha recta es por tanto el eje radical de todas esas circunferencias. Existen tres casos distintos:

Que las circunferencias sean secantes.
Que las circunferencias sean tangentes.
Que las circunferencias sean externas.

En cualquier caso, date cuenta de que para que tengan el mismo eje radical, los centros de todas las circunferencias deben estar alineados. De no cumplirse esta propiedad, estaríamos hablando de un centro radical común a ellas. Los dos primeros casos son los más sencillos.

En el caso de circunferencias secantes, cualquier circunferencia que pase por los puntos de corte de ambas circunferencias y que tenga el centro alineado será coaxial de ambas. Si se trata de circunferencias secantes es similar. Cualquier circunferencia tangente a ambas en el punto de tangencia con el eje radical será coaxial también.

El más complicado es el tercer caso. Para resolverlo debes remitirte al segmento representativo de potencia que tienes al inicio de este post. Si te fijas, todas las circunferencias coaxiales tendrán la misma potencia si tomamos como referencia el punto donde la línea que une los centros de las circunferencias corta al eje (lo he llamado centro para no liar).

Si hallas el punto de tangencia del centro con una de las circunferencia, tienes el radio de la circunferencia que delimita los puntos de tangencia de todas las circunferencias. Aquí abajo puedes mover el punto P para verificarlo.