En esta ocasión vamos a ver como trazar distintos tipos de recta perpendicular con regla y compás. Pero en primer lugar…
¿Qué es una línea perpendicular?
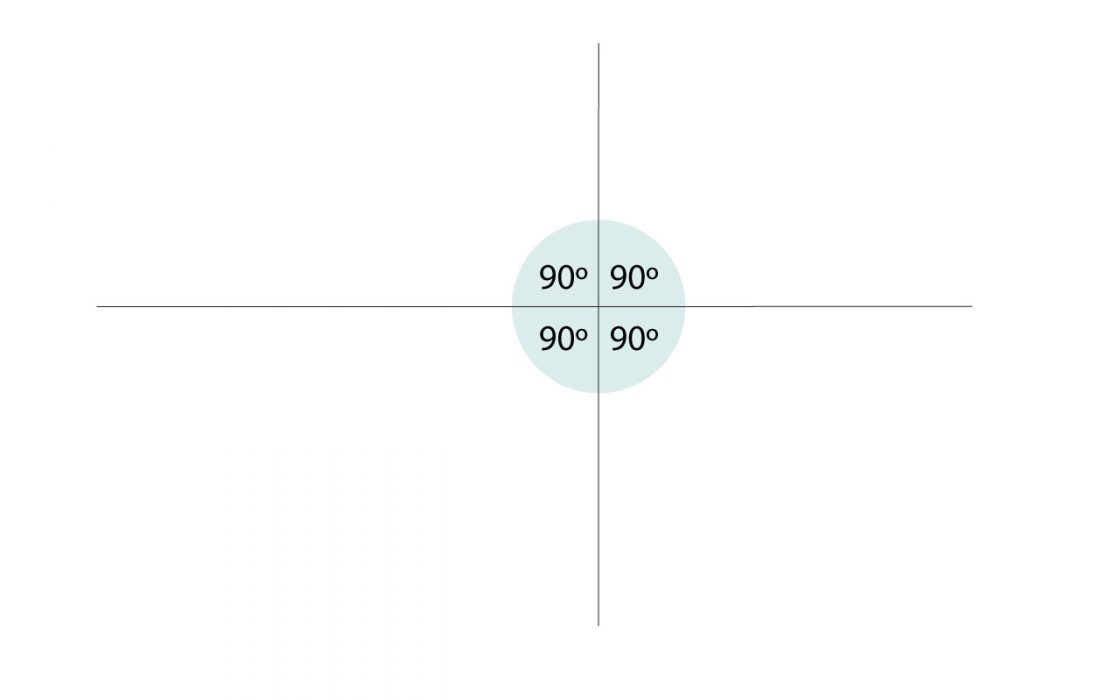
Si queréis una descripción científica, os recomiendo buscar en la RAE. Yo prefiero explicarlo de forma más sencilla. Una recta perpendicular a otra es la recta que forma un ángulo de noventa grados con la recta que corta. Si nos fijamos en dos rectas perpendiculares entre si, veremos que se crean cuatro ángulos de noventa grados. Es muy interesante la relación simétrica de las perpendiculares, que dice que si una recta r es perpendicular a una recta s, entonces la recta s será perpendicular a la recta r.
Dibujar una perpendicular a una recta por un punto de la misma
En éste caso te piden trazar una recta perpendicular a una recta dada r, por un punto P de la misma. Tu punto de partida es similar a esto y el procedimiento es el siguiente:
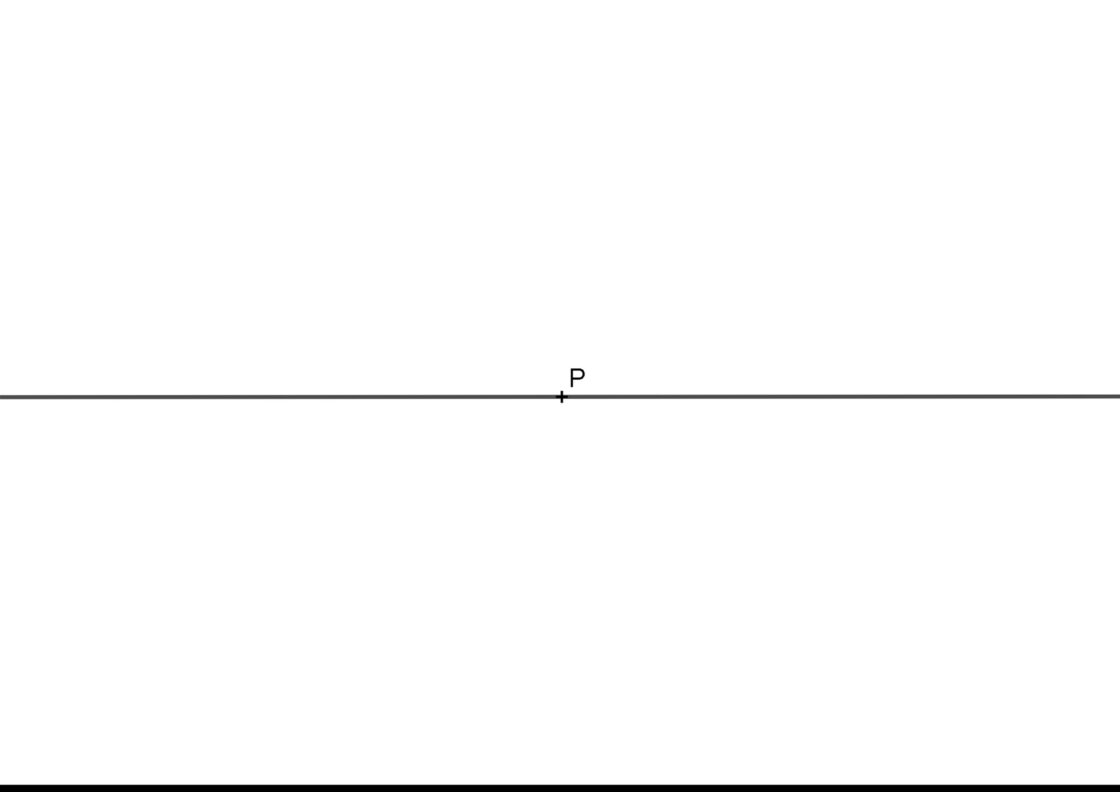
- Con el compás y una apertura cualquiera, pincha en el punto P.
- Con esa apertura, marca a la derecha un punto sobre la recta al que llamarás A.
- Ahora, sin levantar el compás, marca a la izquierda un punto al que puedes llamar B. Date cuenta de que tanto A, como B están a la misma distancia del punto P sobre la recta r.
- Pincha con el compás en A, y abre hasta B. Dibuja un arco que pase por encima y por debajo de P.
- Con esa misma apertura , con centro en B, dibuja otro arco que corta al anterior en el punto C y D.
- Dibuja la recta que pasa por C y D, esa es la recta s, perpendicular a la recta r.
Perpendicular a la recta por un punto externo a la misma
En este caso, se te pide dibujar una perpendicular a una recta por un punto P que no pertenece a la misma, por lo que tu punto de partida será parecido a esto. Para solucionarlo tienes que hacer lo siguiente:
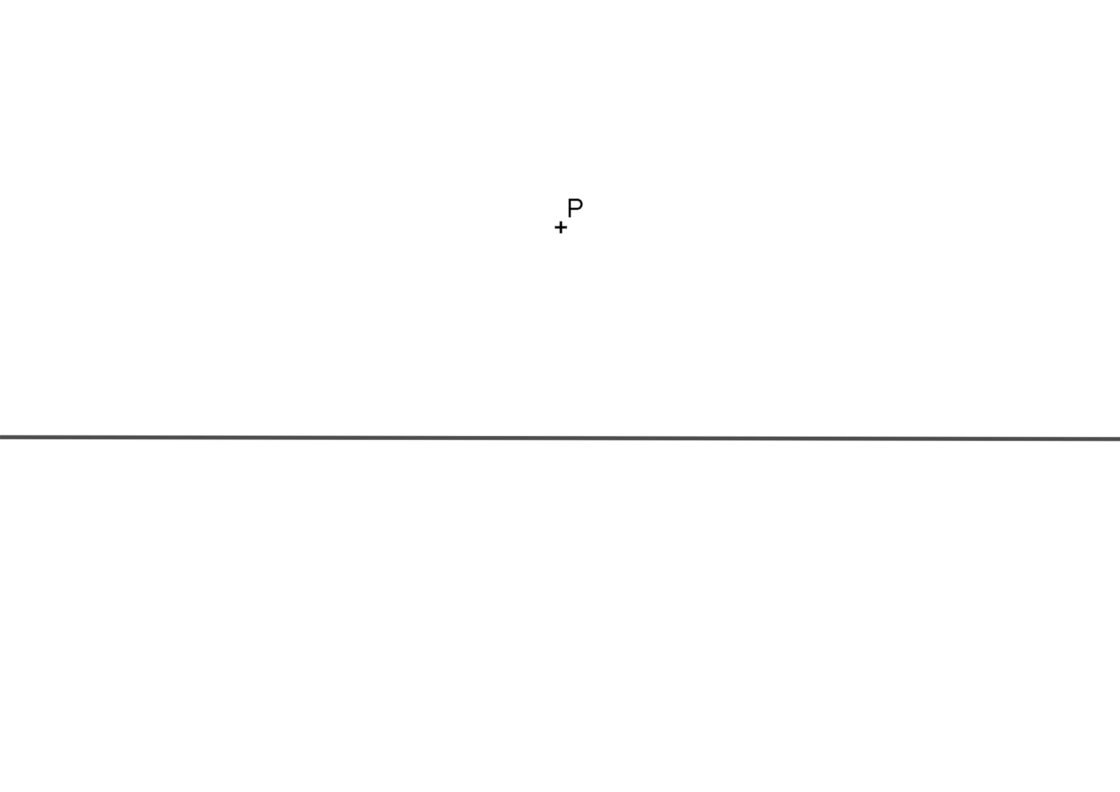
- Con centro en P y cualquier radio, dibuja un arco que corta a la recta en A y B, que están a la misma distancia de P.
- Ahora pincha con el compás en A y abre hasta B. Con esa medida dibuja un arco.
- No modifiques el tamaño en el compás y pincha en B. Traza un arco que cortará al anterior en los puntos C y D.
- Dibuja la recta que pasa por C y D. Esa recta es la perpendicular a la recta dada que pasa por el punto P.
Construcción de una mediatriz
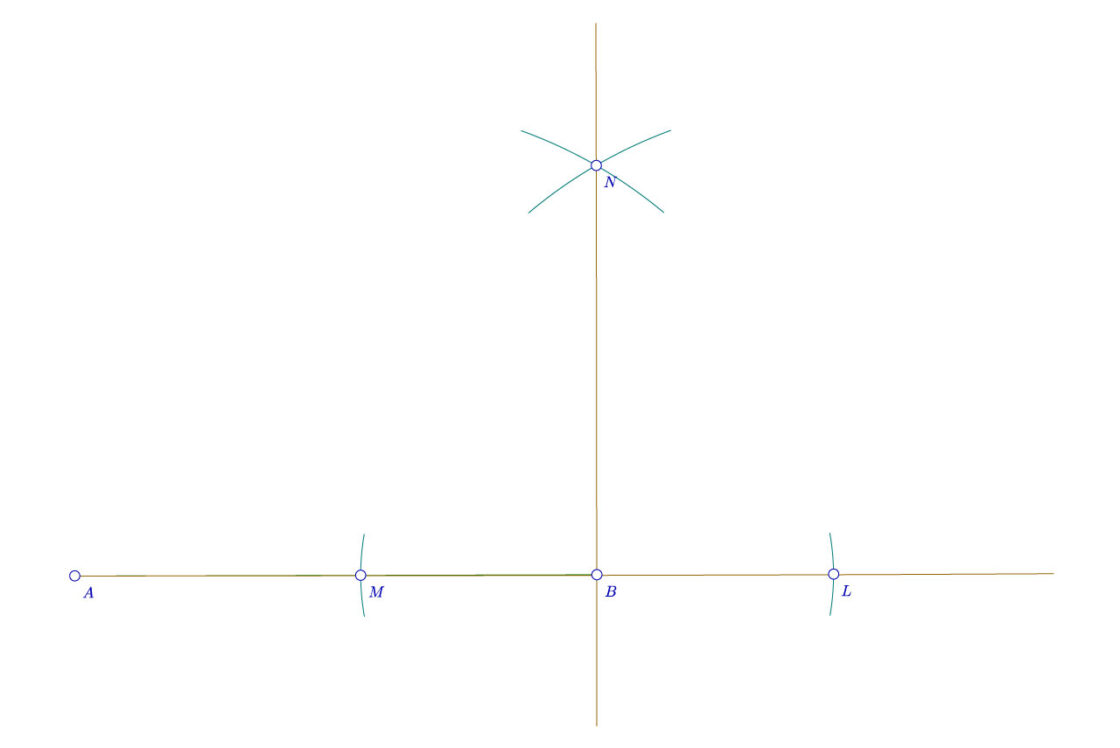
En primer lugar, aclarar lo que es una mediatriz por si no lo sabéis. Se trata de la recta perpendicular que se encuentra a la misma distancia de dos puntos de un segmento o recta. Así pues, si hablamos de la mediatriz de un segmento AB, es aquella recta cuyos puntos se encuentran a la misma distancia tanto de A como de B. Su uso es muy habitual cuando hablamos de simetría y divisiones. Vamos a ver cómo podemos trazar una perpendicular con compás gracias al concepto de mediatriz. Para este ejercicio tu punto de partida será este.
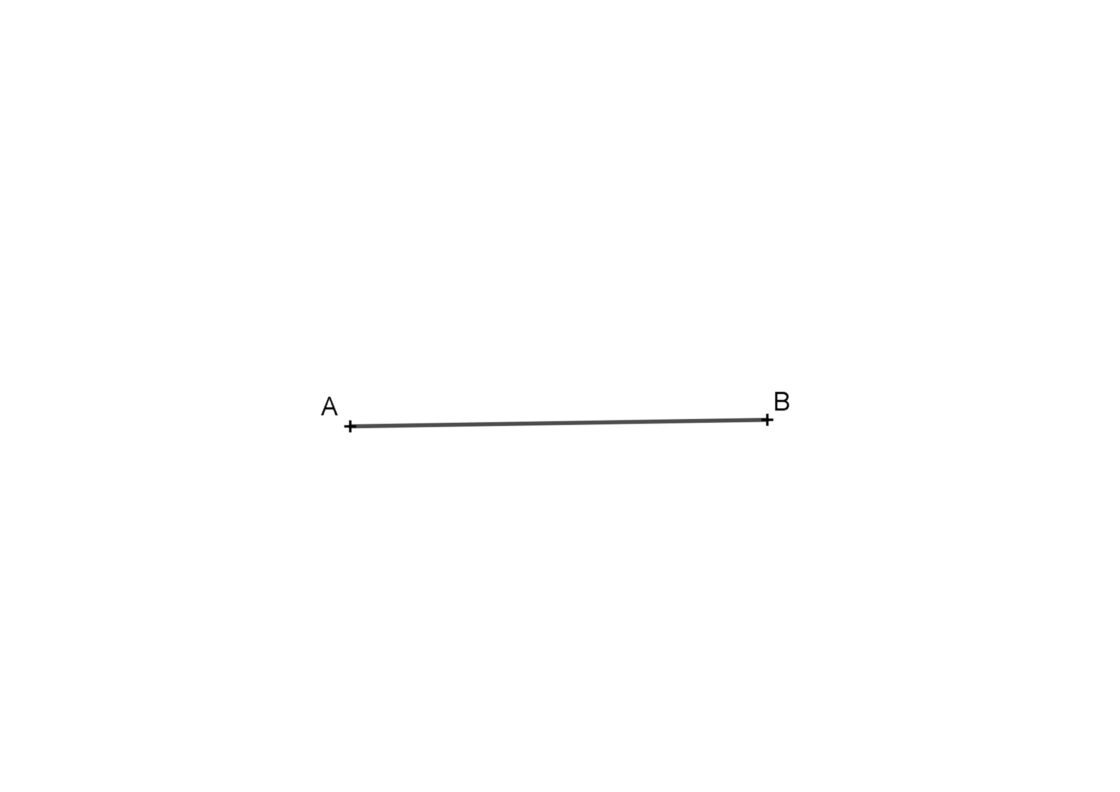
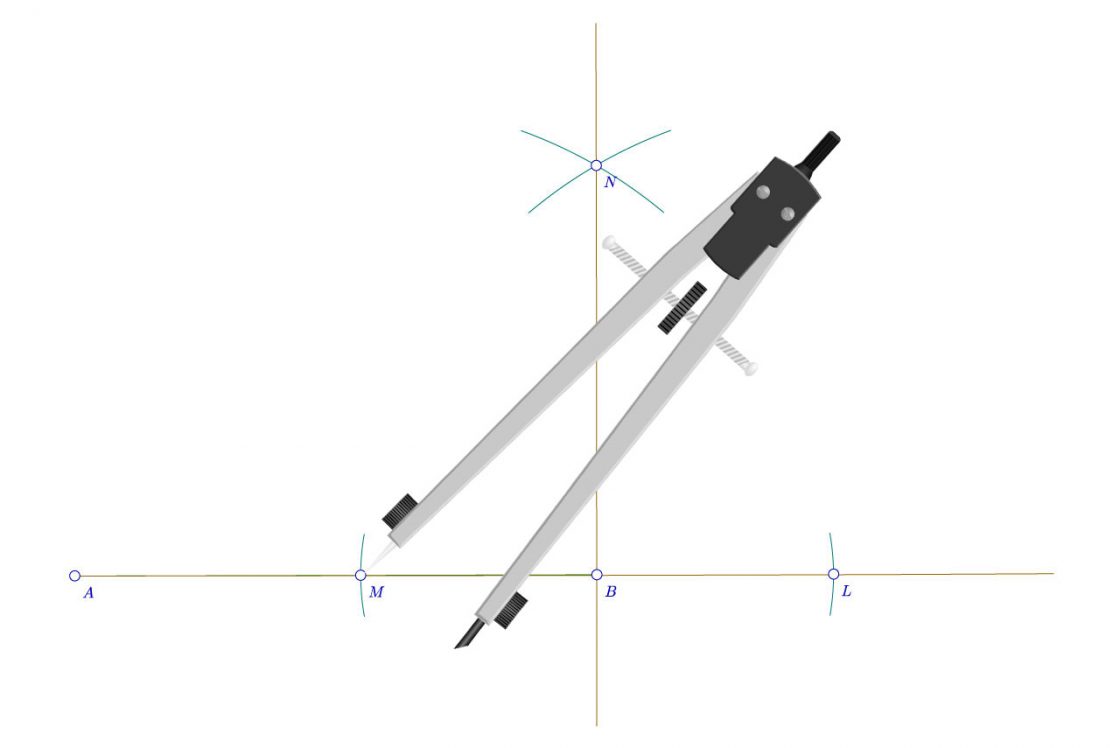
- En primer lugar, con centro en B y con una medida cualquiera, trazaremos dos arcos del mismo tamaño (arriba y abajo).
- Acto seguido trazaremos otros dos arcos desde A con la misma medida (esto es muy importante) que usamos para trazar los arcos desde B. De ese modo tendremos dos puntos de la recta mediatriz, que en éste caso he llamado E y D
- Para terminar, solo debemos dibujar la línea que une los puntos D y E para encontrar la mediatriz buscada.
Fijaos que al usar la misma medida para trazar los arcos desde A y B, sabemos seguro que el punto donde se cortan se encuentra a la misma distancia tanto de A como de B. Da igual la medida que tomemos siempre que sea la misma, y lo suficiente grande como para que se corten.
Trazar una perpendicular con compás por un extremo de un segmento o semirrecta
Construir una recta perpendicular con compás por el extremo de una semirrecta o segmento es muy similar al ejemplo anterior. Para ello solo tendremos que prolongar la recta sobre el extremo al cual queremos crear la perpendicular. Por ello nuestro punto de partida será parecido a esto.
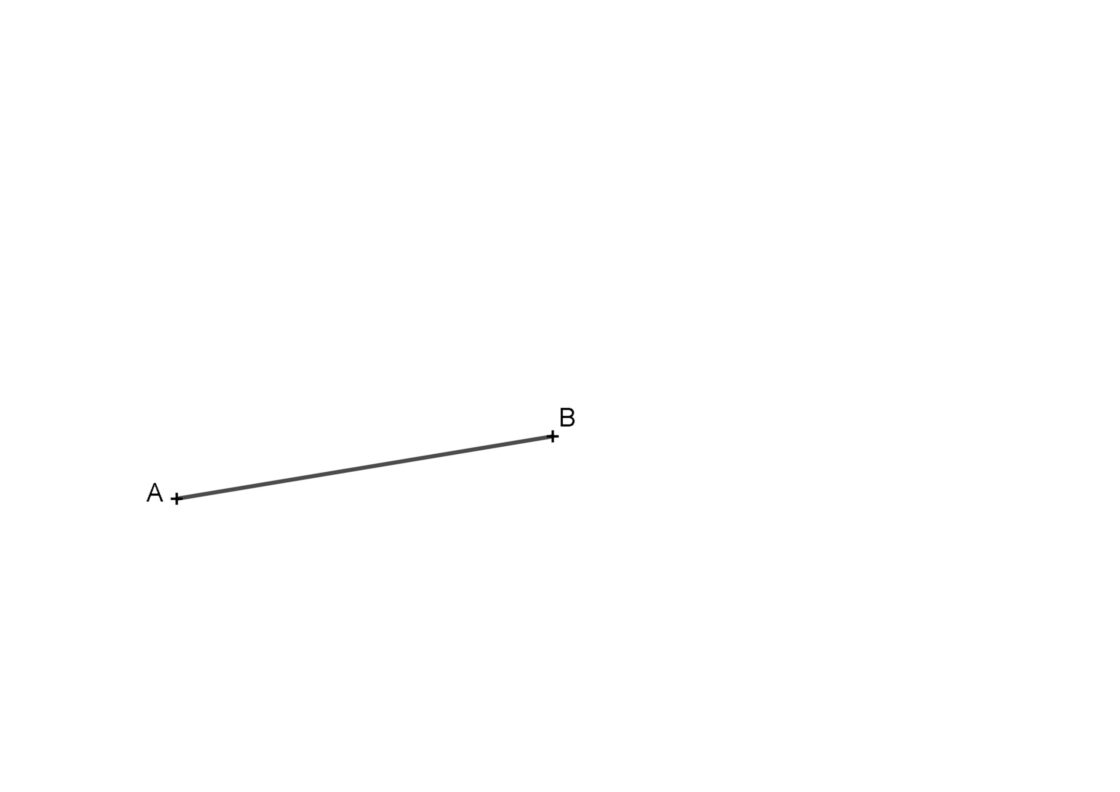
- En primer lugar, usando la regla, prolongaremos la semirrecta o segmento a partir del extremo en el cual queremos realizar la perpendicular. En éste caso vamos a trazarla pasando por el punto B, por lo que prolongaremos a partir de aquí.
- Ahora, con centro en B, realizamos un arco que corta al segmento y la recta prolongada en los puntos que he llamado C y D.
- Una vez tenemos los puntos C y D, con una distancia fija trazamos un arco desde C y otro arco desde D. Repito que es importante que la distancia sea la misma en ambos casos. Así obtenemos los puntos G y F, que se encuentran en la perpendicular deseada.
- Para terminar solo tenemos que unir G con F y ya tenemos el resultado deseado.
Aquí abajo tienes una aplicación interactiva en la que puedes mover los puntos para comprobar que la construcción siempre se cumple.
Trazar la perpendicular por el extremo de un segmento, sin prolongarlo
Hay situaciones en las que por el motivo que sea no podremos prolongar un segmento. Bien porque se encuentra cerca del límite del papel, o por cualquier otro motivo. En éste caso será imposible utilizar el método tradicional usando puntos auxiliares. Pero os voy a explicar un método alternativo que también funciona. En este caso el punto de partida es similar al anterior, algo parecido a esto.

- En primer lugar, con centro en el extremo por el cual queremos realizar la perpendicular trazaremos un arco con una longitud cualquiera, cortando al segmento en el punto H. El arco lo hacemos un poco grande, porque luego lo vamos a necesitar.
- Con esa misma distancia, pero desde el punto H trazamos otro arco que corta al anterior en el punto I
- Trazamos una semirrecta desde el punto H al punto I, prolongándola un poco.
- Con centro en I, y radio igual a la distancia entre I y B, trazamos un arco que corta a la semirrecta que hemos dibujado antes en el punto J
- Uniendo el punto J con el punto B tenemos la perpendicular buscada.
Aquí abajo tienes una aplicación interactiva para ver cómo queda.
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti. Gracias de antemano por dejar tu comentario un poco más abajo.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
