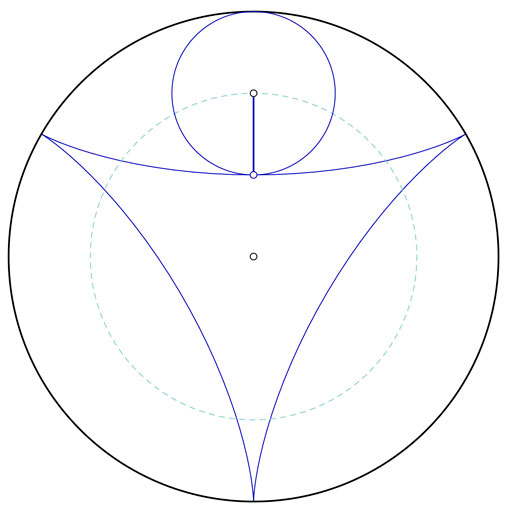
La hipocicloide en dibujo técnico pertenece al grupo de las curvas cíclicas, dentro del grupo de las curvas técnicas que se produce cuando una circunferencia gira en el interior de otra. Se trata de la marca que dejaría un punto sobre la circunferencia interior, de menor radio. Puede encontrarse sobre la propia circunferencia, o bien en el interior del círculo o en el exterior del mismo, dando lugar a hipocicloides alargadas o acortadas.
En la aplicación interior puedes modificar el radio grande y el radio pequeño para ver algunas de las posibilidades. También puedes desplazar la barra de movimiento, para ver como se comporta en el tiempo
Como dibujar una hipocicloide normal en dibujo técnico
El procedimiento es prácticamente el mismo que el empleado en la epicicloide, con la excepción de que la ruleta gira por el interior. Si ya sabes dibujar epicicloides, este procedimiento lo vas a encontrar realmente sencillo. Antes de empezar, en un papel aparte, deberías rectificar un arco de 90 grados de la ruleta. Luego realizar el proceso inverso para ver cuanto avanza sobre la circunferencia estática. Aquí abajo tienes el proceso completo, pero puedes revisar la entrada sobre las rectificaciones de arcos si quieres más detalles. Así sabes cuanto avanza la ruleta sobre la circunferencia grande con un cuarto de vuelta. Luego solo tienes que llevarlo cuatro veces para hallar el desplazamiento de una vuelta completa.
Para hacer las cosas más sencillas, si quieres practicar este ejercicio, utiliza las siguientes medidas: Circunferencia grande, 15cm radio. Ruleta, 5cm radio. De esa manera sabes que una vuelta entera de la ruleta corresponde a un tercio de la circunferencia grande y te evitas tener que hacer las rectificaciones. Tu punto de partida debería ser algo semejante a esto:
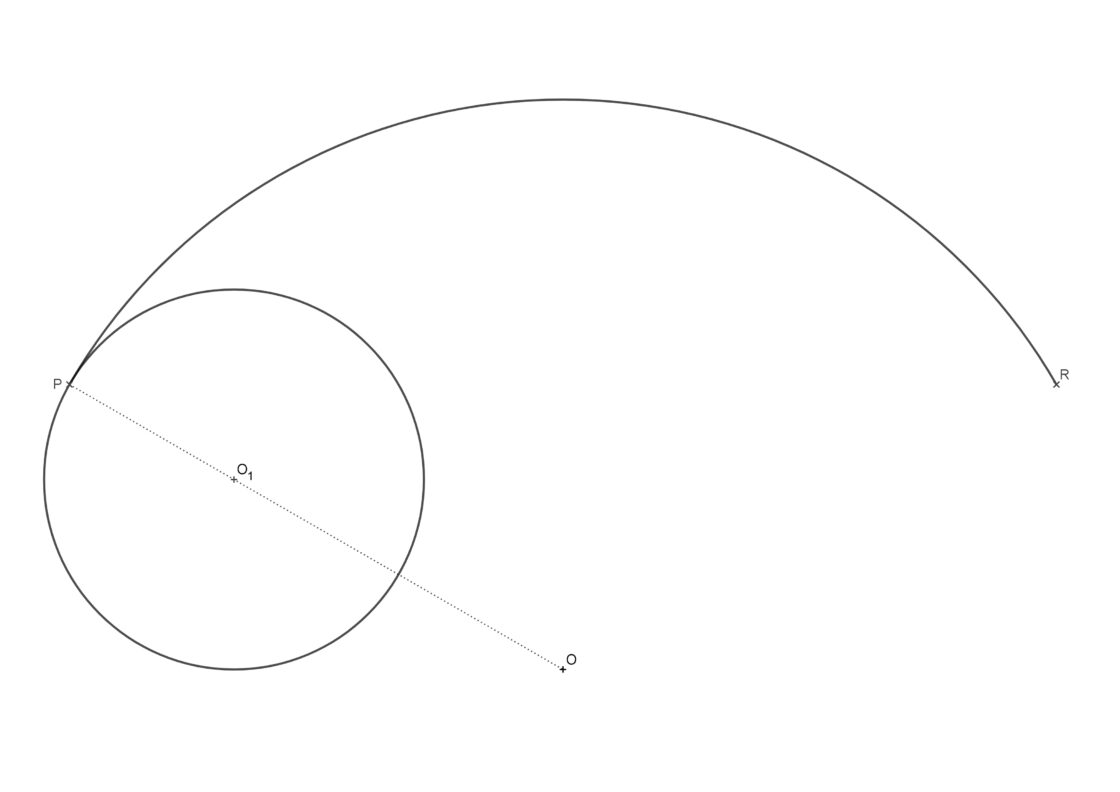
Si quieres puedes pulsar sobre la imagen para abrirla a pantalla completa e imprimirla en un DIN A4 para mayor comodidad.
- Empieza por dividir el arco de la circunferencia grande en ocho partes. Cada una de ellas corresponderá con la posición del centro de la ruleta en cada una de esas partes. La forma más fácil es haciendo bisectrices.
- Haz un arco con centro en O y radio hasta O1. Donde este arco corta a las bisectrices que dibujaste antes tienes O2, O3, O4, etc. Estos puntos corresponde con la posición del centro de la ruleta cada vez que gira una octava parte de vuelta.
- Ahora divide media ruleta en cuatro partes para hallar los puntos R, S y T.
- Con el compás, y centro en O (centro de la circunferencia mayor) traza arcos con radio hasta Q, R, S y T. Deberías tener algo parecido a lo siguiente.
5. Si tenemos en cuenta que el punto P es el que dibuja la hipocicloide, vamos a dibujar la curva tomándolo como referencia.
6. El siguiente punto lo tienes trazando un arco con centro en O2 y radio igual al de la ruleta. Donde corta a la curva de R tienes el punto P2.
7. Con centro en O3 y radio igual al de la ruleta, traza un arco que corta a la curva de S. Donde cortan tienes el punto P3.
8. El punto P4 lo tienes donde el arco de T corta a la circunferencia de centro igual a la ruleta y de centro O4.
9. Si te fijas, el punto P5 está justo en la mitad, y marca un eje de simetría. Los demás puntos son simétricos de los que has dibujado antes.
10. Para hallar P6 es donde corta a la curva de T.
11. Encontrarás P7 en el corte con la curva de S.
12. A el punto P8 lo tienes en la intersección con la curva de R.
13. Para terminar, P9 lo tienes de nuevo arriba, sobre la curva.
14. Une esos puntos de tres en tres con la plantilla de curvas y ya tienes tu hipocicloide.
Aquí abajo tienes una hipocicloide interactiva, por si te cuesta entender el desarrollo. Puedes mover el punto R para ver como se deplaza P y la curva que dibuja.
