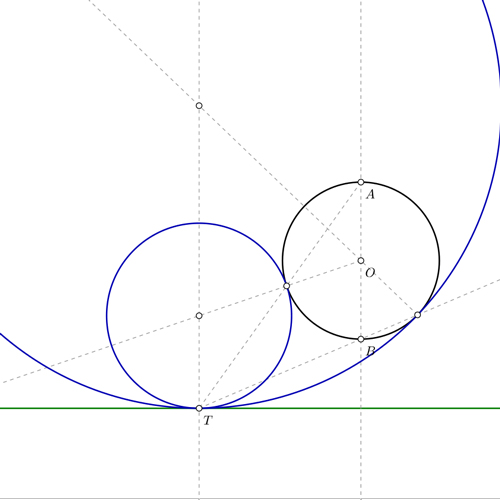
La utilización de la inversión para la resolución de circunferencias tangentes es un recurso muy utilizado para determinados tipos de ejercicios. Los problemas que te propongo en ésta sección son referidos al nivel de segundo de bachillerato. Son una alternativa a la utilización del concepto de potencia para la resolución de tangencias.
Para resolver estos ejercicios es imprescindible dominar las tangencias básicas de primero de bachillerato. Si todavía no las controlas, te recomiendo repasar antes la entrada donde hablo de las propiedades básicas de las tangencias y los ejercicios más elementales.
Circunferencias tangentes a una circunferencia y un punto de una recta recta
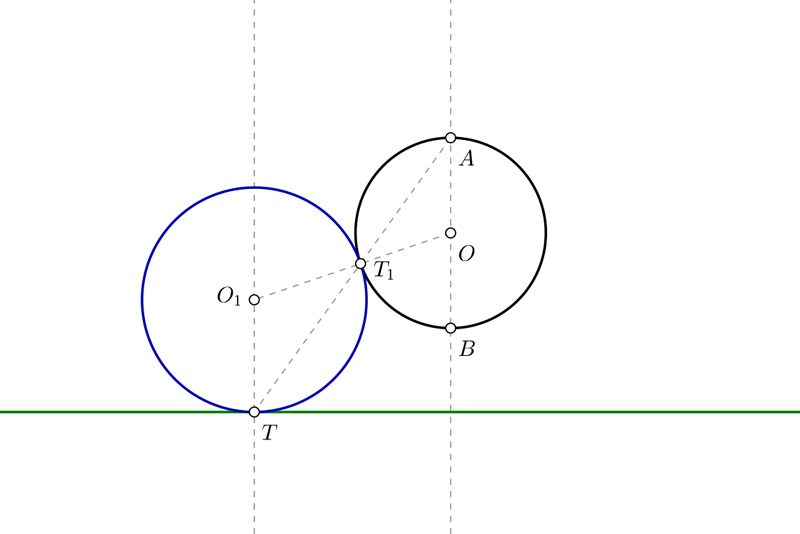
También puedes usar la inversión en circunferencias tangentes para resolver este tipo de ejercicios. En ésta ocasión conoces el punto de tangencia T sobre una recta r que te proporcionan. También conoces una circunferencia concreta, y te piden hallar las circunferencias tangentes a esa circunferencia que pasan por el punto T.
- Dibuja una recta perpendicular la recta conocida por el punto T. Si recuerdas las propiedades de las tangencias, los centros de las circunferencias que buscas estarán sobre esa perpendicular.
- Ahora dibuja una recta perpendicular a la recta r que pase por el centro de la circunferencia que conoces. Esta recta corta en los puntos A y B. Esos puntos son los centros de inversión negativa y positiva.
Primera circunferencia
- Traza una recta desde A hasta T. Esa recta corta a la circunferencia en el punto T1, que es uno de los puntos de tangencia.
- Une el centro de la circunferencia con el punto T1 y prolonga esa recta para ver donde corta a la perpendicular que pasa por T.
- El punto de corte es O1, centro de la primera circunferencia.
- Con centro en O1 y radio hasta T ó T1 puedes trazar la primera circunferencia.
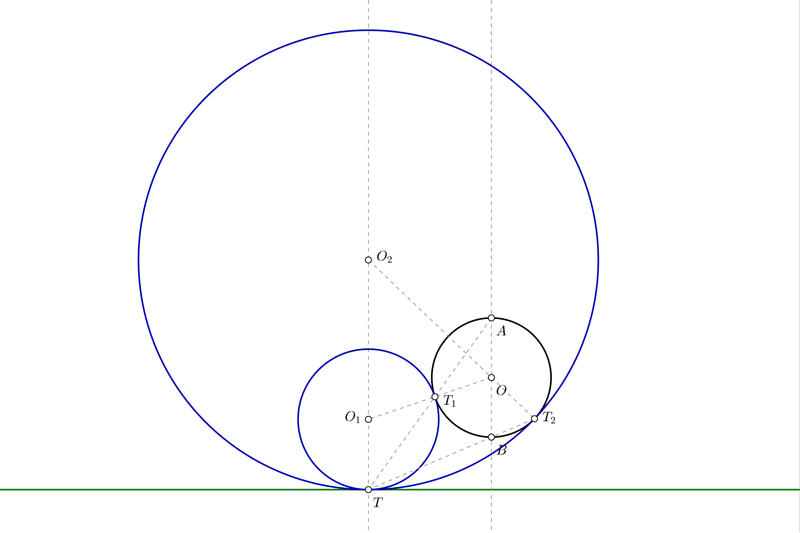
Segunda circunferencia
- Une T con B, en su prolongación corta a la circunferencia en el punto T2, que es el otro punto de tangencia que buscas.
- Une T2 con el centro de la circunferencia para ver donde corta a la perpendicular que pasa por T. Ese punto es el centro O2 de la otra circunferencia que estás buscando.
- Con centro en O2 y radio hasta T ó T2, puedes dibujar la otra circunferencia que estás buscando.
En la siguiente aplicación interactiva puedes mover los puntos azules para verificar como se comportan este tipo de tangencias y comprender un poco mejor su construcción.
Circunferencias tangentes a una recta y un punto de una circunferencia
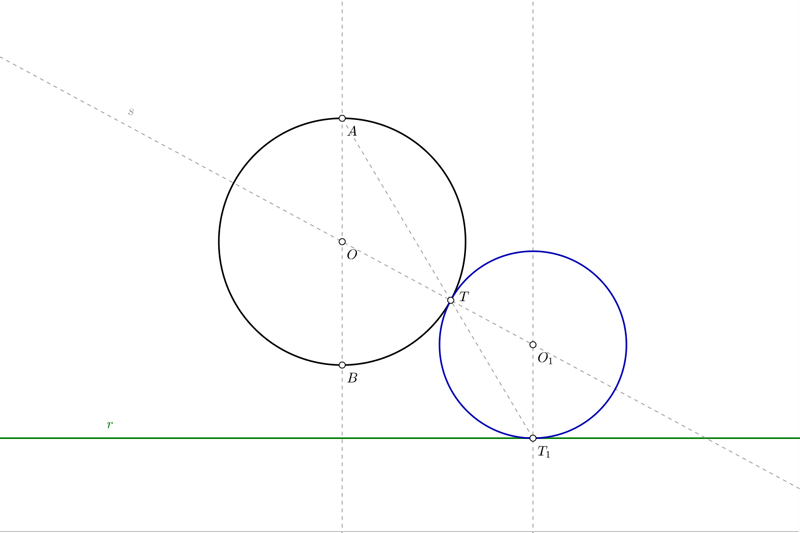
Para resolver éste tipo de ejercicios te proporcionan una recta r y una circunferencia concreta de centro O. También conoces el punto de tangencia T sobre la circunferencia.
- Empieza dibujando la recta que une el centro de la circunferencia O con T. Sobre esa recta estarán los centros de las dos circunferencias que buscas. Una de ellas contendrá a la circunferencia y la otra estará fuera de ella. A ésta recta la llamaremos s.
- Acto seguido dibuja una recta perpendicular a la recta r que pase por el centro de la circunferencia. Como en el caso anterior, los puntos donde corta a la circunferencia los llamamos A y B, que son los centros de inversión negativa y positiva.
Resolución de la primera circunferencia
- Para hallar la primera circunferencia, une A con T y prolonga para ver donde corta a la recta r. A éste punto lo llamaremos T1, porque es el primer punto de tangencia.
- Levanta una perpendicular a la recta r que pase por T1. Donde corta a la recta tienes el punto O1, centro de la primera circunferencia tangente.
- Con centro en O1 y radio hasta T1 ó T, dibuja la primera circunferencia tangente que buscas.
Resolución de la segunda circunferencia
- Une el punto de tangencia T con el punto B, y prolonga hasta cortar a la recta r en el punto T2
- Levanta una perpendicular a la recta r que pase por T2, ésta perpendicular corta a la recta s (la que une O con T) en un punto al que puedes llamar O2, porque es el centro de la otra circunferencia.
- Con centro en O2 y radio hasta T2 ó T, puedes dibujar la segunda circunferencia, y de ese modo resolver el problema.
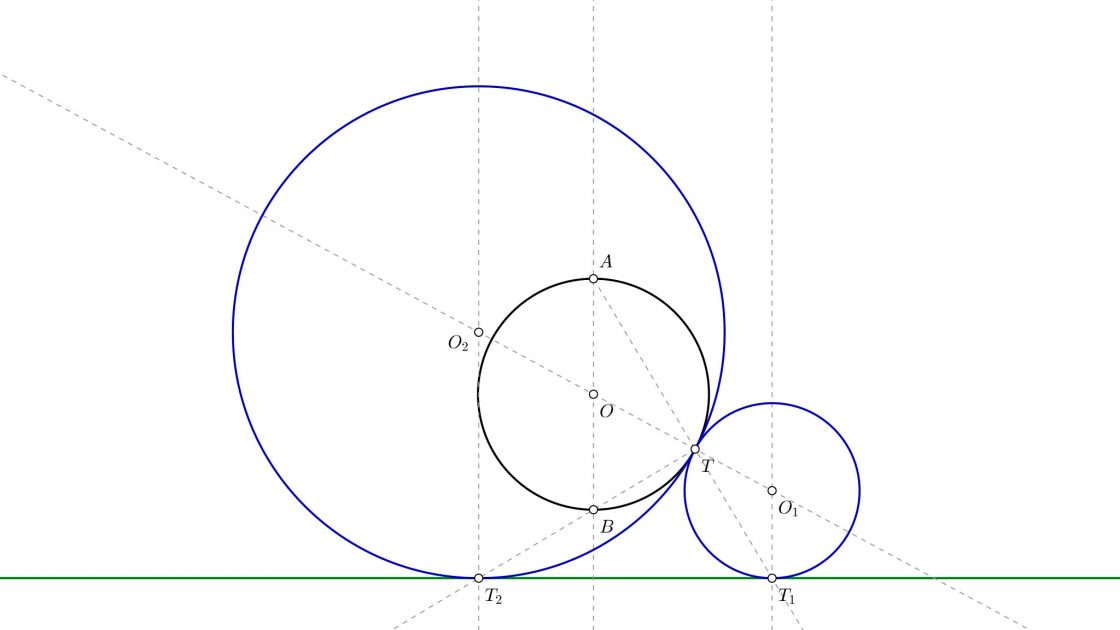
Aquí abajo tienes una aplicación interactiva que te ayudará a comprender un poco mejor esta construcción. Puedes mover los puntos azules para comprobar que se cumple en cualquier caso.
Circunferencias tangentes a dos circunferencias y que pasan por un punto exterior P
Este ejercicio es bastante complejo. En su resolución vas a encontrar cuatro soluciones posibles. Una circunferencia pequeña que no contendrá ninguna circunferencia. Dos distintas que contendrán a la circunferencia de centro O1 por un lado y la otra a la de centro O2. Por último una que contendrá a ambas. Para que puedas practicarlo cómodamente te pongo a continuación una lámina que puedes imprimir en formato DIN A4 en cualquier impresora doméstica. Así pues, tu punto de partida se parecerá a esto:
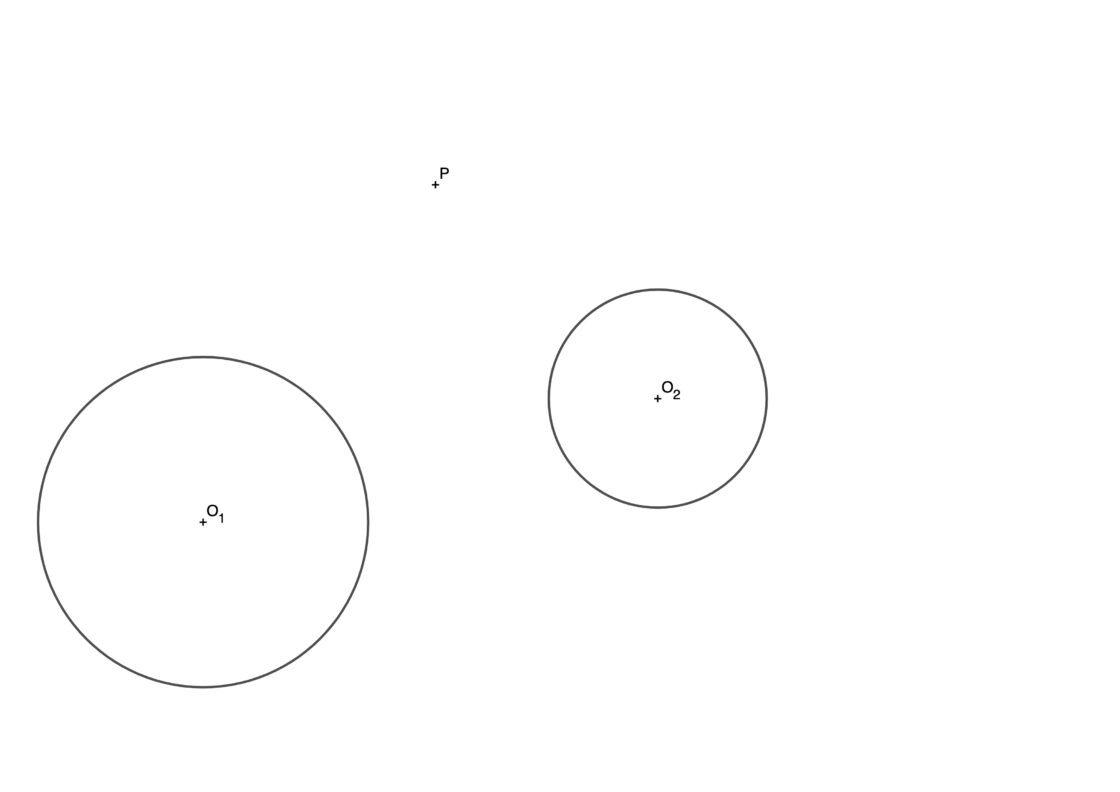
Con esta lámina puedes dibujar la circunferencia tangente de menor tamaño, las otras tres no se suelen pedir. Para resolverlo vamos a considerar que P es el centro de inversión. A continuación te explico como resolverlo paso a paso, y ya de paso algunos conceptos sobre la inversión.
Primera circunferencia: Sin contener ninguna circunferencia
- Empieza por hallar los puntos de tangencia de las rectas que pasan por P y que son tangentes a la circunferencia de centro O1. Al punto de tangencia llámalo B.
- Con centro en P y radio hasta B dibuja una circunferencia. Como P es el centro de inversión, ésta circunferencia es la circunferencia de autoinversión de la potencia igual a la raíz cuadrada de PB.
- La circunferencia de autoinversión corta a la otra circunferencia en el punto C, que utilizarás después.
- Dibuja una línea que pase por P y O2. El objetivo es hallar la circunferencia inversa a la de centro O2. Como todos los puntos están alineados respecto al centro de inversión P, el centro O3 de la circunferencia inversa de O2 estará sobre esa línea.
- La línea que has dibujado antes corta a la circunferencia de centro O2 en el punto D. Dibuja una recta perpendicular a esa recta que pase por D. Esa perpendicular corta a la circunferencia de centro P y radio PB en el punto E.
- Dibuja una perpendicular al radio PE que pase por E. Esa perpendicular corta a la recta que pasa por P y O2 en el punto F. Como aclaración, el punto F es el punto inverso de D. Por lo tanto, tanto C como F pertenecen a la circunferencia inversa a la de centro O2.
- Si trazas la mediatriz del segmento CF, donde este segmento corta a la recta que pasa por P y O2, tienes el centro O3, que es el centro de la circunferencia inversa de la de centro O2.
- Halla las rectas tangentes a las circunferencias de centro O1 y O3, de momento solo vas a usar la más alejada de P. Esta recta te permitirá hallar la circunferencia más pequeña, que no contiene a ninguna de las dos iniciales. Si no recuerdas como hallar las rectas tangentes a dos circunferencias, te recomiendo visitar la entrada donde explico los problemas básicos de tangencias.
- Los puntos de tangencia de esa recta con las circunferencias llámalos T1 y T2. Une P con T1 por un lado con una recta y con T2 con otra recta. Donde esas rectas cortan a las circunferencias iniciales tienes los puntos T3 y T4.
- Los puntos T3 y T4 son los puntos de tangencia de la circunferencia que estás buscando. Para hallar el centro solo tienes que dibujar rectas que pasen por O2 y T4 por un lado y por O1 y T3 por el otro. El lugar donde se cortan en O4, centro de la circunferencia que buscas.
- Con centro en O4 y radio hasta P, dibuja la circunferencia solución. Esta circunferencia es tangente a ambas circunferencias y además pasa por P.
Segunda circunferencia: Conteniendo a ambas circunferencias
Para hallar la segunda, halla las rectas tangentes a las circunferencias de centro O1 y O3. Si en el ejemplo anterior usaste la recta tangente más alejada, en este caso usarás la más cercana. Los puntos de tangencia serán T1 y T2
Traza líneas que unan P con T1 y T2, donde la prolongación de la recta que une P con T1 corta a la circunferencia de centro O1 tienes el punto T3 y donde la recta que une P con T2 corta a la circunferencia de centro O2 tienes T4
Para hallar el centro de la circunferencia resultante solo tienes que trazar rectas que pasen por T3 y O1 por un lado y por T4 y O2 por el otro. Donde cortan tienes O4, el centro de la circunferencia que buscas.
El paso final es pinchar con el compás en O4, abrir hasta P, T3 o T4 y trazar la circunferencia
Tercera circunferencia: Conteniendo a la menor
Para hallar esta circunferencia tienes que hallar las rectas tangentes interiores a las circunferencias de centros O1 y O3 para este ejercicio solo tomaremos una de ellas. Al punto de tangencia con la circunferencia de centro O1 lo llamaremos T1 y al punto de tangencia con la circunferencia de centro O3 lo llamaremos T2
Como en casos anteriores, traza las rectas que unen P con T1 y T2. La recta que une T1 con P corta a la circunferencia de centro O1 en T3, y la prolongación de la recta que une P con T2 corta a la circunferencia de centro O2 en T4
Sabiendo los puntos de tangencia, puedes hallar el centro de la circunferencia igual que hicimos en el ejercicio anterior.
Cuarta circunferencia: Conteniendo a la mayor
Este caso se resuelve como el anterior, pero tomando como referencia la recta interior tangente que no tomamos antes. Ten cuidado al hallar T4, ya que la recta que une P con T2 corta a la circunferencia de centro O2 en dos puntos, pero solo uno de ellos es el punto de tangencia.
Circunferencias tangentes a una circunferencia y una recta, que pasan por P
Este ejercicio es similar al anterior. La única diferencia es que en el enunciado se cambia una circunferencia por una recta. De todas formas, si recuerdas lo aprendido en lecciones anteriores, una recta es una circunferencia con el centro en el infinito.
Circunferencias tangentes a una recta y una circunferencia por un punto exterior P
Este ejercicio es igual que el anterior. La diferencia radica en que cambia una circunferencia por una recta. Pero esto no es problema si recuerdas que la figura inversa de una circunferencia que pasa por el centro de inversión es una recta. Si no lo acabas de ver claro, te recomiendo visitar el artículo donde hablo de la inversión en geometría. Otra forma de interpretarlo es recordar que una recta se puede concebir como una circunferencia cuyo centro se encuentra en el infinito. Como en el anterior, también hay cuatro posibles soluciones.
Como practicar este ejercicio poniendo los puntos de manera arbitraria es un poco complicado, aquí tienes una lámina que puedes imprimir en DIN A4 para poder realizar este ejercicio. En un principio esta lámina está pensada para poder realizar sin problemas la circunferencia tangente más pequeña. Las otras tres no se suelen pedir. Así pues, tu punto de partida se parece a esto:
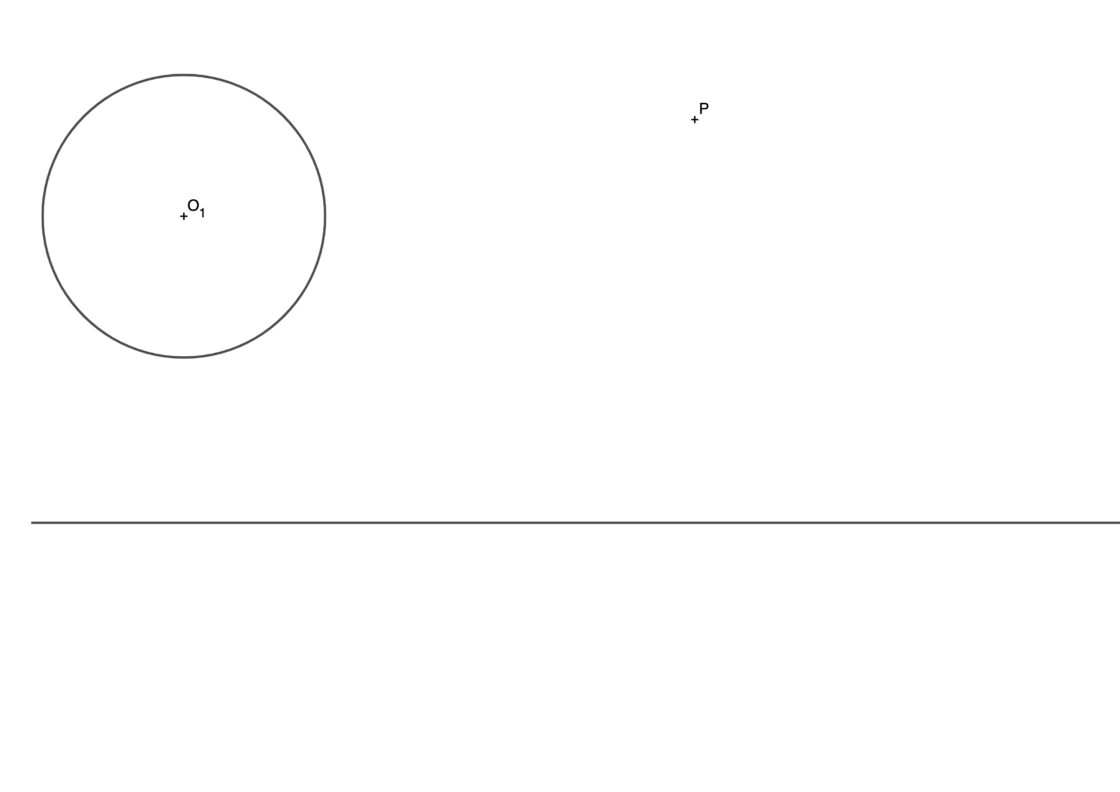
Primera circunferencia tangente: La menor, que no contiene a la circunferencia
- El primer paso será hallar la figura inversa de la recta. Para ello empieza por hallar las rectas tangentes a la circunferencia de centro O1 que pasan por P. Realmente solo necesitas un punto de tangencia, que llamaremos B.
- Con centro en P y radio PB, dibuja un arco de circunferencia que corta a la recta en los puntos C y D. Como información adicional, date cuenta de que ese arco forma parte de la circunferencia de puntos dobles. Es decir, C y D son dobles de sí mismos y coincidirían con C’ y D’.
- Dibuja una perpendicular a la recta que pase por P.
- A continuación traza la mediatríz del segmento PD, hallando el punto O3, que es el centro de la circunferencia inversa a la recta dada.
- Traza una circunferencia de centro O2 y radio O2P.
- Halla los puntos de tangencia de las rectas tangentes a las circunferencias de centro O1 y O2. Estos puntos llámalos T1 y T2.
- Une P con T1 con una línea por un lado, y P con T2 por el otro con otra línea. Los puntos donde estas líneas cortan a la recta y la circunferencia de centro O1 llámalos T3 y T4 respectivamente.
- Ahora dibuja una línea que pase por O1 y T3 por un lado, y por otro lado una perpendicular a la recta que pase por T4. Donde esas dos líneas se cruzan tienes el centro O3.
- Para terminar, con centro en O3 y radio O3P, dibuja la circunferencia solución que estás buscando.
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti. Gracias de antemano por dejar tu comentario un poco más abajo.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
