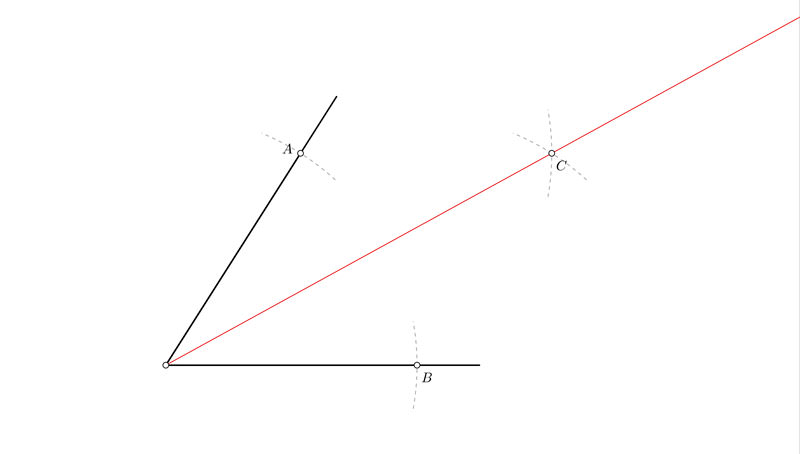
Recordemos que la bisectriz de un ángulo es la recta que divide dicho ángulo en dos partes iguales. Esta operación es uno de los trazados básicos que debemos aprender, pues de ello dependerá también como realizar operaciones más complejas que encontraremos más adelante.
Como hallar la bisectriz de un ángulo
No importa si el ángulo es obtuso, recto o agudo, el proceso es exactamente el mismo. Como podéis ver es muy sencillo:
- Con centro en el vértice y cualquier radio, trazamos un arco que corta a los lados del ángulo en los puntos A y B.
- Con esa misma medida, y desde los puntos A y B, trazamos dos arcos que cortarán en un punto al que llamaremos C.
- Si unimos C y el vértice del ángulo, tendremos la recta que delimita la bisectriz que estamos buscando.

Para practicar, prueba a hallar la bisectriz de un ángulo de 60º, de esa manera podrás verificar de forma muy fácil el resultado usando el cartabón. Tu punto de partida será este.
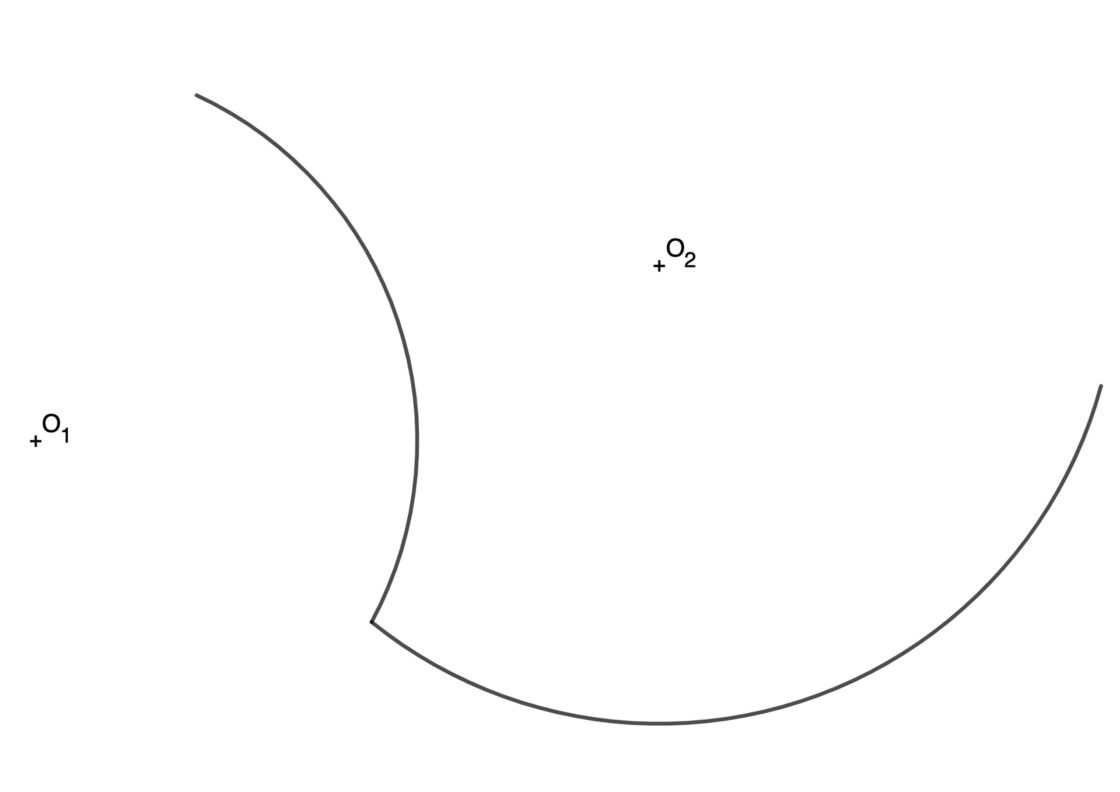
Bisectriz del ángulo curvilíneo
En primer lugar, recordar que cuando hablamos de ángulos compuestos por una o dos curvas, la cosa cambia. La bisectriz ya no se hace teniendo en cuenta el ángulo en si, sino la distancia de los puntos de la bisectriz a los lados del ángulo, que siempre es la misma. Tu punto de partida se parecerá a ésto.
- En primer lugar unimos una linea auxiliar que una el punto O1 y O2
- Con centro en el punto de corte con el arco de O1 que vamos a llamar A, trazamos un arco cualquiera que corta a la línea auxiliar en C
- Siempre con la misma medida, repetimos la operación, obteniendo los puntos C, D y E
- Exactamente con la misma distancia, pero desde la circunferencia de centro O2 marcaremos varios puntos adicionales. Yo he partido del punto de corte de la recta auxiliar con la circunferencia para facilitar el proceso y tener menos lío de líneas. Los puntos que hemos obtenido son I, H y G
- Trazamos una circunferencia auxiliar con centro en O1 y radio hasta C y después una circunferencia auxiliar con centro en O2 y radio hasta G. El punto J donde se cortan se encuentra a la misma distancia de ambas curvas.
- Repetimos la operación con C y H, obteniendo el punto K. Después lo repetimos con el punto I y el punto E, obteniendo el punto L
- Si unimos el vértice del ángulo curvilíneo con J, K y L, obtendremos la curva que forma la bisectriz
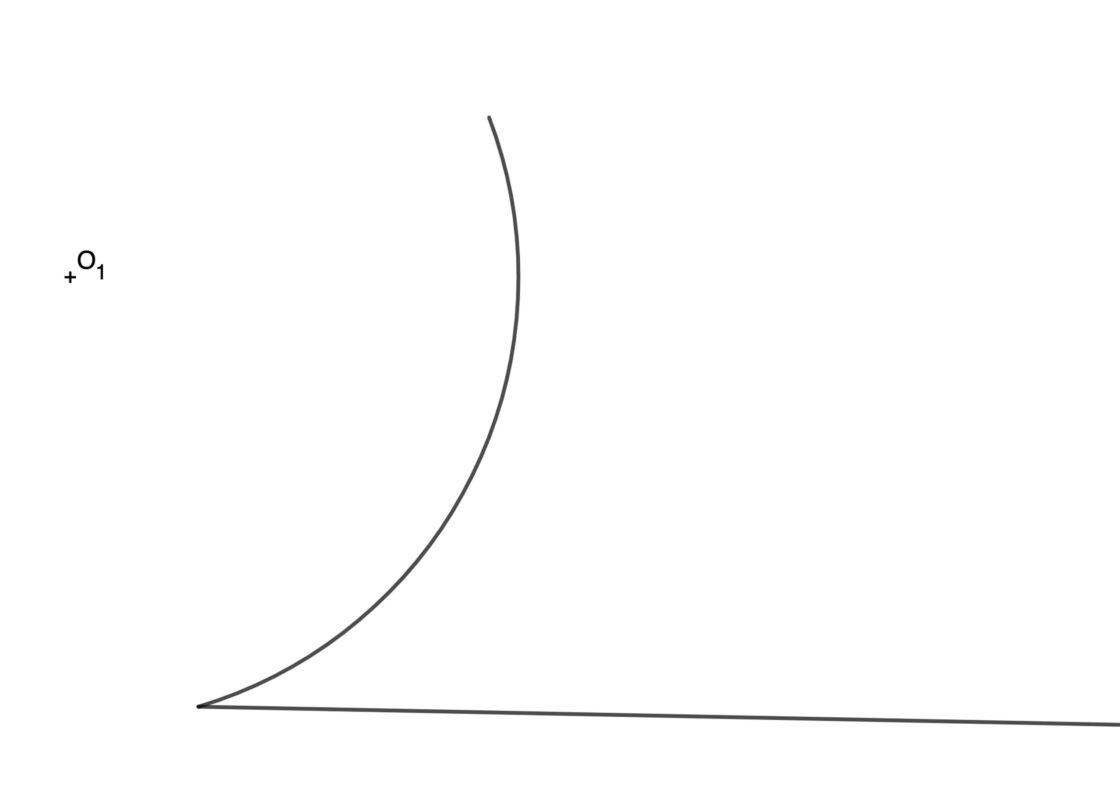
Como dato curioso, la bisectriz de un ángulo curvilíneo se corresponde con parte de una elipse. Aquí abajo tienes la demostración gráfica, para que puedas comprobarlo.
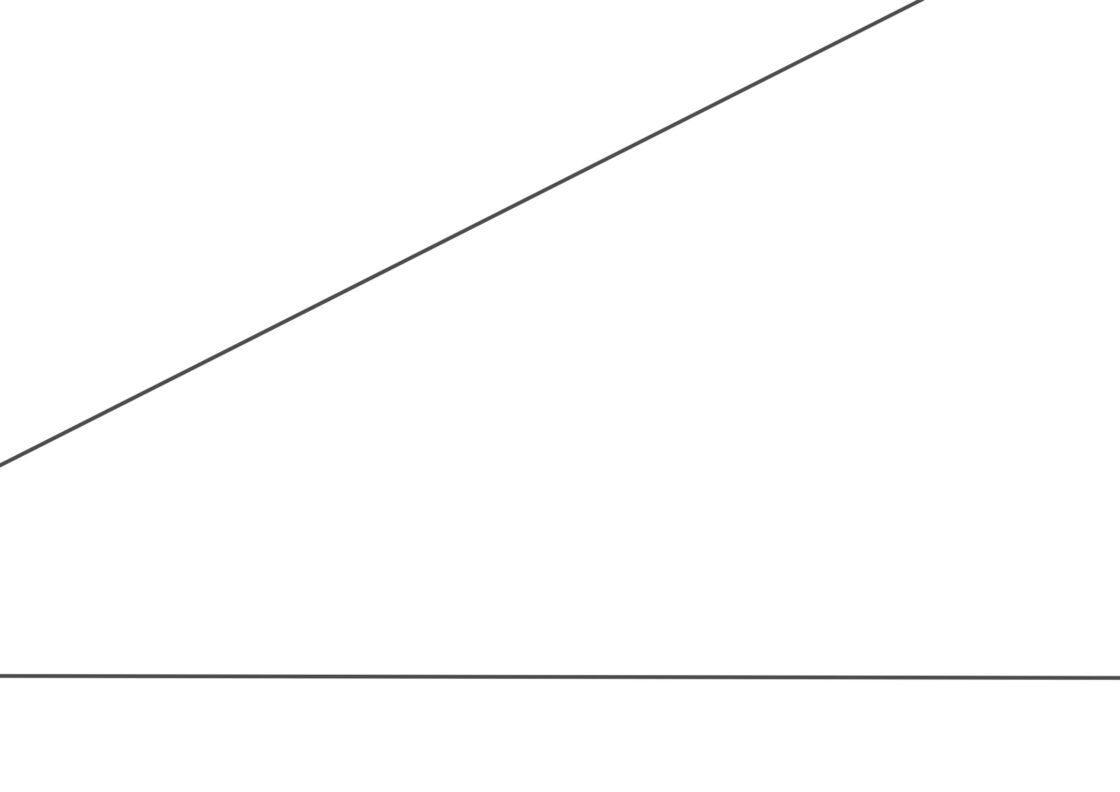
Bisectriz del ángulo mixtilíneo
Al igual que en el caso anterior, debemos recordar que cualquier punto de la bisectriz se encuentra siempre a la misma distancia de ambos lados. Tu punto de partida será similar a esto.
- En primer lugar, necesitamos realizar una perpendicular al lado recto. Da igual por donde la tracemos. Yo he marcado un punto arbitrario al que he llamado E
- Acto seguido trazamos un arco con una medida cualquiera que corta a ésta perpendicular en el punto M
- Con esa misma medida, repetimos la operación, marcando los puntos N y O
- Utilizando escuadra y cartabón (es mucho más rápido) dibujamos paralelas al segmento AB que pasan por los puntos M, N y O
- Dibujamos una recta cualquiera que pasa por D, la que yo he trazado corta al lado curvo en el punto P
- Utilizando la misma medida que usamos antes para encontrar los puntos M, N y O, realizamos varios arcos en la recta auxiliar que acabamos de dibujar, hayando los puntos Q, R y S
- Realizamos varias circunferencias, todas con centro en D y radio hasta Q, R y S
- El punto donde se cortan la circunferencia de radio DQ y la paralela que pasa por M nos marca el primer punto de la bisectriz. Los demás puntos se obtienen de los puntos de corte, siguiendo la secuencia lógica. Primera paralela con la primera circunferencia, la segunda paralela con la segunda circunferencia y así sucesivamente
- Uniendo todos esos puntos de corte, que en mi caso se llaman T, U y V, obtenemos la bisectriz del ángulo mixtilíneo.
En este caso, la bisectriz de unn ángulo mixtilíneo es una parábola. En la aplicación de aquí abajo lo puedes comprobar moviendo el punto B.
Bisectriz de ángulos que se cortan fuera del plano
En todos los ejemplos anteriores hemos visto ángulos cuyo vértice se encuentra dentro del plano. Pero… ¿Qué pasa cuando no vemos el vértice? ¿Podemos hallar la bisectriz de un ángulo cuyos lados se cortan fuera del plano? Tu punto de partida se parece a esto.
La respuesta es si, y es mucho más sencillo de lo que podrías imaginar. Básicamente el proceso se reduce a trazar paralelas a los lados del ángulo. A la misma distancia de los lados, eso si. La bisectriz del nuevo ángulo también será la bisectriz del ángulo que conocemos.
