Vamos a empezar definiendo lo que es el arco capaz. Técnicamente se define como el lugar geométrico de los puntos del plano desde los cuales se puede observar un segmento concreto desde un ángulo α
Básicamente es un arco que empieza y acaba en el segmento, y cualquier ángulo que hagamos, desde cualquier punto del arco, hacia los extremos del segmento, tendrá siempre el mismo valor.
- Debemos empezar trazando una perpendicular por uno de los extremos del segmento (da igual cual). Yo voy a optar por el método más sencillo, mediante una recta auxiliar.
- Prolongamos el segmento hacia uno de los extremos (yo he escogido el B).
- Con centro en B y un radio cualquiera trazamos dos arcos de circunferencia (con la misma medida) que cortan al segmento y a la recta auxiliar en los puntos F y G
- Realizamos dos arcos (de igual medida) desde F y G teniendo cuidado de que la medida sea lo suficientemente grande como para que se corten en los puntos I y J
- Uniendo los puntos I y J tenemos la perpendicular.
El siguiente paso consiste en trasladar el ángulo a la perpendicula que acabamos de realizar. Vamos a ver como.
- Con centro en el vértice del ángulo y un radio cualquiera, trazamos un arco que corta a ambos lados del ángulo en dos puntos. En este caso nos interesa el punto K y su distancia al vértice.
- Usamos esa misma distancia para dibujar un arco con centro en B que corta a la perpendicular en el punto L
- Ahora trazamos un arco con centro en K y radio hasta el otro punto de corte del ángulo, que hemos llamado M
- Utilizando esa misma medida, y con centro en L, vamos a dibujar un arco que corta al arco que parte de L en el punto N
- Dibujamos la recta que une B y N. Esta recta define lo que sería el ángulo resultante de restar al ángulo de 90º el ángulo α
Ya casi está, ahora tenemos que trazar la mediatriz del segmento AB y ver donde corta a la recta anterior.
- Con una distancia cualquiera trazamos un arco con centro en A, y con la misma medida, pero centro en B, vemos donde se cortan, obteniendo los puntos P y Q
- Unimos los puntos P y Q, hallando así el punto R
- Para finalizar trazamos un arco con centro en R, y distancia hasta A (ó B), encontrando así la solución que estamos buscando.
En la aplicación de aquí abajo puedes mover el punto D para comprobar que la construcción es siempre correcta, de manera independiente al ángulo inicial.
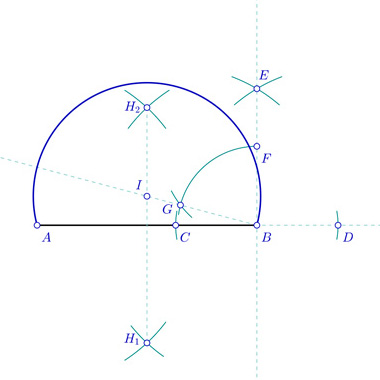
A continuación te pongo una variante para hallar el arco capaz que también es válida. La diferencia es que se desarrolla hacia abajo. Habrá momentos en los que sea muy útil, en especial si la parte donde vas a dibujar el arco capaz ya tiene más trazados hechos. No obstante, por lo general es preferible usar el primer método, ya que es más preciso y el resultado queda más compacto.
- Empieza por situar el ángulo que te proporcionan con el vértice en A ó B, y dibuja su lado. En éste ejemplo yo lo he dibujado a partir de A.
- Traza una perpendicular al lado del ángulo que acabas de dibujar, que pase por el vértice del ángulo. En este caso, tiene que pasar por A.
- Ahora dibuja la mediatriz del segmento AB. Donde esa mediatriz corta a la perpendicular que dibujaste antes, tienes el punto O, que es el centro del arco capaz que estás buscado.
- El arco capaz que buscas lo hallas pinchando en O y usando de radio la distancia entre O y el punto A (o el punto B)
Aquí abajo puedes mover el punto P para variar el ángulo. También puedes mover el punto C para verificar que la construcción es correcta.
Dados dos segmentos AB y BC, hallar los puntos desde los que se ven desde un ángulo dado
Este problema es sencillo, pero metódico y repetitivo. Consiste en hallar el arco capaz de ambos segmentos, tanto en una dirección, como en otra. Luego solo tienes que marcar los puntos donde se cortan, que serán la solución buscada.
En la aplicación inferior puedes modificar el punto D para variar el ángulo, y los puntos A y B para modificar los segmentos. Los puntos E y F son la solución buscada.
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti. Gracias de antemano por dejar tu comentario un poco más abajo.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
