En los ejercicios con ángulos debemos pensar siempre que estamos trabajando con triángulos. Al usar el compás para resolver problemas de suma, resta y traslación de ángulos, en realidad lo que estamos haciendo es copiar medidas de un punto a otro para mover triángulos.
Tipos de ángulos
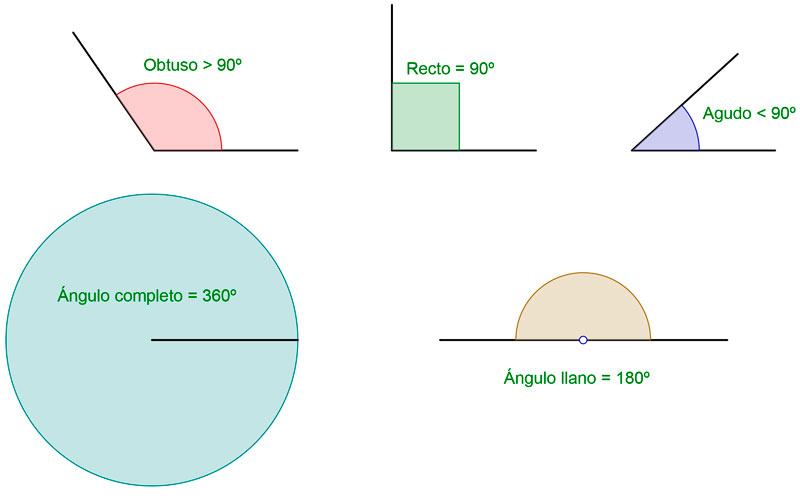
Vamos a empezar explicando los diferentes tipos de ángulos:
- Agudo: Mide menos de 90 grados.
- Recto: Mide 90 grados.
- Obtuso: Cuando mide más de 90 grados.
- Llano: Si mide exactamente 180 grados.
- Completo: Si mide 360 grados.
Por otra parte, también podemos decir de ellos que son convexos si miden menos de 180 grados, y cóncavos, cuando miden más de 180 grados (y menos de 360).
¿Como referirse a ellos?
Se suelen nombrar con una letra griega α, β, γ
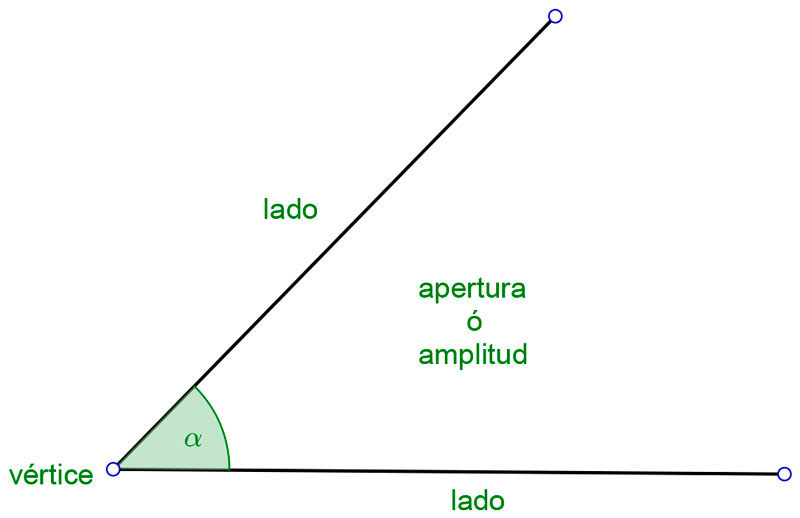
Las distintas partes del mismo son: vértice, lado y apertura o amplitud.

Denominación de los ángulos según su posición
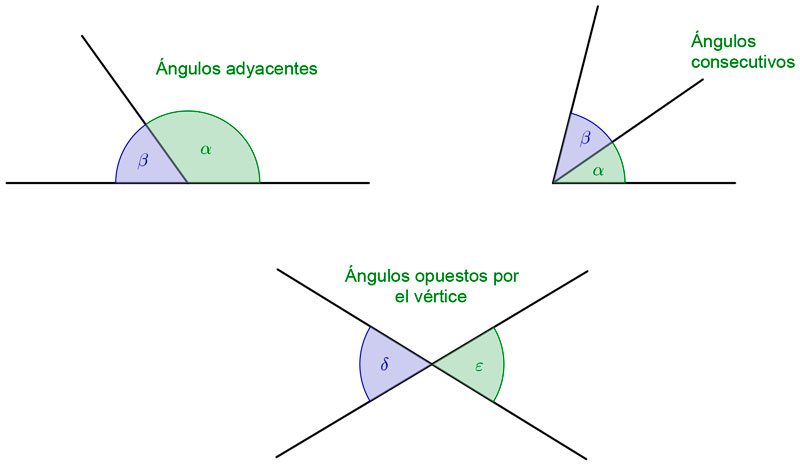
Dependiendo de como se encuentren situados, se llaman de tres maneras respectivamente:
- Consecutivos: Cuando comparten el vértice y uno de los lados.
- Adyacentes: Si la suma de ambos es 180º
- Opuestos por el vértice: Los lados de uno de los ángulos son la prolongación de los del otro, y comparten solo el vértice.
Según su suma con otro ángulo se llaman…
Hay que tener en cuenta que un ángulo se puede llamar de varias maneras a la ver. En éste caso vamos a ver como se denominan cuando se suman entre si.
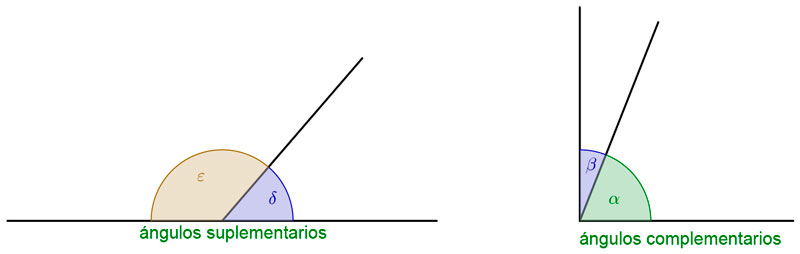
- Complementarios: Cuando entre los dos suman 90º
- Suplementarios: Si al sumarlos dan 180º
Operaciones con ángulos
La más básica y fácil, y que además necesitaremos para poder realizar la suma y la resta, es la operación de traslación. Es decir, mover un ángulo de un lado a otro.
Traslación de ángulos
Voy a resumirlo de forma muy rápida, y en el vídeo de abajo podéis ver el proceso paso por paso. Para éste ejemplo, vamos a suponer que queremos mover el ángulo α para que su vértice coincida con el punto A y uno de sus lados sobre el segmento AB. Tu punto de partida será algo parecido a esto:
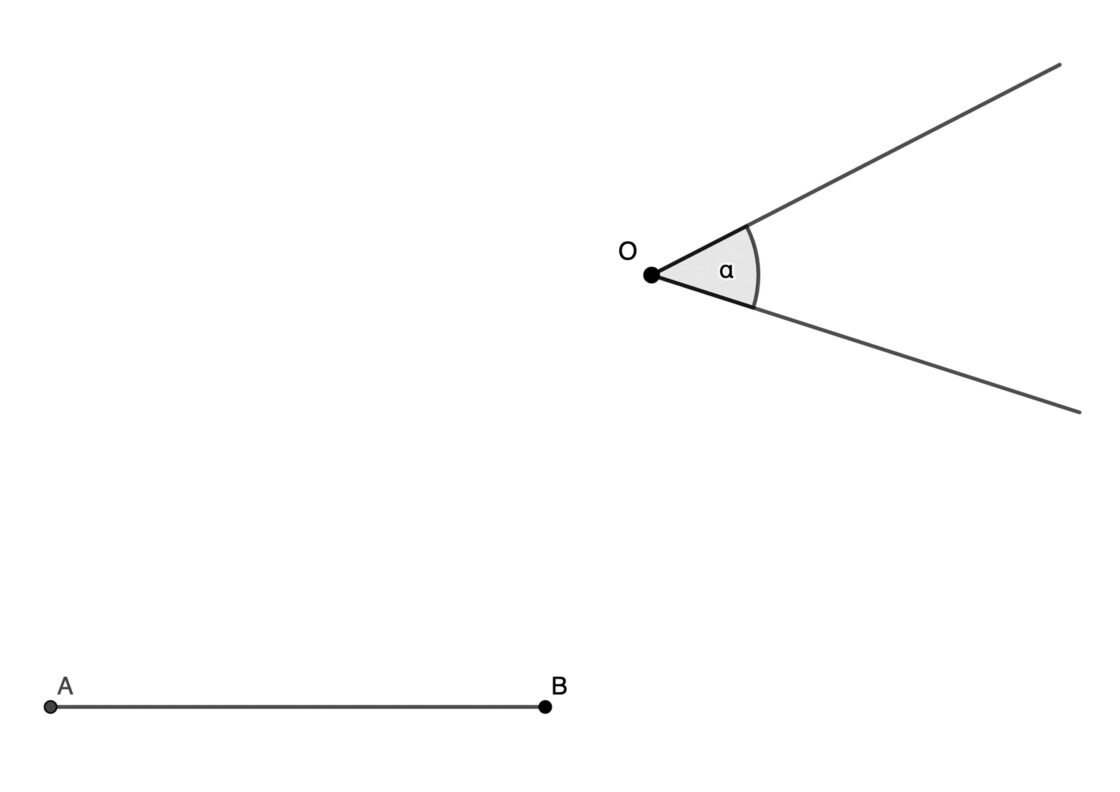
- Trazamos una circunferencia con un radio cualquiera y centro en el vértice O de α cortando a los lados en dos puntos que llamaremos C y D
- Llevamos esa misma distancia a partir del punto A, hallando el punto E
- Con centro en C trazamos un arco hasta D con el objetivo de conocer esa medida.
- Con centro en E trazamos un arco que corta al arco que hemos trazado antes en F
- Y ya está. Si unimos los puntos A y F obtendremos el ángulo que estamos buscando.
Aquí abajo puedes mover los dos puntos azules sin nombre para ver que el proceso sigue siendo válido de forma independiente al ángulo que sea.
Suma de ángulos
El proceso es prácticamente el mismo que el anterior. Tan solo nos vamos a limitar a mover un ángulo de manera que quede consecutivo a otro. Tu punto de partida es similar a este:
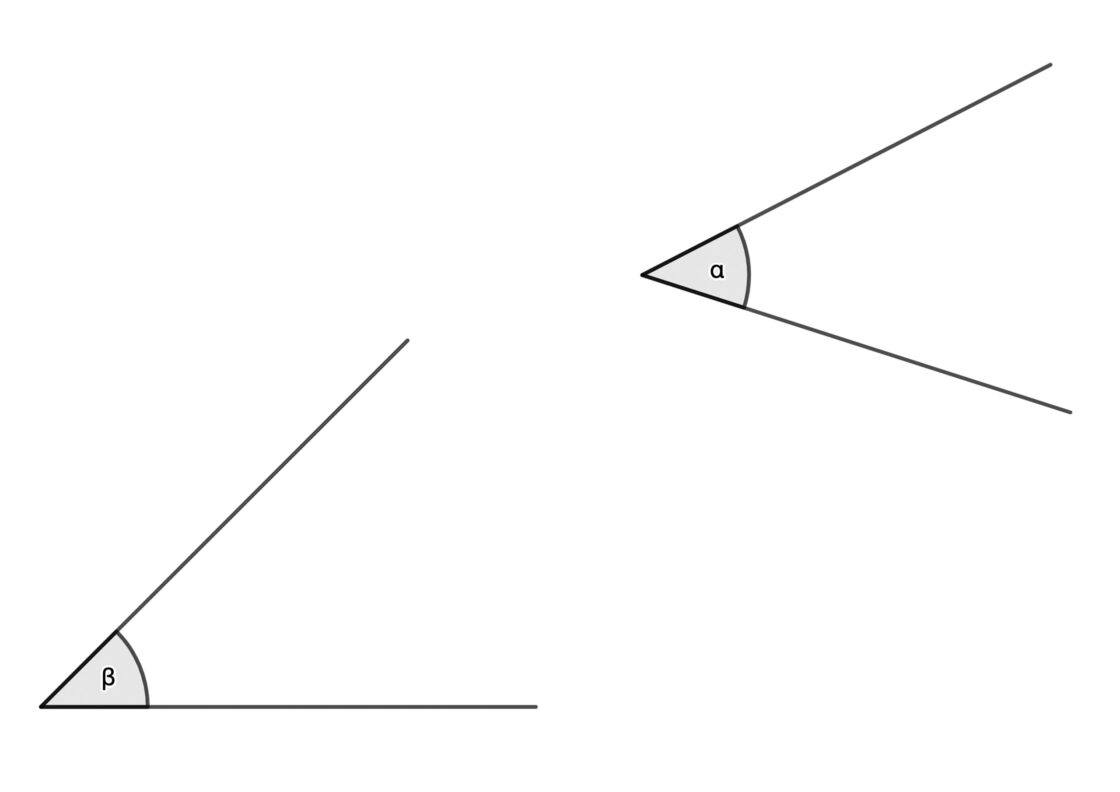
- Con centro en el vértice de α y una medida cualquiera, trazaremos un arco que corta a los lados del ángulo en dos puntos que llamaremos F y G
- Llevamos esa misma distancia sobre el lado que usaremos de referencia, hallando el punto H
- Trazamos un arco de circunferencia con centro en F hasta G
- Nos llevamos esta misma medida, con centro en H y cortamos al arco que hemos dibujado antes en I
- Y ya lo tenemos, uniendo el vértice de β y el punto I ya tenemos la suma de ambos ángulos.
Cómo restar ángulos
Como vais a ver a continuación, el proceso es exactamente el mismo que en el caso anterior. La única diferencia es que en vez de hacer el traslado hacia el exterior, lo haremos hacia el interior del ángulo. El punto de partida será algo parecido a esto:
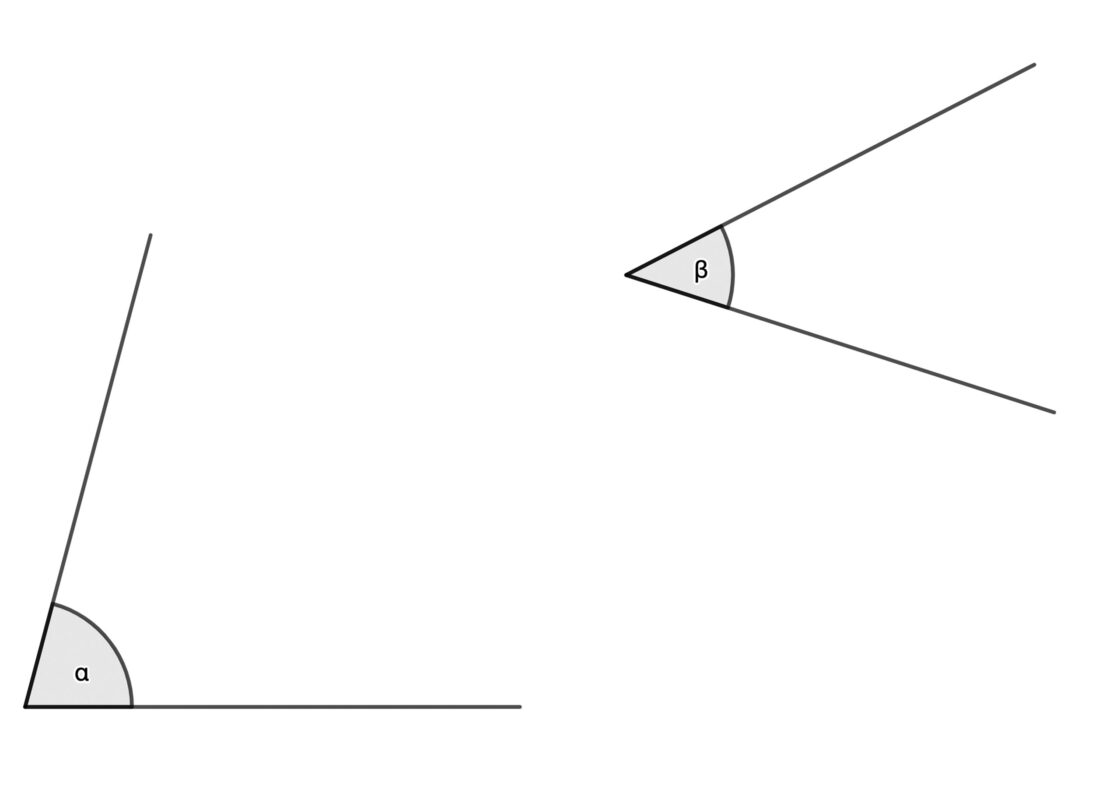
- Con centro en el vértice de β y un radio cualquiera trazamos un arco que corta a los lados de β en F y G
- Con esa misma distancia, y centro en el vértice de α trazamos un arco que corta a uno de los lados del ángulo α en H
- Dibujamos un arco con el compás desde F a G
- Utilizando esa misma distancia, y con centro en H realizamos un arco que corta al arco que hemos dibujado antes en I
- Ya lo tenemos, uniendo el vértice de β con el punto I tenemos el ángulo β, y por tanto el ángulo que queda es la resta de ambos.
Dibujar el ángulo de 15º, 30º, 45º… con compás
Estos problemas son relativamente comunes de encontrar, algunos de ellos tienen varias posibles soluciones. Yo os voy a poner aquí la más fácil de todas. Los ejercicios los he ordenado de más fácil a más difícil.
Dibujar un ángulo de 90 grados
Si ya sabes dibujar perpendiculares por un extremo de un segmento, ya sabes dibujar el ángulo de 90º, porque cualquier perpendicular forma un ángulo de 90º con la recta que corta.
Dibujar un ángulo de 60 grados
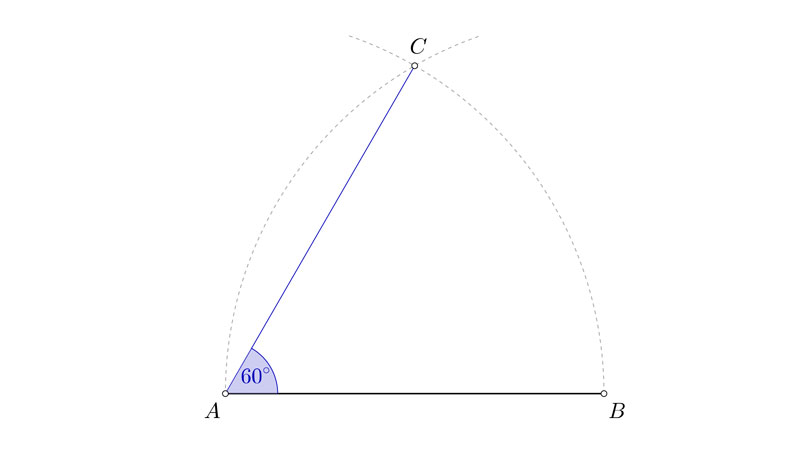
Dibujar un ángulo de 45 grados
¿Recuerdas como se halla la bisectriz de un ángulo? Pues para hallar el ángulo de 45 grados solo tienes que trazar la bisectriz del de 90 grados y ya lo tienes.
Dibujar el ángulo de 30 grados
¿Recuerdas como se hallaba el ángulo de 60 grados? Pues para hallar el de 30 grados lo único que tienes que hacer es trazar su bisectriz… ¿Y si quieres uno de 15 grados? Pues una vez tengas el de 30 grados vuelves a trazar la bisectriz. ¿Sencillo, verdad?
Una vez tengamos el de 15 grados, podemos hallar cualquier ángulo que sea múltiplo suyo. Por ejemplo, el de 105 sería el de 90+15. También podemos utilizar múltiplos del de 30 ó de 45. Por ejemplo, el de 120 será el de 90+30 o dos de 60.
